核电主管道用钢316LN高温变形性能研究

潘品李 钟约先 马庆贤 袁朝龙 朱思阳

清华大学先进成形制造教育部重点实验室，北京，100084

0 引言

核电站主管道是核电蒸汽供应系统输出堆芯热能的“大动脉”，是核电站的核一级关键部件之一。AP1000技术为第三代核电技术，其设计寿命提高到60年，核电站安全性能指标也大幅度提升，其主管道要求整体制造，难度很大。主管道用钢为316LN超低碳控氮奥氏体不锈钢，该钢种塑性差、变形抗力大，无法通过热处理细化晶粒，而其最终产品晶粒度要求应达到ASTM2级或者更细（ASTM4级）［1－2］。因此，主管道实心轴坯的锻造过程对细化晶粒有着至关重要的影响。

低层错能的金属材料在热塑性变形过程中，动态再结晶是其主要的软化机制。动态再结晶是以无畸变的晶核生成、长大形成再结晶晶粒代替含有高位错密度的形变晶粒的过程，在消除大量位错的同时达到晶粒细化的目的。20世纪60年代以来，以加拿大的McQueen和英国的Sellars为代表的各国学者研究了高温塑性变形中的软化机制，采用Zener－Hollomon参数来描述金属的流动行为，对工艺参数和软化机制之间的关系进行了研究，并研究了动态再结晶和静态再结晶的晶粒变化模式。在此基础上，Sellars、Yada、Roberts等学者对热加工过程的组织演化规律进行了研究，通过实验建立了一些特定金属的动态再结晶、静态再结晶模型和晶粒长大模型［3－4］。

本文通过热模拟实验，研究并建立了316LN钢的动态再结晶模型，为制定合理的工艺，控制产品性能提供了理论依据，为建立316LN钢锻造生产过程的数值模拟模型提供了重要基础。本实验用钢取自电渣重熔钢锭，与真空浇铸钢锭相比，具有以下优点：钢中夹杂物细小、弥散，氧、硫含量极低；钢的均匀性高，锻件纵横向性能差异很小，锻件热塑性高［5］。

1 热模拟实验方案

实验所用316LN钢主要化学成分（质量分数）如表1所示，符合ASME SA－376中对于该材料化学成分的规定。实验设备为Gleeble1500热模拟实验机。实验采用平面压缩法，试样为φ6mm×10mm的圆柱。实验工艺流程如下：先将试样以5℃/s的速度加热至1100℃并保温3min，使得试样的初始晶粒度一致，再以10℃/s的速度将温度调整至变形温度t，保温1min，然后压缩试样变形至真实应变ε＝0.7（变形程度为50%），最后水冷淬火以保留试样高温变形下的显微组织。工艺参数如表2所示。

表1 316LN钢主要化学成分（质量分数） %

表2 实验工艺参数设计

2 实验数据处理和分析

2.1 316LN钢高温流动应力曲线

316 LN钢在变形温度为900～1200℃，变形速率为0.01～1s－1条件下的流动应力曲线如图1所示。

由图1可见，应变速率较低且温度较高时，316LN钢发生了连续动态再结晶，随应变增加应力值基本恒定。应变速率较高时，316LN钢只有在较高温度下变形才能发生动态再结晶；温度较高时，各应变速率下都很容易发生动态再结晶。在锻造工艺参数内，提高变形温度和降低应变速率，均有利于减小316LN钢的峰值应力，使之发生动态再结晶。应变速率为0.01s－1，变形温度从1200℃降至950℃时，峰值应力稳步增大；而当温度降至900℃时，峰值应力明显增大，如图1c。这和工厂实际生产情况相当吻合，即当温度降至900℃时，锻造时变形抗力很大，水压机几乎锻不动。因此建议在进行大型核电主管道锻造时，锻造温度控制在900℃以上（建议950℃）为宜。大型核电主管道锻造时应变速率可达0.01s－1数量级，所以得到的数据对工厂实际生产有很大的参考价值。

2.2 动态再结晶热激活过程模型

变形温度和变形速率对金属的动态再结晶都起作用，两者共同决定了材料变形过程中是否发生动态再结晶。二者之间的等效关系可以用温度补偿应变速率Zener－Hollomon参数来表述：

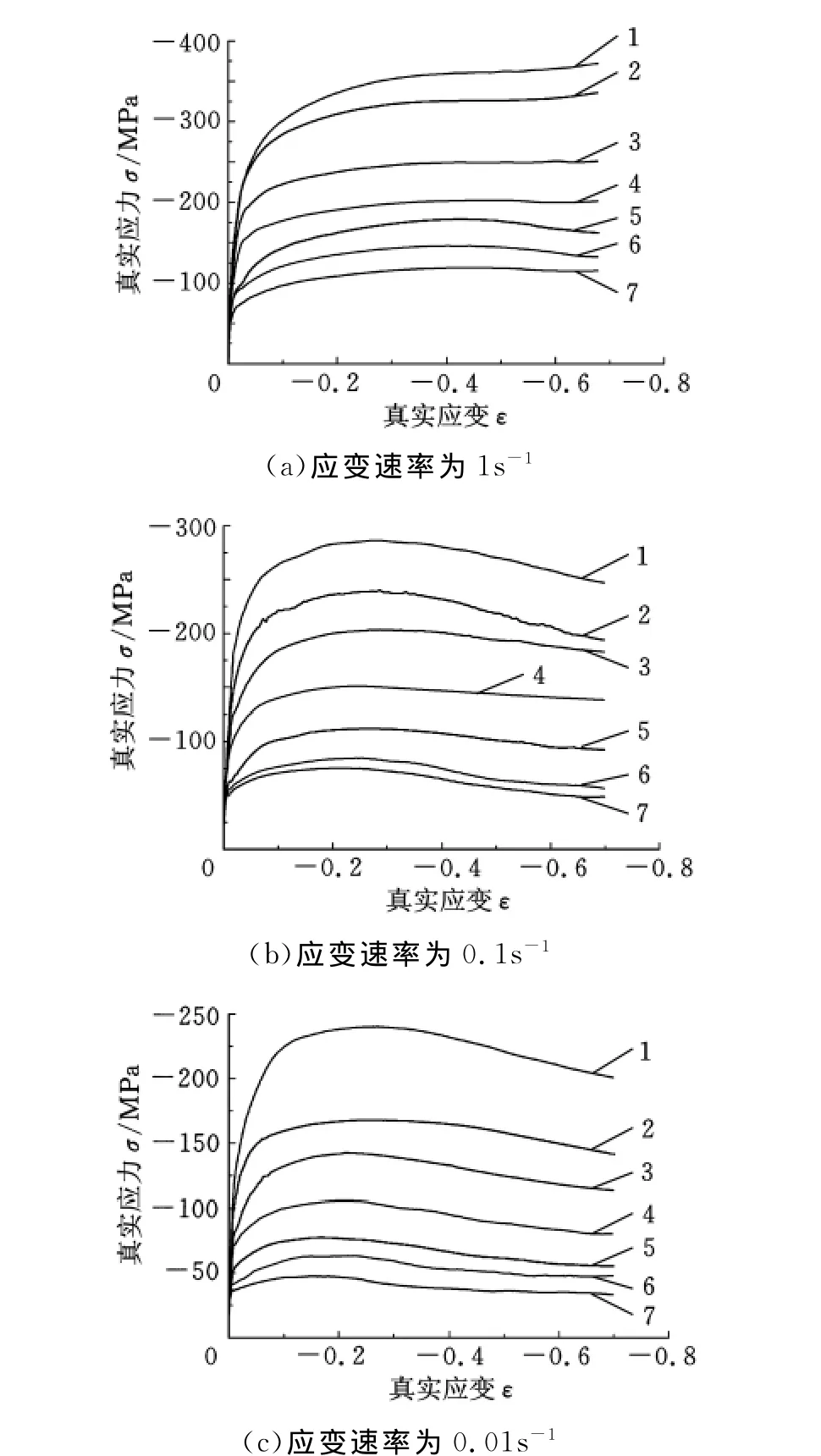
图1 316LN钢流动应力曲线

式中，为应变速率；QDRX为变形激活能；R为气体常数；T为绝对温度；A和n为只与材料自身相关的常系数；σp为第一个流动应力峰值。

将实验数据代入式（1）进行多元线性回归，可得316LN钢动态再结晶热激活模型（相关系数R＝0.985 34）：

参数Z可以作为判定是否发生动态再结晶的依据，其上限Zmax为应变速率较大、变形温度较低时，材料中由于变形积聚了一定数量位错，但是由于发生动态再结晶的形核需要一定的时间，过快的变形速率使得孕育时间不够；其下限Zmin为应变速率很低、变形温度较高时，过高的变形温度导致不能积聚起足够数量的变形储能结果。参数Z在两个极值之间时，随着变形量的增大将会依次发生动态回复、部分动态再结晶和完全动态再结晶。

将热模拟试样淬火，以保留高温变形结束瞬间的奥氏体晶粒组织。通过对热模拟试样显微组织的观察，可知应变速率为1s－1、温度未达到1000℃时，完全不发生动态再结晶，此时动态回复是其主要的软化机制，其典型的显微组织为沿变形方向拉长的晶粒，如图2a所示。当温度达到或超过1000℃时，发生部分动态再结晶，其典型的显微组织为原奥氏体周围沿晶界产生了许多细小等轴晶粒，1200℃条件下的试样显微组织如图2b所示。该应变速率下没有发生完全动态再结晶。应变速率为0.1s－1、温度为900℃时发生动态再结晶，1100℃可达稳态，即发生完全动态再结晶，其典型的显微组织为细小的等轴晶粒，如图2c所示。应变速率为0.01s－1、温度达到900℃时发生动态再结晶，1050℃可达稳态。

图2 不同变形温度和变形速率条件下的试样显微组织

根据316LN钢动态再结晶热激活模型，计算各个工艺参数下的参数Z，可得图3所示的变形温度、变形速率与参数Z的关系，其中横坐标的物理意义如表3所示，表中1～21为不同工艺参数所对应的序号。

图3 变形温度、变形速率与参数Z的关系

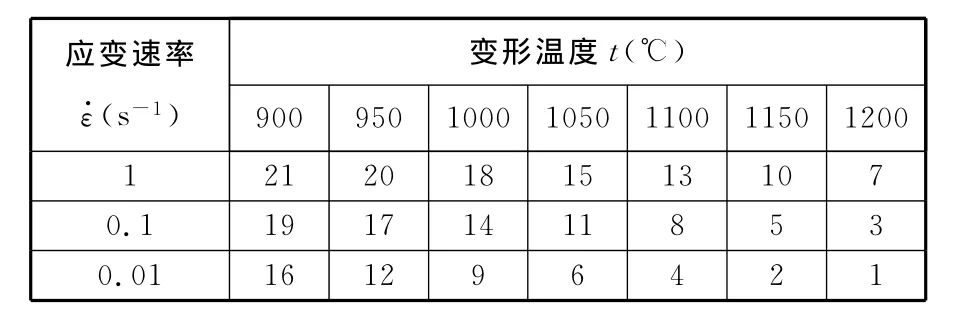
表3 不同变形温度和变形速率所对应的序号

由图3可知，lnZ的走势以及所对应的各个工艺参数完全吻合显微组织的结论，即在给定的变形量条件下（本文实验为真应变0.7），存在一个动态再结晶发生与否的分界点Zmax，参数Z大于Zmax时，变形过程中材料不能发生动态再结晶，如序号20、21；小于Zmax时，变形过程中材料可以发生动态再结晶，如序号1～19。但由于实验条件的限制，未能测出参数Z的下限值Zmin。

2.3 动态再结晶动力学模型

应变量ε决定了材料在变形过程中处于哪个阶段（动态回复、部分动态再结晶和完全动态再结晶）。金属材料发生动态再结晶时，其特征应变（峰值应变εp、稳态应变εs、临界应变εc）和参数Z之间存在的关系，以及动态再结晶发生的初始临界应变εc与峰值应变εp之间存在的关系分别为

式中，Bi和m为只与材料自身相关的常系数，i∈（p，s，c）。

将实验数据代入式（2）、式（3）进行多元线性回归，可得316LN钢动态再结晶动力学模型：εp＝0.0519Z0.0442，相关系数R＝0.984 12；εc＝ 0.8εp；εs＝ 0.1532Z0.0444， 相 关 系 数R＝0.984 44。

结果表明，lnεc、lnεs与lnZ之间分别存在图4所示的线性关系。图4中的lnεc与lnZ关系直线和lnεs与lnZ关系直线将参数Z和应变ε组成的平面分为3个部分：Ⅰ区域应变小于εc，该区域的参数Z及应变条件不足以积累足够的位错密度，达到动态再结晶所需的应变能，不能发生动态再结晶；Ⅲ区域应变大于εs，可发生完全动态再结晶；位于两者之间的Ⅱ区域，可发生部分动态再结晶。相同参数Z条件下，可增大应变量诱使动态再结晶发生；相同应变量条件下，可调整参数Z来控制动态再结晶的发生。

图4 316LN钢临界应变、稳态应变与Z参数的关系

由金相显微组织分析可知，工艺序号1～6和8分别发生了完全动态再结晶。根据316LN钢动态再结晶动力学模型，计算的7～14各个工艺参数下的εs值如表4所示。

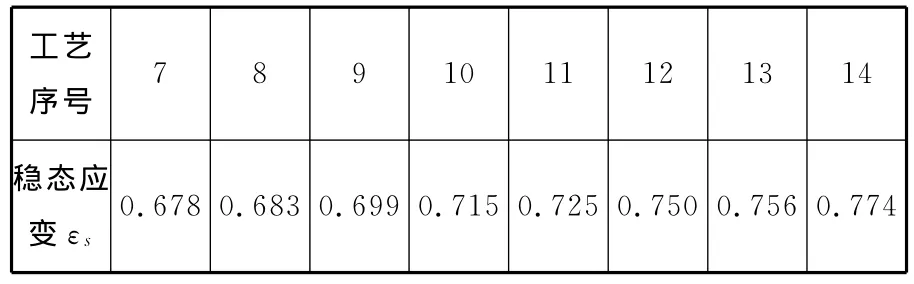
表4 不同工艺参数条件下的稳态应变值

由表4可看出，工艺序号7～9下发生了完全动态再结晶，工艺序号10～14下为部分再结晶，而由于实际实验设备的限制，工艺序号7～9下实际完成的真应变分别为0.676、0.699和0.697，从另一方面印证了动力学模型的正确性。

2.4 动态再结晶运动学模型

为了定量地描述金属材料发生动态再结晶的程度，一般采用Avrami型表达式描述其动态再结晶体积比例XDRX，即

式中，k和l为只与材料自身相关的常系数。

实验中为避免视场选择和金相腐蚀等人为因素影响，选用Beynon等［6］提出的基于高温流动应力曲线的金属材料动态再结晶体积比例测量方法计算XDRX。将实验数据代入式（4）进行多元线性回归，可得316LN钢动态再结晶运动学模型（相关系数R＝0.983 17）：

一定变形温度和应变速率条件下，当变形达到初始临界应变εc时发生动态再结晶，达到稳态应变εs时发生完全动态再结晶，介于两者之间发生部分动态再结晶。图5所示为不同变形温度和变形速率条件下试样显微组织，图5a和图5b分别为典型的部分动态再结晶组织，即在较大的原奥氏体晶界处形成再结晶核心，长大成为细小等轴晶粒。根据体视学和定量金相学，用截线法对图5a和图5b的动态再结晶体积比例XDRX进行测量，所得结果分别为73.94%和86.21%，根据动态再结晶运动学模型得到图5a和图5b的计算值分别为74.22%和86.78%，误差分别为0.38%和0.66%。图5c为完全动态再结晶组织，根据动态再结晶运动学模型得到的计算值为97.04%。上述图例足以验证动态再结晶运动学模型的准确性。

图5 不同变形温度和变形速率条件下的试样显微组织

2.5 动态再结晶晶粒尺寸模型

研究认为，动态再结晶发生后的晶粒尺寸dDRX与Z参数之间存在如下关系：

式中，D和j为只与材料自身相关的常系数。

将实验取得的结果试样腐蚀得到原奥氏体晶界，测量发生动态再结晶试样的晶粒平均尺寸，将结果和实验条件代入式（5）进行多元回归，可得316LN钢动态再结晶晶粒尺寸模型，相关系数R＝0.983 88，dDRX＝ 6.108×106Z－0.392。 由动态再结晶晶粒尺寸模型可知，参数Z越小，也即应变速率越低，温度越高，再结晶后的晶粒尺寸越大。

金属热塑性变形机理主要有晶内滑移、晶内孪生、晶界滑移和扩散蠕变。在通常情况下，晶内滑移是热变形的主要机理。高温时原子间距加大，原子的热振动和扩散速度加快，位错活跃，滑移、攀移、交滑移和位错结点脱锚比低温时容易；滑移系增多，交叉滑移灵便性提高，改善了各晶粒之间的变形协调性；同时在热变形状态下，晶界对位错运动的阻碍作用相对减弱，位错有可能进入晶界［7］。这样就使得高温时，杂乱分布的位错逐渐集中或按规律排列，动态回复的程度增大，从而减小了变形后的畸变能，使晶粒粗化。如图6所示，应变速率一定时，温度越高，发生完全动态再结晶后的晶粒尺寸越大。

同样地，变形速度很低时，金属在热塑性变形过程中产生的位错有足够的时间进行滑移、攀移、交滑移以及位错结点的脱锚，从而使得位错消失或者重新排列，位错以动态回复等其他软化方式消耗，从而由高能态的混乱排列向低能态的规则排列变化，减小了变形后的畸变能，使晶粒粗化。如图7所示，温度一定时，应变速率越小，发生完全动态再结晶后的晶粒尺寸越大。

图7 1200℃不同变形速率条件下的试样显微组织

当然，动态再结晶后的晶粒尺寸大小最终取决于变形温度和变形速率两个方面的因素。不同变形温度和变形速度下的动态再结晶后的尺寸大小可以相当（图8）。

用截线法分别计算出发生了完全动态再结晶后的晶粒尺寸，结果如表5所示。由表5可知，应变速率为0.01s－1时，在变形温度1050～1150℃范围内，再结晶后的晶粒尺寸维持在一个相对稳定的范围内；当温度上升为1200℃时，再结晶后的晶粒尺寸二倍于1150℃的晶粒尺寸，已经低于ASTM晶粒度4级（约为80.0μm）。当所用材料取自真空浇铸钢锭时，其在应变速率为0.01s－1、真应变为0.7时，发生完全动态再结晶后的晶粒尺寸如表6［8］所示（其中d0为原始晶粒尺寸）。对比表5和表6数据可以发现，在1050℃和1100℃条件下再结晶后的晶粒尺寸基本一致；但在1150℃条件下的动态再结晶对电渣重熔钢锭晶粒细化效果更好；而在1200℃下却得出相反的结论。建议在进行大型核电主管道锻造时（使用钢锭为电渣重熔钢锭），锻造温度控制在1200℃以下（建议1150℃）为宜。

图8 不同变形温度和变形速率条件下的试样显微组织

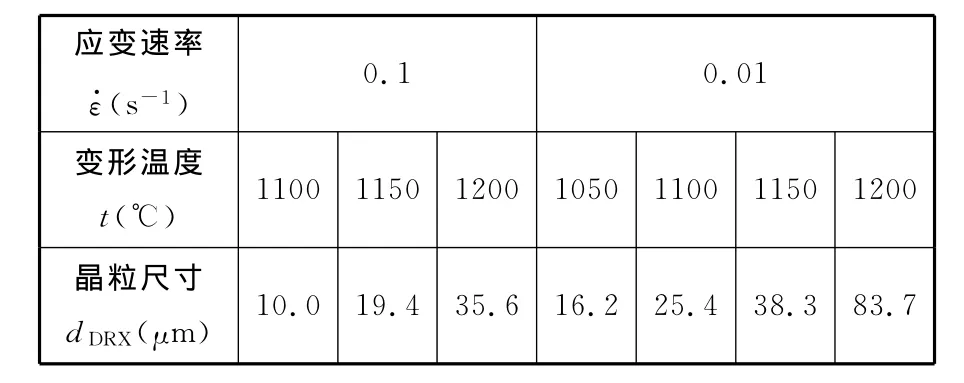
表5 不同工艺条件下的316LN钢发生完全动态再结晶后的晶粒尺寸

表6 应变速率为0.01s－1、真应变为0.7时的稳态晶粒尺寸

当动态再结晶完成后，积累的位错畸变能随之得以释放，但随着变形的继续，动态再结晶形成的晶粒又承受新的变形，产生新的加工硬化，从而积累位错畸变能，开始新的软化过程，动态再结晶持续进行。故在奥氏体动态再结晶中晶粒尺寸不是完全均匀的（图6b、图6c）。大型锻件锻造加工比较费时，并且锻造成形后都要停放一定的时间，使新晶粒可以通过逐步相互合并长大而达到一个稳定的尺寸，出现均匀化。

3 结论

本文针对大型核电主管道晶粒细化问题，系统研究了主管道用钢316LN的动态再结晶行为，为通过锻造工艺解决大型核电主管道晶粒细化问题提供了模型依据，主要结论如下：

（1）316LN钢为典型低层错能钢，在再结晶温度线以上可以发生连续动态再结晶。提高变形温度和减小应变速率有利于降低316LN钢的峰值应力，使之发生动态再结晶。

（2）建立了316LN钢完整的动态再结晶数学模型，定量地描述了316LN钢动态再结晶行为的全过程。

（3）在动态再结晶参数范围内，降低变形温度和增大应变速率均有利于细化动态再结晶晶粒尺寸。

（4）综合锻造过程中的变形抗力及再结晶细化晶粒等影响因素，初步建议316LN电渣重熔钢锭在锻造过程中的应变速率控制在0.01s－1以下，温度控制在950～1150℃。

［1］潘品李，钟约先，马庆贤，等.大型核电主管道制造技术的发展［J］.锻压装备与制造技术，2011（1）：13－17.

［2］Klanica F，Rao G.APP－PL01－Z0－200Rev.3－2010Reactor Coolant Loop Seamless Forged and Formed Pipe Fabrication Specification［S］.Pittsburgh：Westinghouse Electric Company LLC，2010.

［3］McQueen H J.Development of Dynamic Recrystallization Theory［J］.Materials Science and Engineering，2004，387/389：203－208.

［4］McQueen H J，Imbert C A C.Dynamic Recrystallization：Plasticity Enhancing Structural Development［J］.Journal of Alloys and Compounds，2004，378（1/2）：35－43.

［5］向大林.大型电渣重熔值得注意的几个问题［J］.大型铸锻件，2011（1）：26－35.

［6］Beynon J H，Sellars C M.Modeling Microstructure and Its Effects During Multi－pass Hot Rolling［J］.ISIJ International，1992，32（3）：359－367.

［7］刘全坤.材料成形基本原理［M］.北京：机械工业出版社，2004.

［8］陈明明.316LN不锈钢锻造过程晶粒演变规律实验与模拟研究［D］.太原：太原科技大学，2010.