从一道电磁感应问题的几种解法谈平均值

王丽军

（北京师大良乡附中，北京 102488）

电磁感应的问题中有一道比较常见的题.如图1（甲）所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L＝0.5m，电阻R＝0.4Ω，导轨上停放一质量m＝0.1kg，电阻r＝0.1Ω的金属杆，导轨电阻不计，整个装置处于磁感应强度B＝0.5T的匀强磁场中，方向竖直向下，现用一外力F沿水平方向拉杆，使之由静止开始做匀加速运动，若理想电压表示数u随时间关系如图1（乙）所示.

（1）求金属杆运动的加速度大小；

（2）求第3秒末拉力的功率；

（3）若在第4秒末撤去外力F，则金属杆还能运动多远？

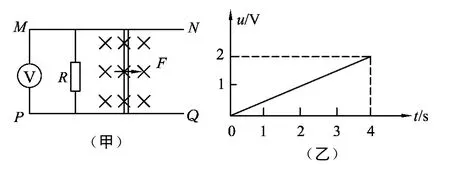
图1

前两问的比较简单在此不再赘述，只分析第三问.

过程分析1：根据前两问可以求出4s末金属杆的速度是v0＝10m／s，在撤去外力后，金属杆只受方向向左的安培力，金属杆将向右做减速运动直到静止.

在这个过程中，金属杆由于切割磁感线产生感应电动势为E＝BLv，回路中的感应电流为金属杆受到的安培力为F＝BIL，

可见随着金属杆速度的减小，安培力变小，加速度变小，速度随时间的变化不是均匀的（速度时间图像如图2所示），安培力随时间的变化也不是均匀的，所以这个过程中安培力对时间的平均值，其中F0是撤去外力瞬间的安培力.

图2

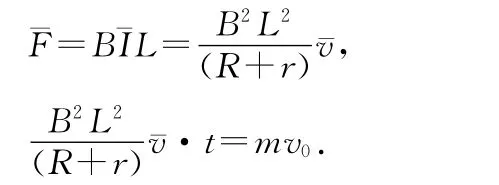
金属杆运动的距离x＝¯v·t，代入数据得x＝8m.

解法2：根据动量定理有¯F·t＝mv0，其中

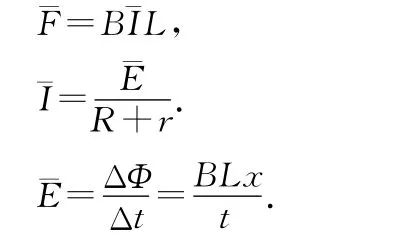
注意：上述两种解法中的平均值均为对时间的平均值.安培力对时间的平均值

过程分析2：通过上面的分析可知，由于速度随时间不是均匀变化所以导致感应电动势、感应电流、安培力随时间都不是均匀变化，那么速度随位移的变化是否是均匀的呢？

假设经过一段时间金属杆的速度从v0减速到v，金属杆的位移为x.

根据类似解法1和解法2的推导过程可知

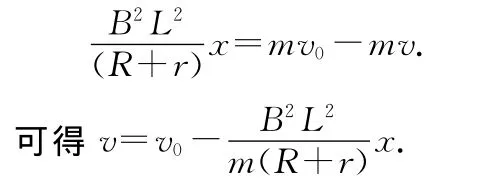
可以看出速度随位移的变化是线性变化，变化关系如图3.

即感应电动势、感应电流、安培力随位移均匀变化，此过程中安培力对位移的平均值

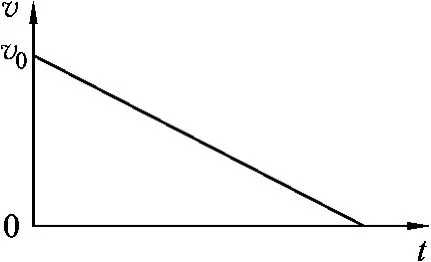
图3

注意：上述三种解法中有两个平均值，这两个平均值的平均的意义是不同的.

小结：关于两个平均值，一般说来，一个随时间变化的作用力F（t）作用在质量为m的物体上，经过一段时间t，物体速度从v1变化为v2.根据动量定理，有，则

同时，这个作用力也是随位移s而变化的，可记作F（s），在速度从v1变化为v2的过程中，发生位移s.根据动能定理，有

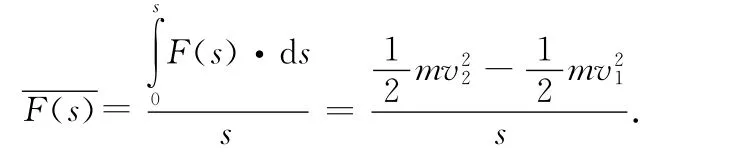
前者称为作用力对时间的平均值，后者称为作用力对空间的平均值，一般情况下，二者并不相等在特殊情况下，满足一定条件，二者可以相等.

所谓“当作恒力处理”，就是把一个变力作用的过程等效为大小等于它的平均力的恒力作用的过程，这里涉及到是哪个平均力的问题.应用动量定理应该是指对时间的平均力，应用动能定理应是指对位移的平均力，而同一个变力对时间的平均与对空间位移的平均一般不相等，一定要区分清楚.

除了上面的3种解法外还可以用积分的办法.

解法4：设某时刻金属杆的速度为v，经过很短的时间dt，金属杆的位移为dx，有

设初速度方向为正，有

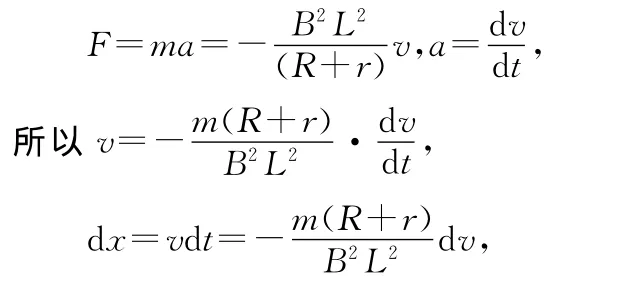
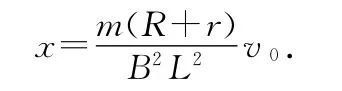
代入数据得x＝8m.

一般情况下，当我们说某个量的平均值，而没有说明是对什么的平均时，我们就默认为是对时间的平均值，例如我们说的“平均速度”、“平均功率”等等，都是指的对时间的平均值，也就是说，当我们说某个物理量对时间的平均值时，可以省略“对时间”这三个字.

同样，当我们要求某个过程中的平均作用力时，我们要理解为是对时间的平均，即而不能理解为后者必须称为“求这个过程中对空间位移的平均作用力”.当我们运用动量定理而求得的平均作用力是对时间的平均力，而我们运用动能定理求得的平均作用力则是对空间位移的平均力.