数字射线检测技术专题（三）——成像过程基本理论

郑世才

（新立机器厂，北京 100039）

1 成像过程概念

从一般的概念理解，成像过程可以概括为，成像系统（包括成像设备、器材和技术）对输入作出响应给出输出的过程。图1给出了成像基本过程的示意图。也就是，被观察的物空间对象作为成像系统的输入，在像空间成像系统输出获得的图像。或者说，物空间被观察对象作为成像系统的激励信号，成像系统对激励信号响应，在像空间输出图像。

图1 成像基本过程的示意图

不同成像系统，由于设备、器材和技术等的差异，使成像系统具有不同特性，使成像过程具有不同特点，对输入信号产生不同的响应，导致输出图像质量不同。

在研究的不同成像系统中，一类系统在理论上称为线性平移不变系统，也称为线性空间不变系统，或简单地称为线性系统。简单说，线性平移不变系统具有的基本特性是：

（1）输入是多个信号线性和时，输出信号等于这些信号对应输出的和。

（2）当输入信号作坐标平移时，输出信号形式不变，仅是平移一定坐标。

很多实际的成像系统都是线性平移不变系统，或至少在局部成像区域内可认为是这样的系统。对这样的系统，输出信号与输入信号间将存在简单的关系。以下讨论的理论内容都是针对这样的成像系统。

2 成像过程的空间域分析

对于线性平移不变系统的空间域成像过程，可如下分析。

2.1 点扩散函数

实际的成像系统由于存在的各种性能不完善，得到的像总会产生某种程度的模糊。对于一个成像系统，其成像特性集中反映在其对点物体的成像。如图2，成像系统对一个脉冲状的点物体，得到的像一般呈现为具有一定分布的钟形像。这个具有一定扩展分布像的函数，称为成像系统的点扩散函数（或者称为成像系统的脉冲响应函数），图3是成像系统点扩散函数的典型样式。

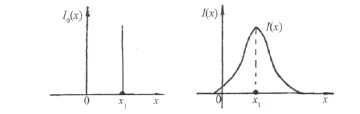
图2 点物体成像的扩散

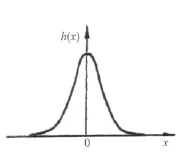
图3 成像系统的点扩散函数

在一维空间（包括对实际三维空间），点扩散函数一般记为h（x），缩写时记为PSF。成像系统性能不同，其点扩散函数不同。可以认为，点扩散函数集中反映了成像系统的成像特性。从下面的讨论可以看到，点扩散函数扩展宽度越小、分布形状越尖锐系统成像质量越好。

2.2 卷积成像过程

对于线性平移不变系统，按照点扩散函数概念，对于物空间的一个点I0（x1），经成像系统成像后，若成像系统的点扩散函数为h（x），则得到的像I（x）与物I0（x1）的关系为：

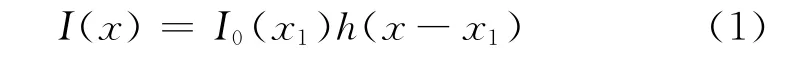
即，物空间一点经成像系统成像后，将按成像系统的点扩散函数扩展为一个区。在像分布的区中，不同点的幅度将是I0（x1）与点扩散函数h（x）在该位置点值的积。

任何物体，可看成由一系列点组成（不同点具有不同分布强度）。因此，线性平移不变成像系统对某物体成像时，应是各个点像的迭加和。如图4所示，这时像的任意点，实际将是一定范围内不同点的迭加结果。当把一个小区域Δx看成一点时，在某点xi处的像则可写成：

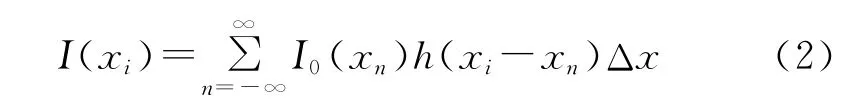
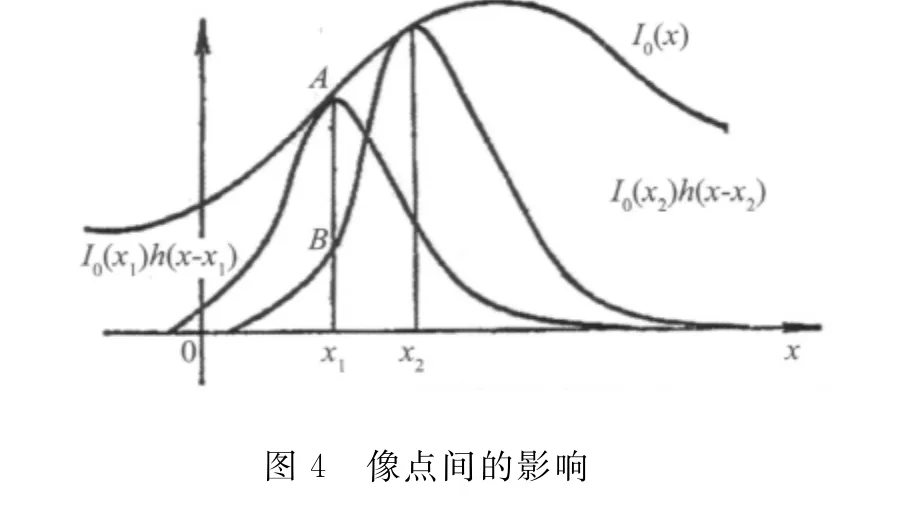
一般地，对于连续分布物体，可写成积分形式：

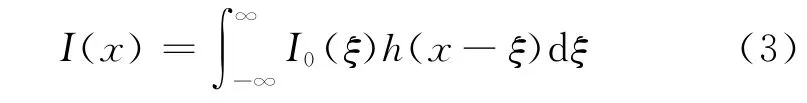
式中ξ为积分变量。此式在数学上表示的是，函数I（x）等于函数h（x）与函数I0（x）的卷积，卷积可用下式和符号“＊”表示：

由于卷积满足交换律，所以此式也可写为：

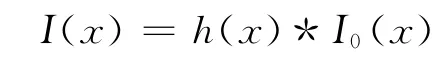
图5给出的是某成像系统对正弦信号的卷积成像过程。成像系统的点扩散函数为一矩形函数，图中画出了系统的点扩散函数和正弦信号的卷积过程，也可看出像点间相互影响的情况。它显示了成像系统的点扩散函数，表征成像系统成像特性的情况。

图5 卷积成像过程

2.3 成像过程的一般表示

对上述讨论一般化，这时线性平移不变系统的成像过程可按图6所示概括。记输入物函数为f（x），成像系统的点扩散函数为h（x），输出图像为g（x），则它们之间的关系为：

用卷积运算符号则可写成：

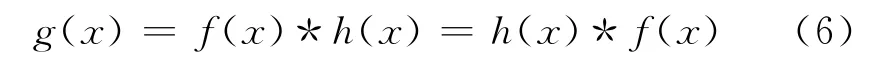
即，在空间域分析成像规律时，成像是物函数与成像系统的点扩散函数的卷积过程，成像质量决定于成像系统的点扩散函数。

因此，只要清楚了成像系统的点扩散函数，就可通过卷积运算给出成像系统对任何物体的输出图像，可确定成像系统对任意物体的成像情况。按卷积运算过程，成像后图像中的某点实际是一个区域中像的迭加。某点的像将受周围一定范围内像点的影响。

3 成像过程的空间频域分析

在空间频（率）域，可进一步分析成像系统的成像过程，可以看到成像系统成像过程更多的特点，可以对成像系统、成像过程、成像质量特征作出更清晰描述。

3.1 空间频率与调制度概念

类似于时间频率概念，对在空间按周期重复分布的对象引入空间频率概念。一般地，对在空间周期分布的信号，可采用图7描述。这时，空间分布信号的重复间距（图中p）称为空间周期，单位一般用mm，单位距离内所含的周期数则称为空间频率。空间频率常是单位距离内所含的线条与空隙对数，即“线对数”表示，单位一般用“Lp／mm”。空间频率若记为v，则其与空间周期p的关系为：这与时间频率中的关系相同。应用时，空间频率的意义常是一个细节在空间域的重复频率。

图7 空间频率概念

对一信号可引入调制度概念。调制度一般记为M，按图7所示符号，调制度概念定义为：

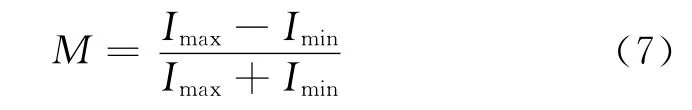
式中Imax为信号的最大值；Imin为信号的最小值。

从空间频率概念考虑，任何物体都可理解为包含着不同空间频率的组成部分。物体的轮廓、物体中的不同结构、物体中的细节（如存在的缺陷）等，按照它们的尺寸，可对应成不同空间频率。一般说，物体的轮廓部分形成空间频率的低频部分，物体的不同结构部分形成空间频率的中频部分，物体的细节（如存在的缺陷）部分形成空间频率的高频部分。

3.2 成像的傅里叶变换分析

按照傅里叶变换，对任意一个空间（或时间）域x中的函数f（x），在空间（或时间）频率域（频率v）存在一个对应的函数F（v），它们的关系是：

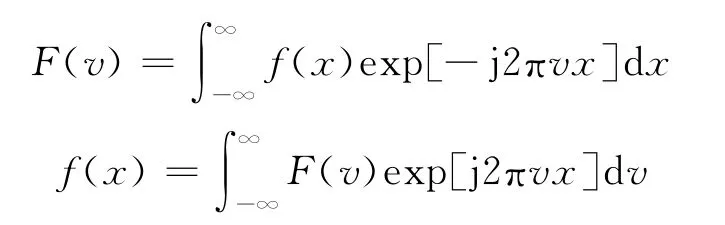
从f（x）给出F（v）称为傅里叶变换，从F（v）给出f（x）称为傅里叶逆变换。它们表示，一个物理量，可以在空间（或时间）域x用函数f（x）表示，也可以通过傅里叶变换在空间（或时间）频域v用函数F（v）表示。函数F（v）称为函数f（x）的频谱，它给出了构成函数f（x）的各个频率成分情况。

通过傅里叶变换，可以简单地从空间域转换到空间频域。因此，对成像过程从空间域转换到空间频域，只需要对空间域的成像进行傅里叶变换。即：

按照傅里叶变换卷积定理，则应有：

写出它们各自的具体表示式，并用各自的符号，则有：

这时则可写出：

这个关系式说明，对于线性平移不变系统，在空间频域，（输出）像的频谱可以用（输入）物的频谱与成像系统点扩散函数的频谱的乘积表示。像频谱与物频谱的关系则可写为：

式中H（v）称为成像系统的传递函数。

按照傅里叶变换公式，传递函数一般为一复数，可以写成模与幅角积的形式，即：

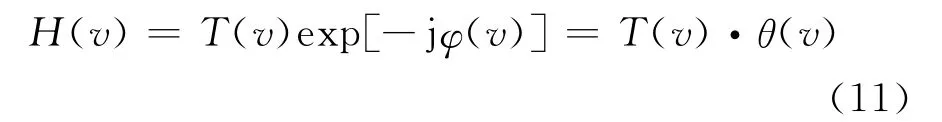
式中v为空间频率；T（v）为调制传递因子；θ（v）为相位传递因子。T（v）反映成像过程中调制度的变化，θ（v）反映成像过程中相位的变化，图8示意性地显示了调制度和相位在成像过程的变化。

3.3 调制传递函数MTF

调制传递因子T（v）表示的是像的调制度Mi和物的调制度M0的关系，即：

图8 成像过程调制度和相位的变化

即，T（v）给出了通过成像系统后，像的调制度与物的调制度的关系。T（v）与空间频率v的函数关系称为调制传递函数，简记为MTF。调制传递函数曲线的典型样式如图9。由于T（v）决定于成像系统点扩散函数的傅里叶变换，因此，调制传递函数也决定于成像系统的点扩散函数。

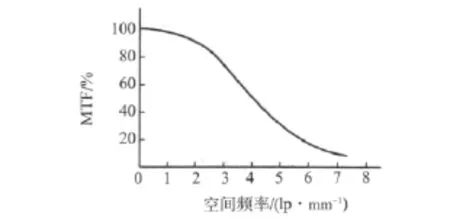
图9 调制传递函数曲线样式

调制传递函数具体给出了成像系统对不同空间频率细节成像后调制度改变的情况。细节尺寸越小，对应的空间频率越高，经成像系统成像后调制度降低越多。细小缺陷显然具有更高的空间频率，因此，成像后调制度降低将大于较大尺寸缺陷。也就是将更难成像。由于任何接收器存在可识别的调制度阈值，因此成像系统存在可识别的最高空间频率，也即可识别的细节最小尺寸。

从此不难理解，对任何检测技术，都存在可检验的缺陷最小尺寸。

4 线扩散函数、边扩散函数与不清晰度

4.1 线扩散函数与边扩散函数概念

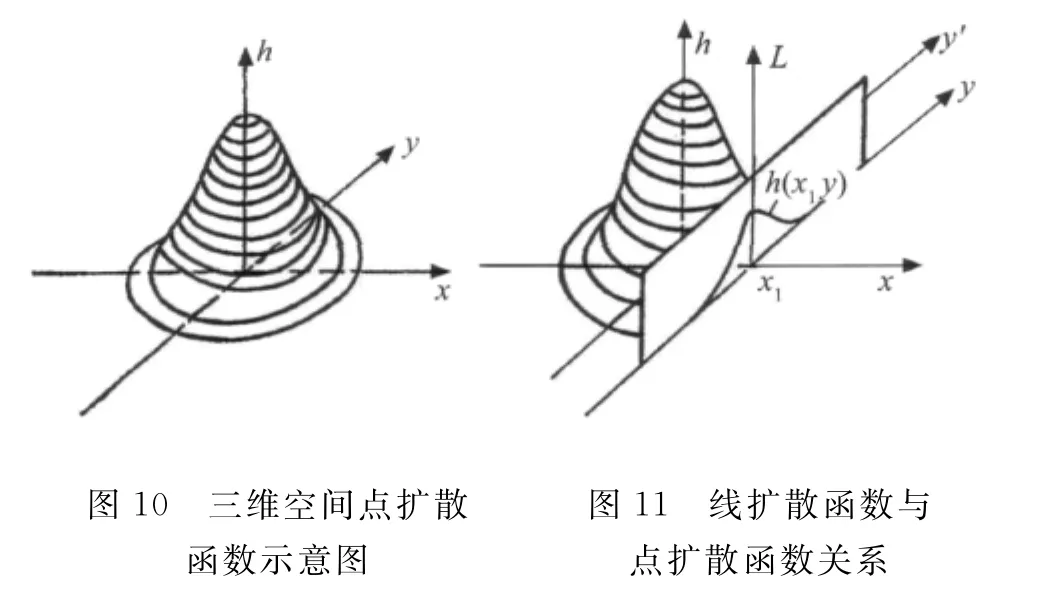
在前面的叙述中，一直采用一维空间，并仅使用点扩散函数概念。在实际三维空间中，点扩散函数应是二维函数，这时点扩散函数可记成h（x，y）。其图像如图10所示。对于线性平移不变系统，由于系统的平移不变性，点扩散函数可以写成一维形式。

在成像理论研究中，除了点扩散函数还引入了线扩散函数（LSF）。线扩散函数是成像系统对线物体所成的像，也就是对线物体的响应。容易理解，线扩散函数是点扩散函数在某方向的迭加，图11表示了这种情况。即：

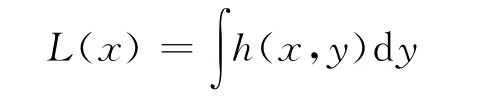
显然，它也应是一个二维函数。同样，对于线性平移不变系统，考虑到系统的平移不变性，对于系统的主要成像区，线扩散函数可以写成一维形式，一般将其记成L（x）。

在成像理论研究中，除了点扩散函数、线扩散函数（LSF），还引入了边扩散函数（ESF）。边扩散函数是成像系统对直边所成的像，也就是对直边物体的响应。对于线性平移不变系统，也可写为一维函数，记成E（x）。线扩散函数与边扩散函数两者的关系为：

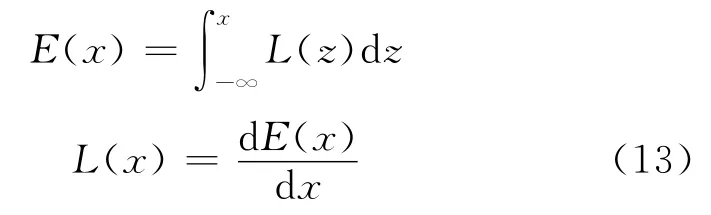
这样，边扩散函数与点扩散函数关系应为：

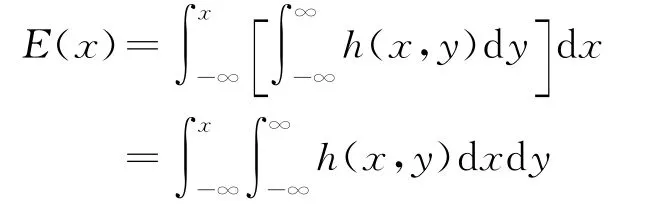
即，边扩散函数是线扩散函数曲线下的面积，而线扩散函数可从边扩散函数曲线的导数得到。图12画出了对应的线扩散函数和边扩散函数曲线。

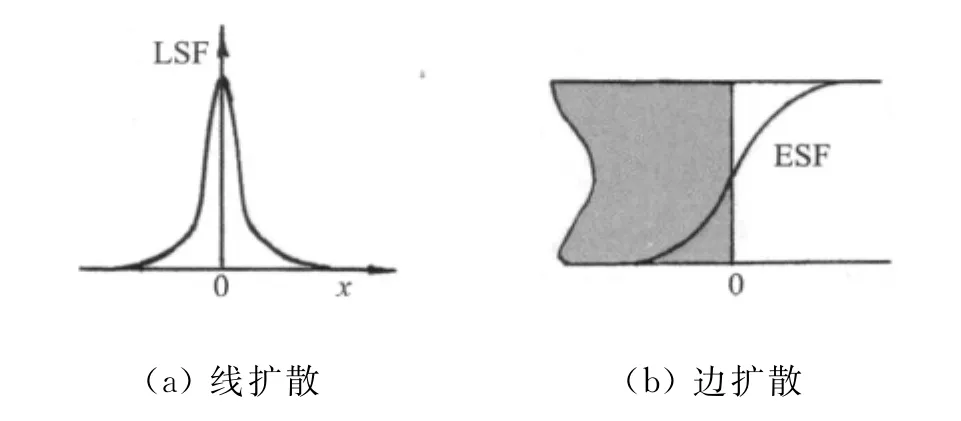
图12 成像系统的线扩散函数和边扩散函数

在三维空间中成像系统的传递函数，理论上一般采用线扩散函数的傅里叶变换。

4.2 线扩散函数与不清晰度关系

对于射线检测技术，经常使用的是简单的不清晰度概念U。按照不清晰度概念，它定义为射线检测技术中的不清晰度曲线的扩展宽度。不清晰度曲线实际就是边扩散函数曲线，因此，不清晰度实际也就是边扩散函数的扩展宽度。由于线扩散函数为边扩散函数的导数，不清晰度也是线扩散函数的扩展宽度。

在射线检测技术，对于实际测量不清晰度，不同研究人员采用了不同的方法。通常的建议是用直线给出的扩展宽度作为不清晰度，该直线下的面积与复杂形状不清晰度曲线下的面积应相等，图13（a）显示了具体情况，图中的直线BC就是所采用的直线。在近似处理问题时，用该直线扩展宽度作为不清晰度，也就是用一矩形函数近似线扩散函数，矩形函数宽度现在常用BW表示。图13（b）显示了它们之间的关系。

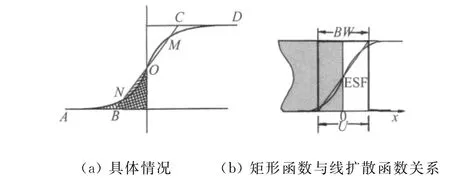
图13 射线检测技术的不清晰度测定

可见，无论不清晰度的理论概念和实际测量，都显示它是边扩散函数扩展宽度的转换概念。也就是，不清晰度是相关于射线检测技术作为成像系统的扩散函数的概念。因此，它成为影响射线检测技术成像系统调制传递函数的重要因素。当然，调制传递函数还将与不清晰度曲线的形状密切相关。也就是，不清晰度将直接影响射线检测技术系统对不同空间频率细节成像的质量。

5 瑞利判据

点扩散函数的扩散范围表征了成像系统的分辨能力。当点扩散函数扩散存在一定范围时，在得到的像上，某一点实际是物中一定范围内点贡献的迭加结果。点扩散函数扩散的范围越小，涉及的物中点的范围越小，成像系统的分辨能力越高。当两个物点逐渐靠近时，它们的像也将互相靠近，直至重叠不能分辨。

在光学理论上，瑞利把图中一个点物衍射图样的中央极大与近旁另一个点物衍射图样的第一极小重合，作为光学成像系统的分辨力极限，认为此时系统恰好可以分辨开两个点物。这称为瑞利判据，至今，一直采用该条件作为分辨力标准。

实际应用中的瑞利判据如图14所示。即，当二等强度孤立线像合成分布的中央最小值（图中F点）不高于两边最大值（图中G点）的0.81时认为可分辨。对当二等强度孤立点像合成分布的中央最小值（图中F点）不高于二边最大值（图中G点）的0.735时认为可分辨。

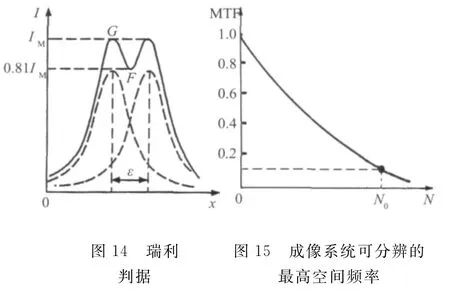
将瑞利判据转换到成像系统的调制传递函数曲线上，运用调制度概念可确定成像系统可分辨的最高空间频率。简单计算即可以得到，对于线状图像，决定最高空间频率的调制度近似为0.11。图15是其示意图，图中N0就是成像系统可分辨的最高空间频率。采用双丝像质计测定的不清晰度对应的空间频率，就是对应调制度近似为0.11处的空间频率。应注意的是，某些标准采用调制度为0.2处的空间频率作为成像系统可分辨的最高空间频率。

（未完待续）

［1］王之江，伍树东.成像光学［M］.北京：科学出版社，1991.

［2］母国光，战元龄.光学（第2版）［M］.北京：高等教育出版社，2009.

［3］加斯基尔J D，著.线性系统· 傅里叶变换·光学［M］.封开印，译.北京：人民教育出版社，1981.

［4］麦伟麟.光学传递函数及其数理基础［M］.北京：国防工业出版社，1979.

［5］谢敬辉，廖宁放，曹良才.傅里叶光学与现代光学基础［M］.北京：北京理工大学出版社，2007.

［6］廖延彪.成像光学导论［M］.北京：清华大学出版社，2008.

［7］Halmshaw R.Industrial Radiology： Theory and Practice［M］.New Jersey：Applied Science Publishers LTD ，1982.