基于摩擦模型的超声波电动机速度控制

李鸿征，王春霞

(焦作大学，河南焦作454003)

0引 言

超声波电动机是一种全新概念的新型驱动装置，是20世纪80年代中期发展起来的，它利用压电材料的逆压电效应，将电能转换为弹性体的超声振动，并将摩擦传动转换成运动体的回转或直线运动。由于超声波电动机具有转速低、转矩大、结构紧凑、体积小、噪声小等一系列优点，特别是它与传统电磁式电动机相比具有无磁并且不受磁场影响的特点，因此更适合工业控制、精密仪器仪表、车载电器、办公自动化设备和航天器制造等领域的配套使用。

伴随着超声波电动机日益广泛地应用于工业控制、精密仪器仪表、车载电器、办公自动化设备和航天器制造等领域，如何有效地控制超声波电动机成为一个迫切需要解决的问题。因为超声波电动机的运动特性受到振动频率、温度和负载的影响而表现出很强的非线性特征和时变特性，难以建立一个通用的数学模型来精确描述其动、静态特性，因而很多依赖模型的方法受到了限制。于是对超声波电动机的控制多采用基于简化模型的自适应控制或结合其他智能辨识/控制的工具，如:神经网络、模糊推理等方法来实现。

许多研究者在超声波电动机的控制问题上做出了努力。Tomonobu Senjyu等人使用神经网络补偿超声波电动机，达到了转速控制的目的;Jürgen Maas等人利用神经网络补偿电动机的非线性特性，使电动机的控制性能得到提高;Faa-Jeng Lin使用模糊自适应方法跟踪电动机的时变特性黄青华、魏守水等使用的模糊神经网络控制USM的频率算法，都可以实现位置控制;李华峰等人分别使用自适应控制与比例控制结合的方法控制了电动机的位置，和使用模糊控制调节相位差，补偿电动机运行的非线性、时变和死区;贺红林等人利用模糊、自校正技术相结合的方法建立控制系统。

另外，Senju T为了提高控制系统的性能，使用模糊神经网络来对超声电动机的死区非线性进行辨识和补偿，然后结合自适应控制和PI控制方案对电动机进行了位置控制。

Bigdeli N使用Hammerstein模型来描述超声波电动机的运动特性，并据此设计了基于模型的预测控制器，仿真结果表明，此控制方案可以改善超声波电动机控制性能。但是这种方案使用静态非线性模块来描述超声波电动机因外界条件如负载、温度的改变而产生的非线性的影响，模型过于简单，很难直接应用到实际的超声波电动机的控制中。

Lin F J利用神经网络设计了超声波电动机在线辨识和在线控制方案，通过改进BP神经网络的输入层激励函数和学习率，保证了网络的稳定、快速收敛，实验取得了满意的控制效果。

1基于LuGre摩擦模型的超声波电动机控制

在系统控制中常用控制规律有PD、PI和PID，但是由于PID控制具有较完善的功能，并且具有简单的控制结构而又比较容易整定，因此被广泛的应用于工业过程控制中。PID控制系统的基本原理框图如图1所示，主要由PID控制器和被控对象组成。

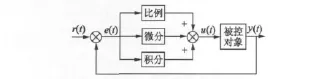
图1 模拟PID控制系统原理框图

由图1可知，PID控制器是按照系统偏差，即给定值r(t)与实际值y(t)之间的偏差进行P、I、D运算的一种线性控制器，其偏差、控制规律和传递函数的形式:

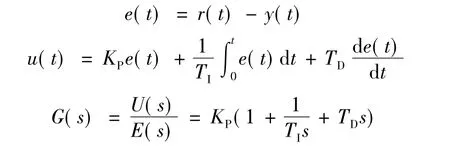
式中:KP为比例系数;TI为积分时间常数;TD为微分时间常数。

比例环节KP能够对系统产生的偏差进行及时调节，但是不能最终消除偏差，因为一旦没有偏差，则控制作用将不复存在;积分环节用于消除系统的稳态误差，从而提高系统的控制精度。积分时间常数TI反映了积分作用的大小，TI大则积分作用强;微分环节TDs能够对系统偏差信号产生超前控制，可以减小或避免系统调节过度，从而减小系统超调量，加快调节速度，缩短调节时间。

采用PID控制是系统控制中的一种优越的控制方法，但是由于PID控制器的控制参数较多，需要对比例系数KP、积分时间常数TI和微分时间常数TD同时进行设计和调节才能获得最佳控制效果，因此通常采用经验设计公式，常用的齐格勒-尼柯尔斯调节律，即Z-N法，它有两种方法。

第一种方法:要获得控制对象单位阶跃响应曲线，可以进行实验或采用动态仿真。在控制对象中没有积分器和主导共轭复数极点的情况下，响应曲线是如图2所示的S型(但是如果曲线不为S型，则不能应用此方法)。可以用延迟时间L和时间常数T来描述S型曲线。

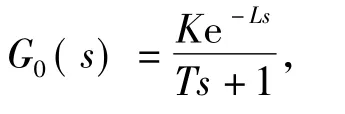
图2 S型曲线

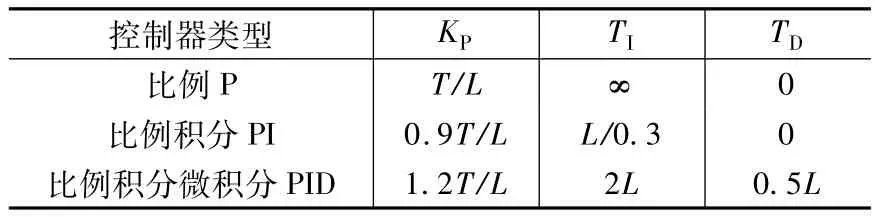
表1 齐格勒-尼柯尔斯调整法则(方法一)

齐格勒-尼柯尔斯法则的经验公式如下:

第二种方法:设TI=∞和TD=0，在只有比例控制作用时，调节KP，使之从零增加到系统的输出首次呈现持续振荡，则此时的增益值KP=KC，称为临界值。但是，当不论怎样调节KP的值都不会使系统的输出出现持续振荡时，则不能使用此种方法。

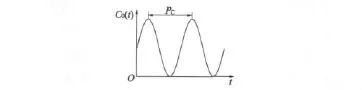
图3 实验法

可以通过实验的方法确定临界增益KC和相应的周期PC，如图3所示。比例系数KP、积分时间常数TI和微分时间常数TD的值可以根据表2的齐格勒-尼柯尔斯调整法则确定。齐格勒-尼柯尔斯调整法则第二种方法调整的PID控制器的数学模型:

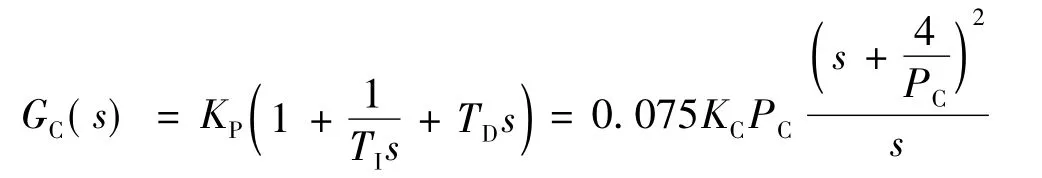
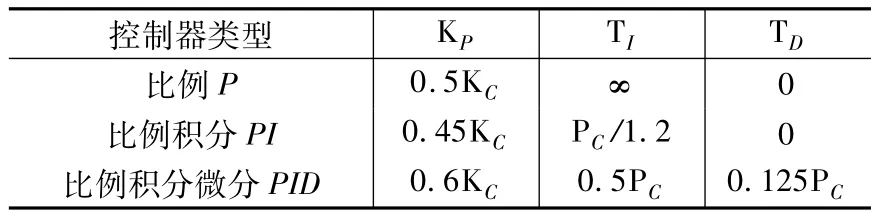
表2 齐格勒-尼柯尔斯调整法则(方法二)

本文采用齐格勒-尼柯尔斯第二种方法进行调节PID各参数。因为PID控制规律仅适用于线性反馈控制系统，对于包含摩擦这种非线性、非光滑的系统，使用PID控制会引起极限环或者不稳定的现象出现。因此在对超声波电动机使用PID控制方案时首先要对系统的摩擦环节进行补偿，然后再结合PID控制器进行控制，这样一个整体超声波电动机模型控制方案即可被建立起来。

2基于模型补偿控制的超声波电动机仿真

为了检验超声波电动机模型控制方案的效果，为此进行仿真实验。首先对超声波电动机进行摩擦补偿，然后结合PID控制器建立起来整体控制方案，如图4所示。仿真实验将证明摩擦补偿后的超声波电动机PID控制方案的可行性。为了进一步验证控制方法在噪声存在下的有效性，在电动机的输出转速中加入3%的扰动信号。

图4 超声波电动机摩擦补偿的PID控制整体框图

为了说明基于模型补偿的控制效果的优势，使用逆模补偿PID控制与无补偿PID控制得到的结果来进行比较。

图5为有摩擦补偿的超声波电动机PID控制效果图和误差曲线，图6为无摩擦补偿的PID控制效果图和误差曲线。图5(a)和图6(a)中的实线表示实际输出，虚线表示仿真输出。

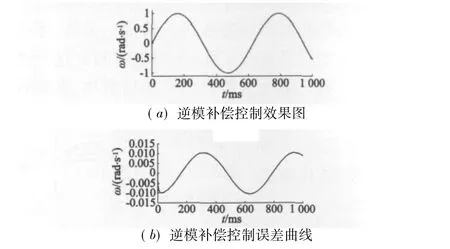
图5 摩擦补偿控制效果及误差曲线图

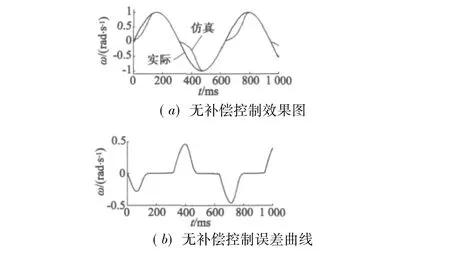
图6 无摩擦补偿控制效果及误差曲线图

从图6(b)的无摩擦补偿时的误差曲线得到，电机输出转速误差的方均根值为23．9%;而从图5(b)所示进行摩擦补偿后的误差曲线，得到电机输出转速误差的方均根值为0．66%。

将图5和图6进行对比可以看到，无摩擦补偿的PID控制器在整个控制过程中虽然完全跟踪了转速趋势，但是跟踪曲线和误差曲线都表现出了严重的死区特性。然而电动机工作性能要求快速、准确和精确，因此为了提高超声波电动机的整体性能，就需要克服摩擦补偿死区现象。实现补偿摩擦后可以使系统在起动阶段满足对快速敏感性的要求，并且兼顾了与平缓区的稳定性、准确性等性能要求。这是采用LuGre摩擦模型补偿后的一大优点。

为了检验系统模型的控制效果，对输入模型参数进行仿真，静态参数:库仑摩擦力FS=1．41 V，最大静摩擦力 FS=1．83 V，Stibeck 速度 vS=0．26 mm/s;动态参数:角度刚度系数σ0=22 V·s/mm，滑动阻尼系数σ1=0．17 V·s/mm。图7为电机转速输出曲线，虚线部分为实际输出。

图7 模型仿真效果图

结果表明，采用LuGre摩擦模型补偿，可以更加真实地反映实际系统的控制效果。

3结 语

根据超声波电动机目前的控制现状，结合PID控制器，实现了基于LuGre摩擦模型的超声波电动机模型控制，并且使用Z-N法得到了控制器的三个控制参数。仿真实验验证与实际系统对比可知，对超声波电动机摩擦补偿后使用PID控制算法具有可行性和有效性。

［1］ 周金柱，段宝岩，黄进．LuGre摩擦模型对伺服系统的影响与补偿［J］．控制理论与应用，2008，25(6):8-12．

［2］ 程昱，钟宜生，许文立．采用自校正模糊PI控制的超声波电机速度控制［J］．微特电机，2002，30(4):30-33．

［3］ 金龙，禇国伟，胡敏强，等．超声波电机速度与定位控制系统［J］．中国电机工程学报，2005，25(1):134-139．

［4］ 史婷娜，徐绍辉，夏长亮，等．超声波电机模糊-PI双模自适应速度控制［J］．电工技术学报，2003，18(3):2-5．

［5］ 于志伟，曾鸣，乔大鹏．采用复合控制的直流力矩电机摩擦补偿［J］．电机与控制学报，2008，12(5):57-62．

［6］ 吴盛林，刘春芳．基于LuGre模型的电液伺服系统摩擦力矩动态补偿［J］．机床与液压，2003(2):68-70．