高速永磁同步电动机无速度传感器矢量控制
王继强,李国华,佟宁泽
(1.辽宁工程技术大学,辽宁葫芦岛125105;2.冶金自动化研究设计院伺服系统研究设计所,北京100071)
0 引 言
为了实现对转矩的高品质控制,获得优良的动态性能,永磁同步电动机(以下简称PMSM)一般需要安装高精度、高分辨率机械式速度和位置传感器[1-3]。高速永磁同步电动机转子转速高达30 000~100 000r/min。为了保证高速运行的安全,其转子长度必须受到严格的控制。安装机械式传感器,必将增加转子长度,从而影响高速永磁同步电动机转子的动力学性能。同时,高速永磁同步电动机的定子电源频率高达1 000 Hz左右,其高次电磁谐波和高频振动对机械传感器精度造成较大影响[4-5]。无速度传感器不但能准确估计转子速度和转子位移,而且能避免机械式传感器对高速电机转子动力学性能的影响。因此无速度传感器对高速和超高速电机而言具有重要的意义。
目前,无传感器PMSM矢量控制中转子位置和速度的估计方法有多种。文献[1]采用一种基于MRAS的永磁同步电机速度辨识方案并对转速和定子电阻进行辨识。文献[6-10]分别采用扩展的卡尔曼滤波、神经网络、滑模变结构等方法建立了永磁同步电动机无速度传感器模型,但这些算法的设计比较复杂,实现起来对硬件的性能要求较高。文献[11]提出了一种基于电磁转矩反馈补偿的新型PI速度控制器,提高了速度环的抗负载转矩扰动能力。文献[12-13]对高性能变频调速控制系统中存在典型离散控制问题进行了深入的分析。文献[14]分析了电机参数误差对永磁同步电机性能的影响。文献[15-20]分别利用模型参考自适应、小波变换和神经网络、HHT、Park模型等方法计算了永磁电机的参数,但这些方法较复杂。文献[21-22]利用场路耦合方法进行了异步电机和同步电机参数计算。
本文首先利用场路耦合方法计算了高速永磁同步电动机的交、直轴电感、转子磁链等参数,并建立了一种以定子电流为状态变量的高速永磁同步电动机无速度传感器模型。该速度传感器将参考模型q轴电流与可调模型q轴电流之差作为误差信号送入PI调节器调节后得到估计转速。该模型结构输入变量少,结构相对简单,可靠性高,特别对电动机的高速运行具有有效性和可行性。
1 隐极永磁同步的速度估计模型
在同步dq坐标系中,隐极PMSM的电压方程[2]:

令:

若以估计数表示:
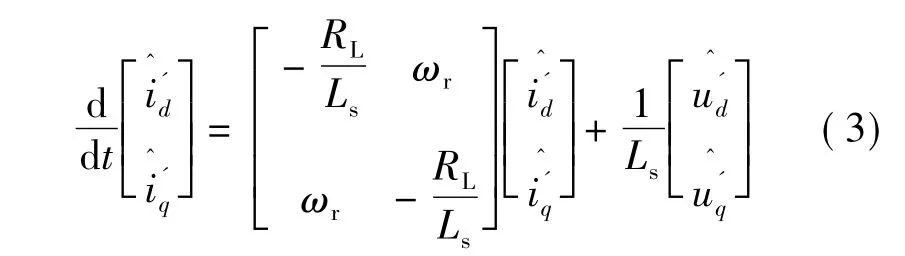
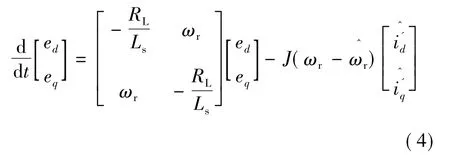
即:

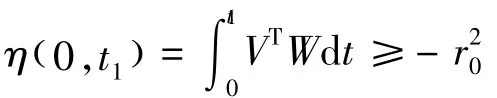

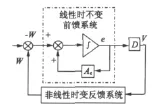
图1 等效非线性反馈系统
式中:r0为一有限正数。
将V和W分别代入:

对Popov积分不等式进行逆向求解,就可得到转速估计:
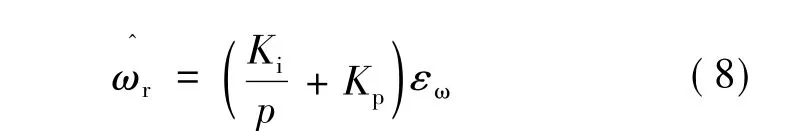

图2 MARS估计转子速度和位置
2 高速永磁同步电动机的参数计算
高速永磁同步电动机的额定转速为60 000 r/min,为了防止永磁体在巨大的离心力作用下破坏,采用非导磁高强度合金钢护套对永磁体进行保护[5],如图3 所示。为准确计算该电机的交、直轴电感、永磁体磁链等参数,利用场路耦合方法建立了其有限元模型,并利用该模型计算了永磁体磁链。高速永磁同步电动机的转子磁链可以由下式计算:


图3 转子结构示意图
高速永磁同步电动机在60 000 r/min时的空载电压E0如图4所示。由式(9)可得其转子磁链约为 0.074 Wb。

图4 空载时电枢绕组上的反电动势
对于直轴电感,先求出空载时的气隙基波磁通Φ10,再求出直轴电流等于 Id时的气隙基波磁通Φ1N,便可利用式(10)计算直轴电感[20]:
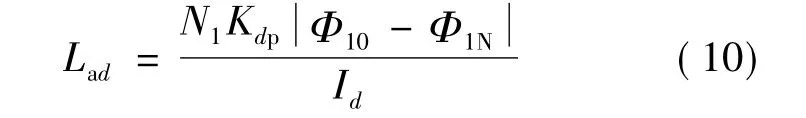
对于交轴电感Laq,直接在定子绕组中通入交轴电流Iq,求出此时产生的气隙磁通Φaq,于是:

高速永磁同步电动机某时刻空载和负载气隙磁密沿空间的分布如图5所示。由图5可知,负载时气隙磁密存在较大的畸变,经傅里叶分析可以得到气隙磁密的基波幅值为0.16 T,如图6所示。应用式(10)可得其直轴电感为0.11 mH。由于该电机为隐极结构,交轴电感也为0.11 mH。
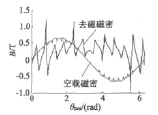
图5 空载和去磁时的气隙磁密分析
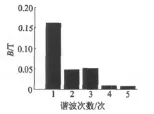
图6 气隙磁场的空间谐波分析
3 仿真结果及分析
本文利用MATLAB/Simulink仿真来检验高速永磁同步电动机无速度传感器辨识算法的正确性。给定电机转速为60 000r/min,给定转矩为12 N·m,其额定功率为75 kW,其转子转动惯量为0.025 kg·m2。给定和实际的速度上升曲线如图7所示,给定和实际的转矩如图8所示。电机在5.5 s后速度稳定在60 000r/min。电机速度上升到额定转速之前,其输出转矩为最大输出转矩,约为30 N·m,约为额定转矩的2.5倍。当转速上升到额定转速后,其给定转矩为零。6 s时,给电机施加额定负载转矩12 N·m。
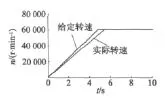
图7 高速永磁同步电动机的给定和实际速度上升曲线

图8 高速永磁同步电动机的给定和实际转矩
高速电机的相电流如图9所示,额定负载转矩时电流幅值约为120 A,有效值约为85 A。相电流分解为直轴电流和交轴电流,如图10和图11所示。

图9 高速永磁同步电动机的相电流
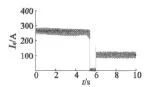
图10 高速永磁同步电动机的q轴电流

图11 高速永磁同步电动机的d轴电流
高速永磁同步电动机的交轴电流与负载转矩成正比,空载时约为零,额定负载时其平均为108 A。而直轴电流幅值在-40~40 A之间变化,平均值约为零,高速永磁同步电动机的电磁转矩可由式(12)计算,其电磁转矩为12 N·m。

4 结 语
高速永磁同步电动机的转子结构和传统的永磁电机转子结构有所不同,为了准确计算该电机参数,建立了其场路耦合模型并计算了参数计算。在参数计算的基础上,建立了以定子电流为参考变量的高速永磁同步电动机自适应速度估计模型,并进行了仿真分析,验证了参数计算和速度估计模型的正确性。
[1] 齐放,邓智泉,仇志坚,等.基于MRAS的永磁同步电机无速度传感器[J].中国电机工程学报,2007,22(4):53 -58.
[2] 王成元,夏加宽,孙宜标.现代电机控制技术[M].北京:机械工业出版社,2009:179-207.
[3] Leidhold R,Mutschler P.Speed sensorless control of a long-stator linear synchronous motor arranged in multiple segments[J].IEEE Transactions on Industrial Electronics,2007,54(6):3246 -3254.
[4] 王继强,王凤翔,宗鸣.高速电机磁力轴承-转子系统临界转速的计算[J].中国电机工程学报,2007,27(27):94 -98.
[5] 王继强,王凤翔,孔晓光.高速永磁发电机的设计与电磁性能分析[J].中国电机工程学报,2008,28(20):105 -110.
[6] 陆华才,徐月同.基于AEKF的永磁直线同步电机速度和位置估计算法[J].中国电机工程学报,2009,29(33):91-94.
[7] 刘侃,章兢.基于自适应线性元件神经网络的表面式永磁同步电机参数在线辨识[J].中国电机工程学报,2010,30(30):68-73.
[8] 贾洪平,孙丹,贺益康.基于滑模变结构的永磁同步电机直接转矩控制[J].中国电机工程学报,2006,26(20):134-138.
[9] Chu Jianbo,Hu Yuwen,Huang Wenxin,et al.Animproved sliding mode observer for position sensorless vector control drive of PMSM[C]//Power Electronics and Motion Control Conference.2009,6:1898-1902.
[10] 王庆龙,张崇巍,张兴.基于变结构模型参考自适应系统的永磁同步电机转速辨识[J].中国电机工程学报,2008,28(9):71-75.
[11] 郭新华,温旭辉,赵峰,等.基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器[J].中国电机工程学报,2010,30(27):7-13.
[12] 张剑,温旭辉,刘均,等.一种基于DSP的PMSM 转子位置及速度估计新方法[J].中国电机工程学报,2006,26(12):145-148.
[13] 胡斯登,赵争鸣,袁立强,等.高性能变频调速系统的离散控制问题研究[J].中国电机工程学报,2010,30(30):1 -6.
[14] 陈阳生,黄碧霞,诸自强,等.电机参数误差对永磁同步电机弱磁性能的影响[J].中国电机工程学报,2008,28(6):92-97.
[15] 徐占国,邵诚,冯冬菊.基于模型参考自适应的感应电机励磁互感在线辨识新方法[J].中国电机工程学报,2010(3):71-76.
[16] 王亮,王公宝,马伟明,等.基于小波变换和神经网络的同步电机参数辨识新方法[J].中国电机工程学报,2007,27(3):1-6.
[17] 李天云,高磊,聂永辉,等.基于HHT的同步电机参数辨识[J].中国电机工程学报,2006,26(8):153-158.
[18] 孙黎霞,鞠平,高运华,等.基于Park模型的同步发电机参数辨识[J].中国电机工程学报,2009,29(19):50-56.
[19] 王飞.永磁同步电机无传感器矢量控制方法研究及仿真[D].上海:上海交通大学,2008.
[20] 常凯.基于模型参考自适应的永磁同步电机无速度传感控制系统的设计[D].沈阳:东北大学,2009.
[21] 陶果,邱阿瑞,柴建云,等.永磁同步伺服电动机的磁场分析与参数计算[J].清华大学学报(自然科学版),2004,44(10):1317-1320.
[22] 张飞,唐任远,陈丽香,等.永磁同步电动机电抗参数研究[J].电工技术学报,2006,21(11):7-10.

