基于RBF控制的开关磁阻电动机直接转矩控制

刘春元，王勉华，王宗刚

(1.河西学院，甘肃张掖734000;2.西安科技大学，陕西西安710054)

0 引 言

开关磁阻电动机(以下简称SRM)是继异步电动机之后的又一种新型电机，具有结构简单、起动转矩大、控制参数灵活、调速性能优越等优点;但是SRM是双凸极结构，通常工作在磁饱和状态，导致了SRM的电磁特性呈高度非线性，难以用一个精确的数学表达式来描述SRM的电磁关系［1－2］。目前，对SRM主要的研究方向集中为两点，即电机本体的设计以及控制方法的研究。本文主要从控制方面展开论述。

常规PID控制器由于结构简单、实现容易、控制方便等优点，仍处于主导地位，得到了广泛应用，其核心就是参数的整定。但随着控制对象系统的越来越复杂，常规PID控制器的参数是固定不变的，在非线性系统中很难达到良好的控制效果。由于SRM的电磁关系呈现为严重的非线性，所以常规的控制方法很难达到控制的预期效果。近年来，随着人工神经网络和控制理论(特别是智能控制理论)的逐渐发展，由人工神经网络构成的自适应控制器逐渐在非线性系统中得到了广泛的应用，解决了非线性和不确定系统的控制方面难题。国内外专家学者将神经网络控制器应用于开关磁阻电动机调速系统(以下简称SRD)中，取得了很好效果。文献［3］提出了单神经元PID控制器;文献［4］是以BP神经网络整定的PID控制器;文献［5］提出了模糊PID控制器等智能控制器，以实现对复杂系统的控制。基于此，本文提出了一种基于RBF神经网络自整定的PID控制器，利用直接转矩控制的思想，针对SRM严重的非线性，利用神经网络构成SRM的控制器。为了进行对比，本文同时也研究了常规PI的控制方法，结果表明，本文的方法与单一常规PI控制器相比，具有控制精度高、响应时间短、超调较小的优点，并且当系统中存在干扰时，具有很好的自适应性能力以及很好的鲁棒性。

1 SRM数学模型

(1)电压方程

根据电磁感应定理和能量损耗定理，施加在定子各相绕组两端的电压，等于定子因磁链变化而产生的感应电势和电阻压降之和，即:

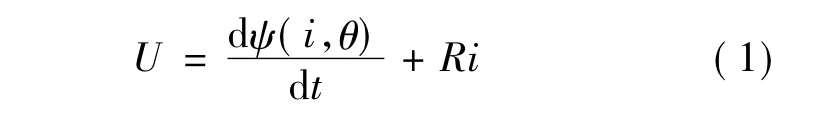
式中:U、R、i依次是电机定子相电压、相电阻和相电流;θ为电机转子与定子的相对位置角;ψ(i，θ)为电机定子的相绕组磁链。

(2)磁链方程

对于SRM，两相之间的自感相对互感要大得多，通常可以将互感忽略不计。这样一来就可以用下式来描述SRM每相绕组磁链ψ(i，θ):

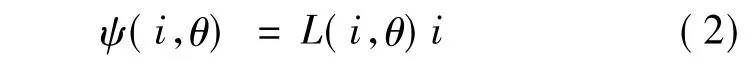
式中，相电感的值是由相电流i和转子位置角θ确定，且它们之间为非线性函数，故很难用解析的方法就得式(1)的解析值，目前主要的方法是通过有限元、神经网络拟合等方法进行计算。

(3)转矩方程

在一个控制周期中，电机的电流基本上不发生变化。由SRM的瞬时转矩理论可知，转矩可以用机械能跟转子位置角的导数求取，即可以用下式表达:

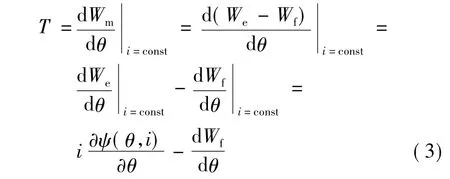
式中:Wm为机械能;We为磁共能;Wf为磁场储能。

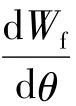
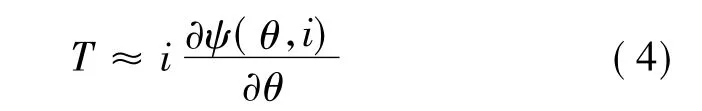
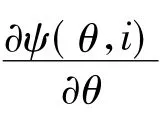
(4)运动方程

按照力学定律可列出SRM的转子机械运动方程:

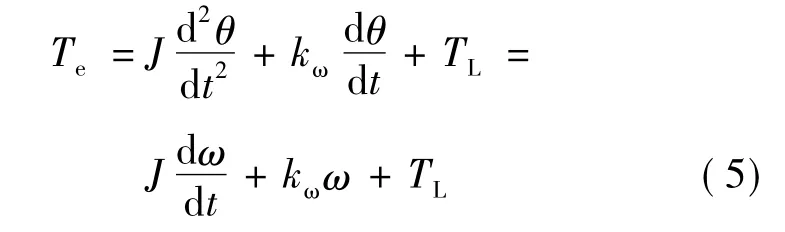
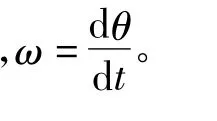
2 开关磁阻电动机调速系统(SRD)

SRD由控制器、功率变换器、位置检测、电流检测和SRM电机本体构成［6］，其结构图如图1所示。

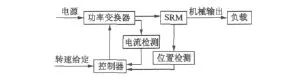
图1 SRD结构框图

在本文中，利用直接转矩控制构成SRD系统，其结构图如图2所示。内环包括磁链估算和转矩估算。磁链估算通过式(1)的变形即 φ=∫(U－iRs)dt得到，然后跟给定磁链比较，得到磁链差;转矩估算由SRM的输出模块给定;外环由具有自适应功能的RBF神经网络控制器，输入为给定速度与实际速度输出之差，经过RBF神经网络控制器，得到输出转矩T*，其值跟SRM模块的输出转矩T比较，得到转矩差值ΔT。送入开关表的信号为转矩差ΔT、磁链差Δψ以及区间判断信号Zone，利用直接转矩控制原理，控制功率变换器中的开关信号，以达到对磁链的控制，进而实现对转矩的精确控制。本文中，功率变换器选用不对称半桥型结构形式。

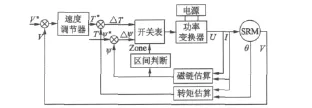
图2 SRM直接转矩控制结构图

3 RBF神经网络

近年来，RBF神经网络在非线性系统的建模、预测、分析等方面得到了广泛的研究和应用［7］。它是一种典型的由输入层、隐含层、输出层组成的三层前馈式神经网络，结构图如图3所示。

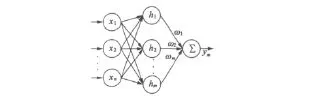
图3 RBF神经网络结构图

输入层为 X=［x1，x2，…，xn］，本文中，输入为转矩以及给定转速与实际转速的差值，隐含层为H=［h1，h2，…，hj，…，hm］T，节点选取为高斯函数，由线性神经元组成。输出为所有隐含层节点的输出之和。

对于单个网络输出的RBF网络，第k个隐含层单元的输出:

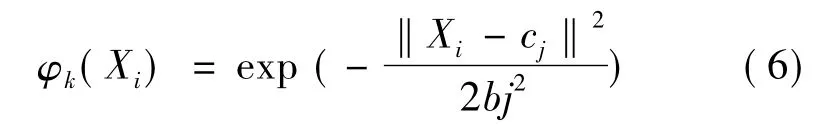
式中:‖ ‖表示欧式范数;Xi为第i个输入向量;cj为第j个隐含层节点的中心;bj为第j个隐含层节点的宽度。

整个网络的输出方程:

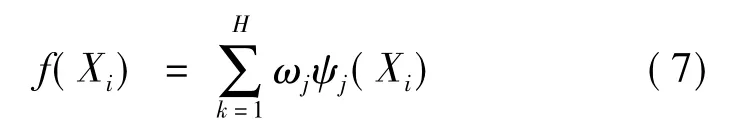
式中:ωj为第j个隐含层节点与输出层节点的连接权值;H为总的隐含层节点数。

定义辨识网络的性能指标Jm:

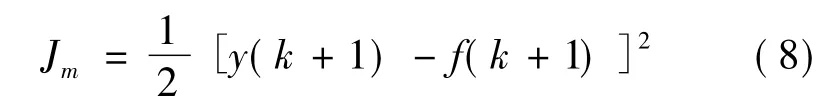
式中:f(k+1)为系统的实际输出;y(k+1)为系统的期望输出。本文中，cj、bj、ωj参数的确定，按照梯度下降法进行计算，即有下式确定:

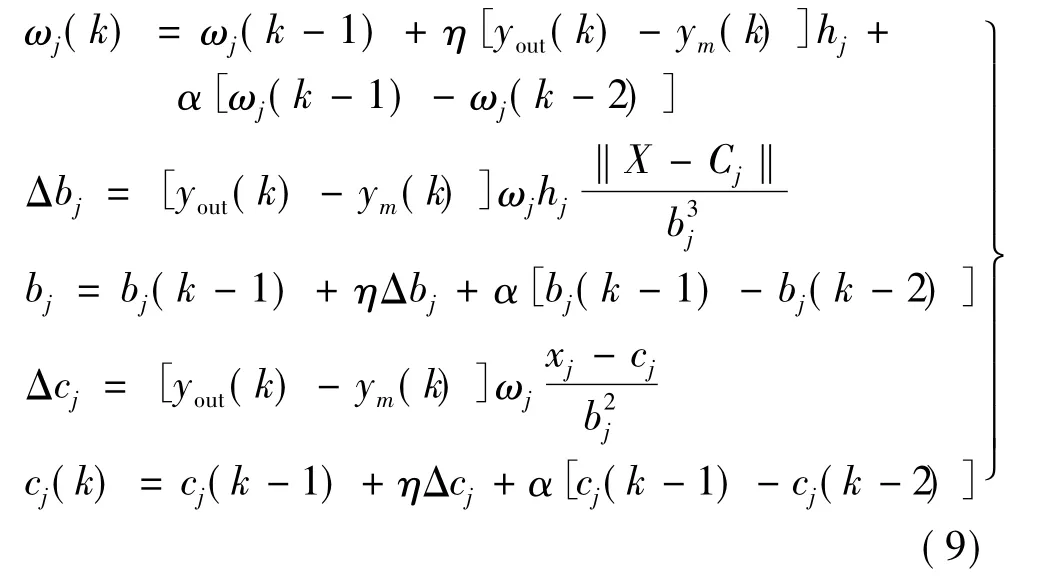
式中:α为动量因子;η为学习速率。

4 RBF速度调节器设计

针对SRM电磁严重的非线性，采用结构简单的常规PID调节器很难实现对其的精确控制。利用具有自适应的神经网络控制器，可以根据参数的变化，调节器发生相应的变化，根据神经网络能任意逼近任何非线性函数的特点，本文提出了基于RBF神经网络整定的PID控制。仿真实现图如图4所示。其中输入为给定速度n*与输出转速n之差Δn以及输出转矩Te，输出为参考转矩T*和PID参数。T*通过与Te比较，输入滞环调节器对转矩进行调节。

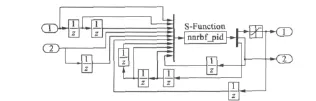
图4 RBF控制器的仿真实现

nnrbf_pid由S－function实现，主要功能是通过梯度下降法对 cj、bj、ωj参数的调整，完成基于 RBF网的PID调节器。为了使控制器更接近实用，在输出环节之后增加一个限幅环节。

5 仿真结果及分析

本文在MATLAB中建立了SRM的直接转矩控制，控制器采用上述的RBF自适应控制。调速系统的仿真模型，如图5所示。

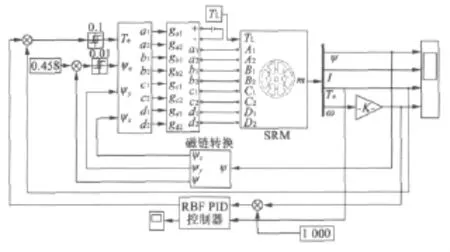
图5 整体仿真图

本文中，以60 kW、四相8/6结构的SRM为研究对象，给定转速n=1 000 r/min。开始时，系统运行在空载状态，即TL=0，同时为了验证该系统的抗干扰能力，当系统运行0.4 s后，使系统由空载转换为带TL=12 N·m的负载，于0.75 s时再变为空载，在此过程中，要求电机的速度n要稳定在给定转速1 000 r/min。为了与PI控制器进行比较，仿真时控制器分别采用了PI控制与RBF两种控制方法，局部速度响应曲线如图6所示。

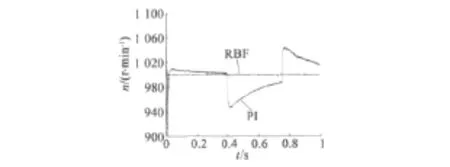
图6 局部速度响应曲线

从图6中可以看出，仅仅利用PI控制器，系统的超调比较大，约为4%，且上升时间比较长;当系统中存在干扰时，到达到所要求的速度，调节时间比较长;而用RBF神经网络控制器，系统的超调明显减小，当存在干扰时，系统的自适应能力比较强，速度能一直维持在给定速度，抗干扰能力好。控制效果明显优于单一的PI控制器。

图7给出了系统的输出转矩曲线。可以看出，系统的起动转矩比较大，在限定值附近。系统稳定运行时，转矩脉动仅为±1 N·m，当加入干扰时，转矩能够很快地稳定在给定的值附近，充分证明了利用此种方法能有效地减少系统的转矩脉动。

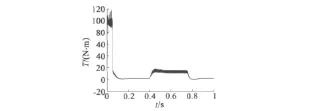
图7 转矩曲线

为了验证本文所阐述的直接转矩控制对SRM的控制效果，图8同时给出了直接转矩控制与电流斩波控制的磁链轨迹图。从图中可以看出，前者幅值被限定在滞环宽度内，磁链轨迹是一个圆形，磁链幅值基本恒定，达到了直接转矩控制的目的;后者磁链轨迹接近四边形，达不到磁链幅值恒定的原则。从而证明了此种方法的控制效果要远远好于电流斩波控制的方法。

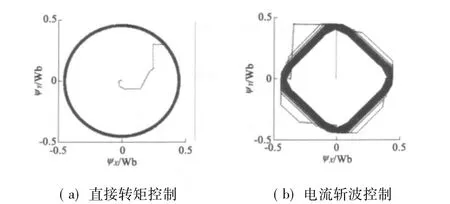
图8 磁链轨迹

6 结 语

本文充分利用RBF神经网络泛化能力强和计算速度快的优点，将直接控制控制技术与智能控制很好的结合起来，构成SRD控制器。仿真结果表明，该种控制方法具有较好的稳定性和动态响应能力;具有响应时间短、超调小的优点;系统动、静态性能良好，并且保证了系统的抗干扰能力，对系统具有较高的控制精度，对具体的工程实践有很好的指导意义。

［1］ 王宏华.开关磁阻电动机调速控制技术［M］.北京:机械工业出版社，1995.

［2］ 吴建华.开关磁阻电机设计与应用［M］.北京:机械工业出版社，2000.

［3］ 于力，欧阳红林.一种基于单神经元PID控制的多相永磁同步电动机矢量控制系统［J］.微电机，2007，40(8):89 －92.

［4］ 廖芳芳，肖建.基于BP神经网络PID参数自整定的研究［J］.系统仿真学报，2005，17(7):1711 －1713.

［5］ 李丽娜，柳洪义.模糊PID复合控制算法改进及应用［J］.东北大学学报(自然科学版)，2009，30(2):274 －278.

［6］ 王勉华，梁媛媛.开关磁阻电机直接转矩模糊PI控制器的设计［J］.电气传动，2010，40(1):51 ～54.

［7］ 黄友锐，曲立国.PID控制器参数整定与实现［M］.北京:科学出版社，2010.