基于粗糙熵模糊决策的河道采砂交易模式选择研究——以鄂赣边界可采区为例

杨高升,徐 新,梁钰翎,章晓锦

(河海大学 工程管理研究所,江苏 南京 211100)

基于粗糙熵模糊决策的河道采砂交易模式选择研究
——以鄂赣边界可采区为例

杨高升,徐 新,梁钰翎,章晓锦

(河海大学 工程管理研究所,江苏 南京 211100)

在分析我国河道采砂交易模式的政策背景和交易现状的基础上,运用粗糙熵模糊决策方法,建立针对直接许可、招标和拍卖三种交易模式的优选模型,对鄂赣边界可采区采砂交易模式进行选择。结果表明:该河段最佳交易模式为招标。由此得出结论:粗糙熵模糊决策法遵循河道采砂交易基本原则,对采砂交易模式的选择可行且有效。

河道采砂;交易模式;粗糙熵;模糊决策;公共资源

0 引 言

河道砂石资源既可以用于吹填固基、整治河道和疏浚港航等公益性项目,也可作为建筑市场上的优质廉价骨料。随着国民经济的快速发展,市场对砂石的需求量急剧增加,价格逐渐攀升,以南京市为例,黄砂中砂价格由2006年的3月的36.18元上升至2011年3月的71.09元。在可观利益的驱使下,违法滥采的混乱采砂局面给河势稳定、防洪安全、通航安全、水生态环境以及经济社会的发展带来严重的影响。为了维护河流的健康,保证其基本功能的正常发挥,必须从促进经济社会可持续发展的高度,对河道采砂进行规范的管理[1]。

为了从源头上保证河道采砂管理机制的有效性,必须对河道采砂的交易模式进行合理选择。当前的河道采砂交易研究主要停留在具体河段的交易模式介绍和交易管理优化上,较少涉及具体的交易模式决策模型设计,交易模式的选择主观性较强。本文正是针对上述问题,结合采砂活动的特殊性,探求合理的采砂交易模式决策模型,为具体河段的采砂交易提供指导。

1 河道采砂交易模式现状

1.1 交易模式政策法规

河道采砂交易机制体现在采砂交易模式的实施过程中,《长江河道采砂管理条例》第九条规定,国家对长江采砂实行采砂许可制度。《中华人民共和国行政许可法》第五十三条规定,行政机关应当通过招标、拍卖等公平竞争的方式做出决定。但是,法律、行政法规另有规定的,依照其规定。因此,河道采砂行政许可可以通过招标、拍卖及其他方式进行,并且遵循《中华人民共和国拍卖法》和《中华人民共和国招标投标法》等法律法规的相关规定。此外,《中华人民共和国矿产资源法》及其实施细则对如何办理采矿许可证及矿产资源补偿费的征收作了规定[2]。但是这些法律涉及采砂管理的条款较少,针对性和可操作性不强,难以适应当前的管理形势[3]。

1.2 现行主要交易模式

河道采砂许可,是水行政主管部门根据公民、法人或者其他组织的申请,经必要的技术分析论证,在确保河势稳定、防洪和航运安全等的前提下,经审查批准后,准予其按许可的开采方式,在规划的可采区或保留区范围内从事一定数量的江砂开采的行政许可[4]。邓涌涌和江莹[5]认为以竞争方式实行河道采砂许可主要包括招标和拍卖,但不是唯一方式。梁荆江[6]则在分析前两种方式的基础上对现行的直接许可模式进行了阐述。结合当前形势可知,目前我国现行的河道采砂交易主要由招标、拍卖和直接许可三种方式组成,其概念和优缺点如表1所示。

表1 河道采砂主要交易模式及优缺点比较

2 交易模式选择模型

2.1 选择采砂交易模式的主要原则

对于河道采砂交易模式的选择,应切实遵循以下五项原则:

(1)公共安全和可持续利用优先原则。河道采砂应当以保证河势稳定、防洪安全、通航安全、水生态环境为前提,在避免自然环境破坏、服务功能下降,生物多样性降低的不良影响[7]并站在人与自然和谐共存的基础上,考虑代际间的可持续利用。

(2)公开、公平、公正、透明原则。河道采砂应在市场竞争机制下应当适度遵循市场的规律,采取公开、公平、公正、透明的方式进行许可。

(3)适应不同开采环境和市场环境原则。河道采砂交易方式的选择应当因地制宜地确定,符合采砂河段所在地的自然背景和市场背景。

(4)许可和监管兼顾原则。有效监管是保证所选交易模式有力执行的基础,因此必须坚持许可和监管兼顾的原则。

(5)合理收益原则。坚持合理收益原则,既可以避免砂石资源的无偿占用,又可以保证国有资源的正常收益。

2.2 交易模式选择模型的评价方法

河道采砂的交易模式选择属于备选方案的综合评价优选问题,由于开采条件和市场环境的动态不确定性,以及需要遵循的多项准则的约束,因此交易模式的选择属于多准则决策方法的应用范畴。在我国已有的工程交易模式选择研究中,王婷和唐德善[8]提出用模糊层次分析法对工程交易模式进行评价和决策,王学通和王要武则应用UEWAA算子和ULHA算子构建了基于可能度矩阵排序向量的决策支持模型[9],王卓甫、洪伟民和刘红梅等则针对现有工程交易模式决策模型中,准则权重的确定主观色彩过浓的现状,引入“熵权”的概念,对专家的主观权重进行修正[10],上述决策模型对工程交易模式的选择起到了积极作用,而河道采砂交易模式的选择由于涉及方众多、信息冗杂多变、且受政策影响较大,需要在充分发挥前人评价优势的基础上,引进处理模糊性和不确定性的方法,减少不必要的评价准则和人为设定属性的干扰,从而更准确地对备选方案进行综合评价。笔者在综合考虑上述因素的前提下,保留了“熵权”的客观修正优势,引入了有效处理模糊不确定性的粗糙集理论和三角模糊数的排序原理,建立基于粗糙熵权的模糊多准则决策模型以用于采砂交易模式的选择。

2.2.1 粗糙熵的定义

粗糙集理论是一种新的处理模糊和不确定知识的数学工具[11]。一般而言,一个系统中熵的存在总是同系统的相关因素和状态相联系,系统熵的大小表示该系统偏离平衡态的程度。熵是度量不确定性的最佳的工具和尺度[12]。粗糙熵的定义为:

定义1 四元组S=(U,R,V,f)是一个信息系统。其中:U为对象的非空有限集即论域;R为属性的非空有限集;V:Vα为属性α的值域;f:U×R→V为信息函数,它为每个对象的每个属性赋予一个信息值,即对于任意a∈R,x∈U,f(x,α)∈Vα。

P⊆R为U上的一个等价关系集合,P在U上导出的划分为U/IND(P)={X1,X2,…,Xn},则P的粗糙熵定义为:

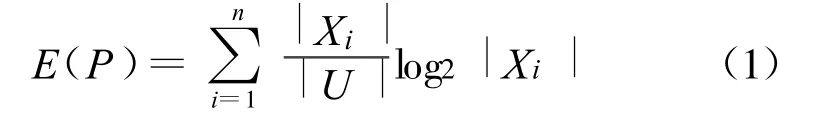
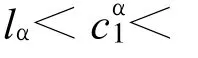
定义2 设S=(U,R,V,f)是一个信息系统,X⊆U,属性α∈R在R中的重要性Sig(α,R)定义为R中去掉α后所引起的粗糙熵变化大小,即

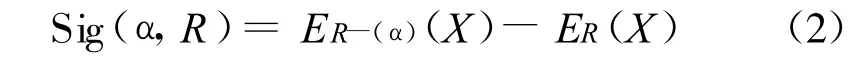
属性a∈R在R中是必要的,当且仅当Sig(α,R)＞0。又令属性集R的核CORE(R)={α∈R|sig(α,R)＞0}[14]。

2.2.2 模糊数的排序

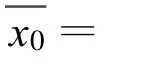
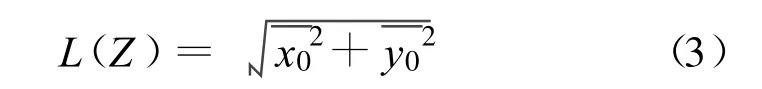
2.2.3 备选方案的评价矩阵

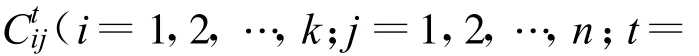
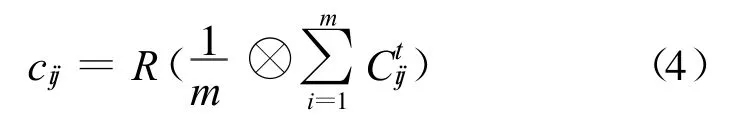
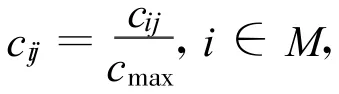
2.2.4 评价准则的权重处理

粗糙集能够进行属性约简,消除多余或相对次要的属性。多余属性的约简是指设Q⊆P,如果Q是独立的,并且IND(Q)=IND(P),则称Q为P的一个约简,即约简后不影响对原系统的表达[16]。结合常规模糊综合评判的权重确定方法使用如下准则:

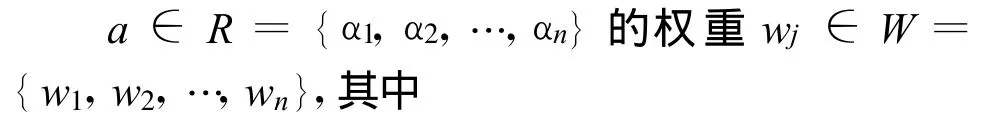
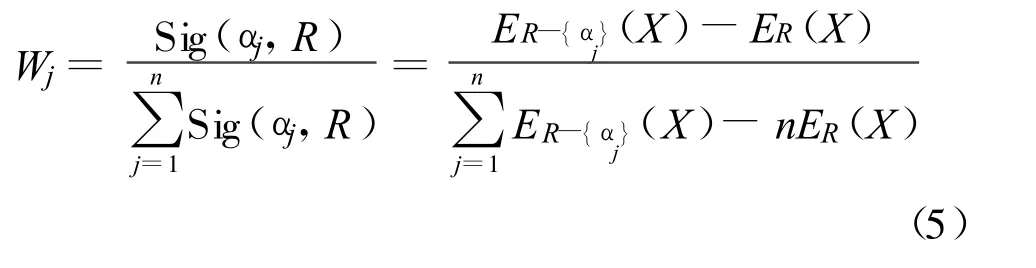
2.2.5 备选方案的最终选择

运用改进的TOPSIS法计算每个方案的正理想点与负理想点的距离以及每个方案的相对接近度,并根据贴近度进行排序。

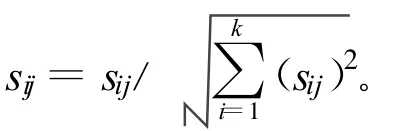
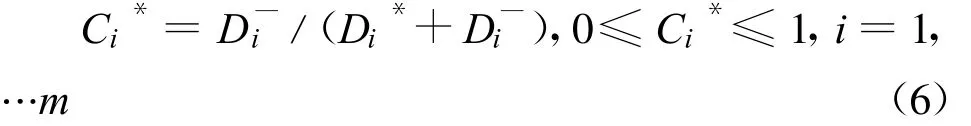
排列方案的优先次序,按Ci*由大到小排列,相对接近度最大的方案优先采用。

3 实例分析

鄂赣边界河段:左岸上起湖北省武穴市李顶武村(3304302,39355558),下至湖北省武穴市龙坪镇(3306223,39374786)。右岸上起江西省瑞昌市下巢湖闸(3302950,39355000)下至江西省九江县城子镇(3303000,39373650);其可采区属于长江水利委员会在省级边界确定的重点河段可采区,在《长江中下游干流河道采砂规划修编环境影响报告书》中,如图1所示。鄂赣边界重点河段江砂开采始于20世纪70年代末至80年代初,多年来一直是长江中下游干流河道的主要采砂河段之一,湖北省武穴市与江西省瑞昌市在该河段江砂开采的权属上一直各执已见,多次导致采砂纠纷。《长江河道采砂管理条例》规定长江水利委员会在省级边界重点河段直接承担河道采砂的审批、发证、收费及现场监管等管理责任。由于该河段长期以来就是敏感复杂河段,因此选择合适的交易许可模式迫在眉睫。

3.1 构建河道采砂许可层次结构模型

河道采砂许可方式的层次结构模型的建立必须以前述的五项原则为前提,结合采砂河段所位于的不同河道、不同开采条件和不同市场环境条件进行建立。该案例构建了如图2所示的采砂许可层次结构模型,最高的目标层即最合适的交易模式。第二层为准则层,依据文献[1-6]对河道采砂交易模式决策影响因素的探讨,将影响因素归纳为环境、利益和运作3个方面,其中环境包括河段历史背景、政策环境、市场环境3个指标,利益包括国家利益、地方利益、企业利益、后代利益等4个指标,运作包括公开透明、许可成本、人为干扰和利于监管等4个指标,最底层为方案层,即可供选择的3种交易模式。

图1 鄂赣边界可采区重点河段示意图

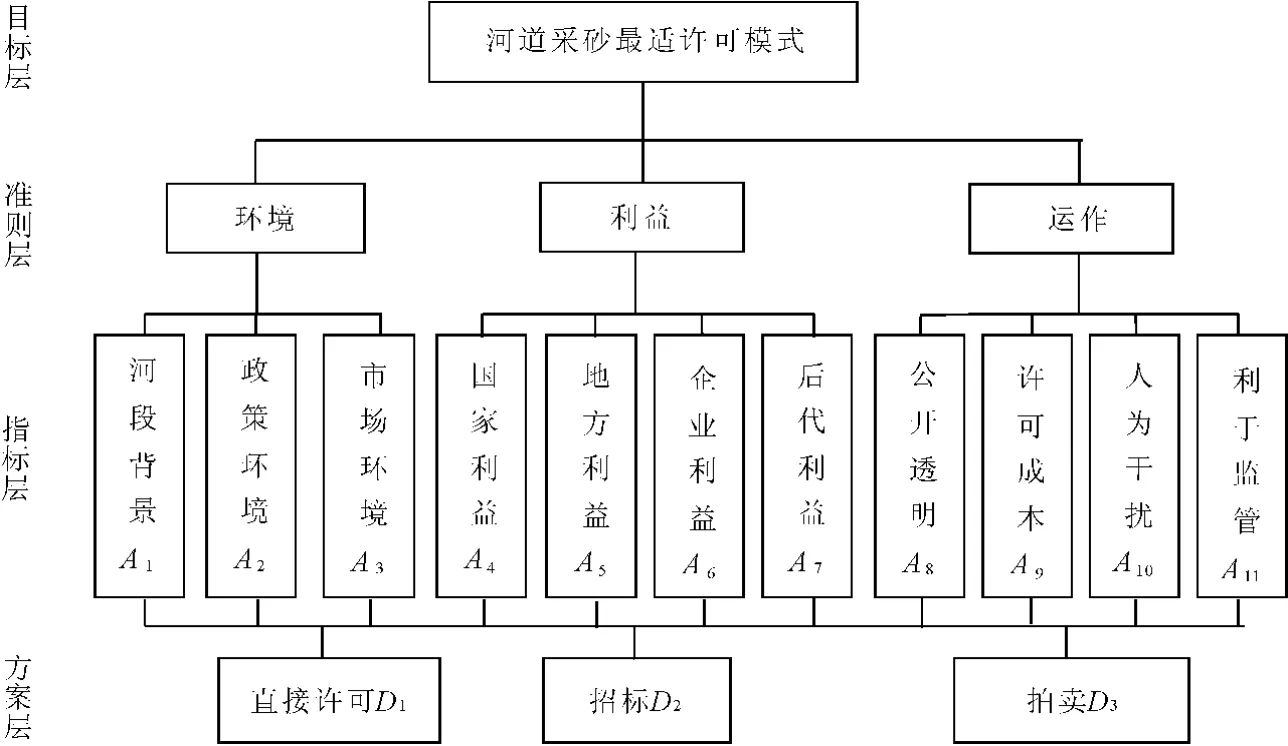
图2 河道采砂交易模式选择层次结构模型

3.2 构建备选方案的模糊评价矩阵

邀请若干位专家对备选方案在各评价准则下使用模糊语言集进行模糊综合评判,备选方案的模糊矩阵如表2所示。

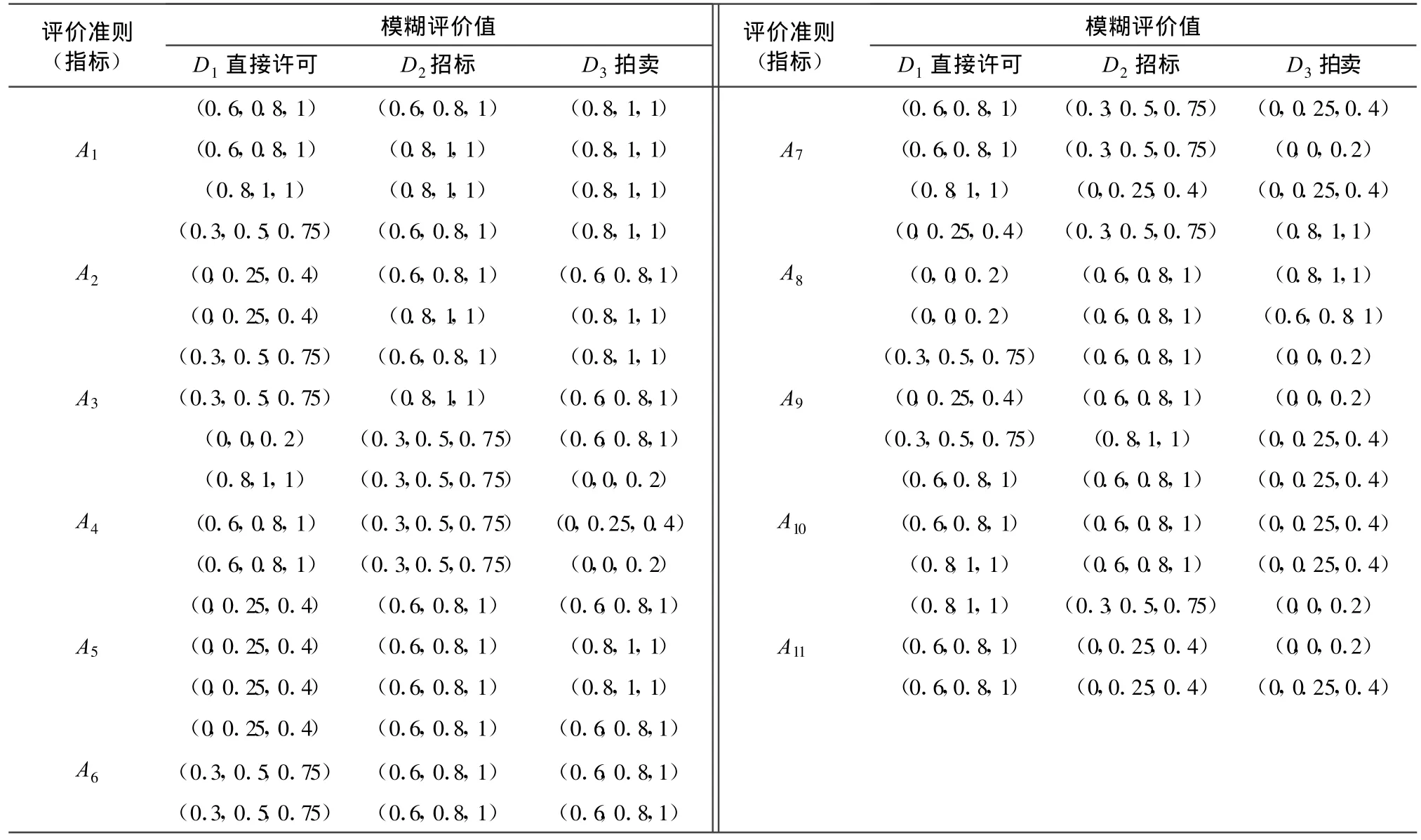
表2 备选方案的模糊评价

根据上述模糊评价矩阵,采用三角模糊数排序法,用距离L(Z)表示三角模糊数Z得到表3,并且根据效益型和成本型指标做适当处理得到备选方案的评价矩阵,如表4所示。

表3 三角模糊评价值对应的距离表示数

表4 采砂交易模式备选方案的评价矩阵

3.3 属性约简和权重确定

各指标评语集的三角模糊数距离表示为R(VP)=0.3399,R(P)=0.7162,R(F)=0.5620,R(G)=0.943,R(VG)=0.9957。属性Aj∈ {A1,A2,…A11},其值域VAj={[0.3399,0.5620)∪[0.5620,0.7162)∪[0.7162,0.9434)∪[0.9434,0.9957]},并且系统中,当信息函数f(xi,Ai)∈[0.3399,0.5620) 时 ,f′(xi,Ai)=1;f(xi,Ai) ∈[0.5620,0.7162) 时 ,f′(xi,Ai)=2;f(xi,Ai) ∈[0.7162,0.9434) 时 ,f′(xi,Ai)=3;f(xi,Ai) ∈[0.9434,0.9957]时,f′(xi,Ai)=4,xi∈X={x1,x2,x3}。通过离散化,可以确定采砂交易模式的评价信息系统S=(U,R,V′,f′)如表5所示,其中D4,D5,D6,D7,D8,D9表示已经付诸实施的成功采砂交易方案,其属性值结果为已知。

对属性集A={A1,A2,…,A11}进行约简得到{A1,A4,A7,A8}是其中的一个约简,选择R={A1,A4,A7,A8}作为备选方案的评价集,根据公式(2)解得,Sig(A1,A)=0.222,Sig(A4,A)=0.306,Sig(A7,A)=0.222,Sig(A8,A)=0.306,再由公式(5)解得各指标权重为W={0.210,0.290,0.210,0.290}。

3.4 备选方案排序选择

建立河道采砂交易备选方案的综合评价优选矩阵,如下表6所示。

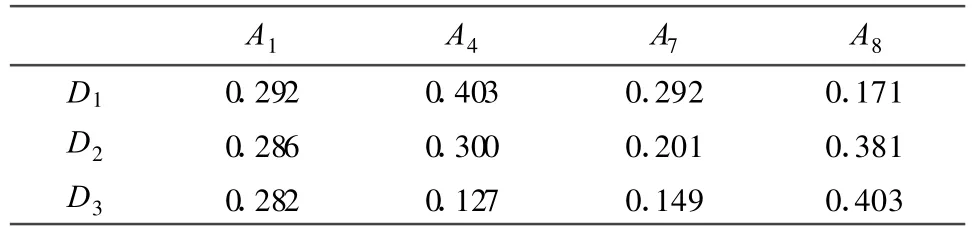
表6 河道采砂备选方案综合评价优选矩阵

由表可知正负理想点分别为sj*={0.292,0.403,0.292,0.403},sj-={0.282,0.127,0.149,0.171},相对接近度C1*=0.573,C2*=0.676,C3*=0.572。故该地区采砂交易模式的三种许可方案相对接近度排序为C3*＜C1*＜C2*,所以该河段可采区交易许可模式的最佳方案为D2,即招标模式。

4 结 语

河道采砂交易模式还除上述列举的三种以外,还有摇号、挂牌等形式,实质均为直接许可、招标和拍卖的不同组合。当前河道采砂交易模式顺应市场环境,引入了市场竞争机制的采砂许可,丰富了采砂许可模式,但是任何采砂许可都应在保证防洪、河势、生态等公共安全要求的基础上进行。与此同时,交易机制的优化既要借助机制设计理论和交易费用理论的指导,实现激励相容与合理收益,也应当遵循河道采砂许可维护河道的初衷,并力求采取有效的监管来保证采砂交易机制的顺利运行。

[1]王金生.河道采砂与管理[M].北京:中国水利水电出版社,2006:1.

[2]袁杰锋,刘振胜.长江河道采砂管理政策法规研究[J].人民长江,2000,31(11):22-23.

[3]侯良泽.河道采砂管理工作存在的问题及对策[J].中国水利,2011,(10):27-34.

[4]周建春.长江河道采砂许可性质和方式选择[J].人民长江,2008,39(12):87-89.

[5]邓涌涌,江 莹.浅析以竞争方式实施河道采砂许可[J].人民长江,2006,37(10):36-38.

[6]梁荆江.对长江河道可采区采砂经营权许可方式的思考[J].人民长江,2006,37(10):33-35.

[7]叶碎高,王帅,张锦娟.河道植物措施与生物多样性研究进展与展望[J].水利与建筑工程学报,2008,6(2):41-43.

[8]王婷,唐德善.基于FAHP法的工程交易模式评价与决策[J].水利科技与经济,2011,17(1):33-35.

[9]王学通,王要武.基于不确定多属性理论的总承包工程交易模式决策模型研究[J].中国软科学,2010,(2):153-160.

[10]洪伟民,刘红梅,王卓甫.基于熵权模糊综合评判法的工程交易模式决策[J].科技管理研究,2010,30(3):123-125.

[11]张文修,吴伟志,等.粗糙集理论与方法[M].北京:科学出版社,2004:13.

[12]邱菀华.管理决策与应用熵学[M].北京:机械工业出版社,2002:6.

[13]李鸿.一种基于粗糙熵的知识约简算法[J].计算机工程与应用,2005,41(14):78-80.

[14]崔广斌,李一军.基于粗糙熵权的模糊多准则决策方法及应用[J].控制与决策,2007,22(4):408-412.

[15]雷丽彩,周晶,李民.基于相对熵原理的大型工程项目交互式多属性群决策方法研究[J].中国软科学,2011,(2):166-174.

[16]张磊.基于粗糙熵的数据约简算法及应用研究[D].苏州:苏州大学,2007.

Study on Selection of River Sand Mining Modes Based on Rough Entropy Fuzzy Decision Model——Taking Workable Sector of E and Gan for Example

YANG Gao-sheng,XU Xin,LIANG Yu-ling,ZHANG Xiao-jin
(Engineering Management Institute of Hohai University,Nanjing,Jiangsu211100,China)

On the basis of the analysis of policy background and trading status of China's river sand mining modes,the optimized model of sandmining is established based on rough entropy fuzzy decisionmodel for three modes such as direct permission,bidding and auction.Through applying the model to select the sand mining modes in the workable sector of E and Gan,it is shown that the best mode for this area is bidding.In conclusion,the rough entropy fuzzy decision could follow the basic principles of sand transaction,and the method is feasible and effective for the selection of sand mining modes.

river sand mining;transaction model;rough entropy;fuzzy decision;public resources

TV148

A

1672—1144(2012)01—0012—06

2011-10-14

2011-12-01

水利部公益性行业科研专项经费项目(201001007-01)

杨高升(1966—),男(汉族),江苏高淳人,博士,副教授,主要从事工程项目管理研究。