水面舰船规范中甲板纵骨稳定性校核的差异研究

王晓强 陈 崧 李陈峰 任慧龙

1中国舰船研究设计中心军事代表室，湖北武汉430064 2哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨150001

水面舰船规范中甲板纵骨稳定性校核的差异研究

王晓强1陈 崧1李陈峰2任慧龙2

1中国舰船研究设计中心军事代表室，湖北武汉430064 2哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨150001

甲板纵骨的稳定性问题是水面舰船结构设计中的一个重要问题。《舰船通用规范》和《水面舰艇结构设计计算方法》对纵骨带板折减系数取法的差异有时会导致工程中出现不同的结果。从理论上分析了《舰船通用规范》和《水面舰艇结构设计计算方法》对纵骨屈曲分析评估方法的差异，并用数值算例结果给予说明。研究结果为：《舰船通用规范》中的稳定性校核标准较《水面舰艇结构设计计算方法》严格，对于理解和修订国军标以及保证舰船结构安全有一定的理论意义和实用价值。

水面舰艇；国军标；纵骨；稳定性；极限状态

1 引言

结构稳定性是指在承受轴向压缩荷载时能够保持结构初始形状的能力。以甲板结构为例，在中垂状态下，甲板承受较大的轴向压力，其稳定性问题就显得较为突出，一旦丧失稳定性，必将导致整个结构的破坏，且失稳失效往往先于屈服失效出现。因此，船舶结构稳定性问题是船舶结构设计中的重要问题［1－2］。 随着高强度钢的广泛应用，同样载荷下的船体结构厚度减小，刚度随之降低，结构的稳定性问题就显得更为突出。

通过广大学者近30年的努力，目前在板架和加筋板稳定性的计算方法、试验研究等方面取得了不少成果，有些成果已纳入水面舰艇设计规范。规范中关于结构稳定性校核的条款采用的理论和方法基本一致，均参照前苏联提出的欧拉应力修正曲线的临界应力校核方法，但有效带板宽度的计算或带板折减系数的选取存在一定的差异，这就会导致纵骨的稳定性校核有时不能同时满足多个规范的要求。

本文从船体强度及稳定性理论出发，推导纵骨稳定性校核的相关公式与参数，分析折减系数产生差异的原因和影响，为水面舰艇结构设计及稳定性校核提供一些参考。

2 杆件稳定性理论

研究结构的稳定性应求出其临界应力，使该值不小于所受的压应力，使结构能正常工作。

对于两端简支的单跨梁，其欧拉应力σE的计算公式为：

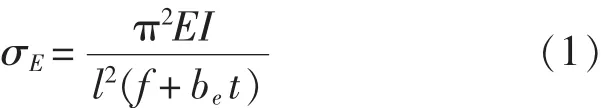
目前水面舰船结构设计与计算常用的2项规范——《舰船通用规范》（简称GJB4000－2000）和《水面舰艇结构设计计算方法》（简称GJB／Z119－99），对于纵骨稳定性校核的方法基本一致，其主要条款要求如下：

式中，b为纵骨间距；φ为折减系数，变化范围是0＜φ≤1，当 φ＞1时，取 φ＝1。

按式（1）求得的欧拉应力σE为构件在弹性范围内失稳的应力。事实上，压杆在失稳时材料可能已超过弹性范围，并且实践也表明超过弹性范围时失稳的力远小于欧拉应力。通常将构件在弹性范围外失稳的应力叫作临界应力或屈曲应力σcr。临界应力σcr是结构从初始形状向其他形状突变时的平均应力，取决于结构的尺寸、形状、材料和所受压力分布模式，是一个结构的固有值。

临界应力σcr的计算方法主要有欧拉应力修正法和基于切线理论的方法。欧拉应力修正法是目前常用的一种方法，计算结果如图1中实线所示。

式中，E为材料弹性模量；I为包括带板的骨材剖面惯性矩；l为骨材跨距；f为骨材本身剖面积；be为有效带板宽度；t为带板厚度；σE为纵骨欧拉应力；σe为板材的欧拉应力。

带板有效宽度计算公式为：

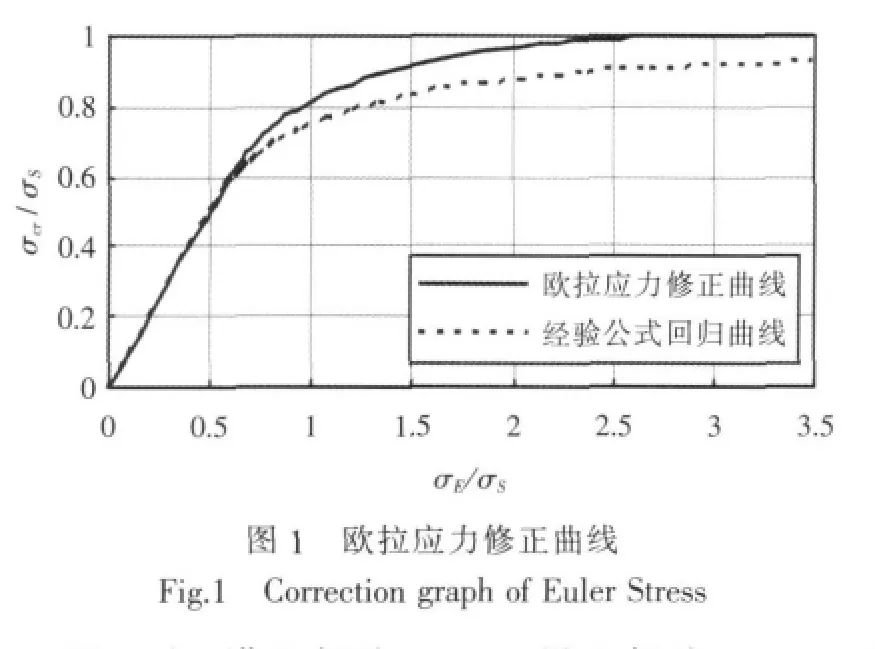
图 1 中，横坐标为 σE／σS，纵坐标为 σcr／σS，σS为材料屈服极限。 当 σE／σS≤0.5 时，σcr≈σE；当σE／σS＝2.5 时，σcr／σS＝0.99。对该修正曲线进行处理，即可得到工程上常用的临界应力σcr的计算公式：

图1中的虚线根据式（3）计算得到，可以发现：该公式计算简便，且当构件的欧拉应力σE较小时，求得的临界应力σcr与试验值（欧拉应力修正曲线值）拟合较好；但当构件的欧拉应力σE较大时，临界应力 σcr较试验值小（当 σE／σS＝2.5 时，σcr／σS＝0.9）。因此，该公式对于较强杆件的稳定性校核偏于保守。

3 国军标中纵骨稳定性校核的要求

1）强力甲板、舷顶列板以及船底板上的骨架构件中的带板纵骨，在肿部0.5倍设计水线长范围内，其欧拉应力与其所用材料的屈服应力之比值大于 2.0、在端部大于 1.5。

2）在初步设计时建议受压纵骨的带板宽度的取法为：在计算带板纵骨剖面惯性矩i时，取纵骨间距，但不超过1／6的纵骨跨距；在计算带板纵骨剖面面积 f时，取 0.5b（1＋φ）。其中，b 为纵骨间距，φ为板的折减系数，当φ大于1时取φ等于1。

在此基础上，计算带板纵骨的惯性矩和剖面积，根据式（1）求得弹性范围的欧拉应力σE，而后按欧拉应力修正曲线折算临界应力，进而完成纵骨的稳定性校核。

需要指出的是，在计算带板折减系数φ时，2项规范出现了差异。其中，GJB4000－2000中提出φ为板的欧拉应力与作用在板上的压缩应力的比值，对于不计甲板荷重的上甲板的欧拉应力为σe，则其上的甲板纵骨的折减系数为：φ ＝σe／σ1；而GJB／Z119－99中提出φ为板的欧拉应力与板材屈服应力的比值，即φ＝σe／σS。2项规范中对于折减系数的这一细微差异，却给广大舰船设计人员带来了困扰，因为实际应用表明，有时对满足《水面舰艇结构设计计算方法》的纵骨采用《舰船通用规范》进行稳定性复核时，结果却不满足。

4 带板折减系数的差异分析

现以甲板纵骨的稳定性校核为例，对规范中相关公式进行推导，以期对带板折减方法的差异及其影响作出分析和讨论。

中垂状态下，甲板承受着较大的总纵弯曲轴向压力，一旦甲板失稳，则必将导致整个船体结构的破坏，船体出现极限状态。对于船体梁而言，可能存在以下 3 种极限状态［3-5］：

1）最大承载能力的极限状态。如果此时的外载荷再增加，船体就将出现整体毁坏，其中包括剖面屈服破坏和板架屈曲破坏2种模式。

2）正常使用的极限状态。如果此时的外载荷再增加，虽然船体尚未出现整体毁坏，但由于过大的变形或剧烈的振动等原因已无法正常使用。

3）维持足够使用寿命的极限状态。如果此时外载荷再增加，虽然船体未出现整体毁坏，也能正常工作，但由于疲劳损伤已无法使船体达到预定的使用年限。

若依照上述分类可以看出：纵骨失稳对应的是最大承载能力的极限状态和正常使用的极限状态。

4.1 正常使用极限状态时的差异分析

将GJB4000-2000和GJB／Z119-99规范中上甲板的折减系数和带板纵骨的欧拉应力分别记为φ1、φ2和 σE1、σE2，其中 φ1= σe／σ1，φ2=σe／σS。

对于水面舰艇的结构设计与计算，在正常航行状态下，无论中垂或中拱情况，总纵弯曲应力σ1均需满足下式：

同理，根据国军标中船体梁极限强度要求，可得第一次近似计算的总弯曲应力为：

式中，η 为折减系数，一般取η ＝0.8～1.0；σS为板材的屈服强度；σe为板材的欧拉应力。则：

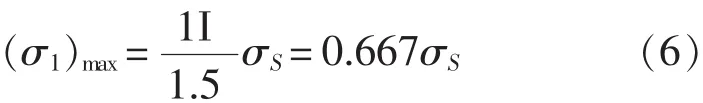
考虑到砰击载荷作用下局部构件可能失稳，根据极限弯矩校核中等值梁剖面系数逐步近似计算之 “后一次计算与前一次计算的总弯曲应力差值不超过5%”的要求，即：

则：

因此，可得：

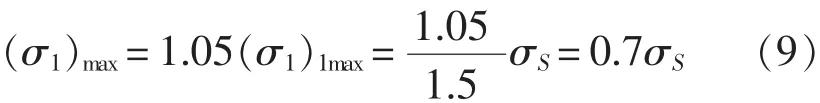
因此，不论何种情况，σ1＜σS。在板材的欧拉应力相同的情况下，φ1肯定大于φ2，即根据《舰船通用规范》计算的带板折减系数较大。

对于带板纵骨的欧拉应力σE计算而言，由于在计算剖面惯性矩I时，2项规范的带板取法相同，因此i一致。但在计算剖面积时，由于2项规范在带板折减系数的取法上不同，且φ1＞φ2，因此根据《水面舰艇结构设计计算方法》获得的带板纵骨剖面积较大，导致欧拉应力σE2小于σE1，即《舰船通用规范》中对纵骨稳定性的要求更为严格。上述差异导致的后果是在实际的水面舰船结构设计与纵骨稳定性校核时，按照《水面舰艇结构设计计算方法》设计的纵骨在采用《舰船通用规范》进行复核计算时，稳定性有时会不满足。

4.2 最大承载能力极限状态时的差异分析

以上讨论的都是在正常航行时甲板纵骨的稳定性，而对于最大承载能力的极限状态，即通常意义上的极限状态，此时甲板结构的总正应力接近材料屈服限，即：

此时，根据2项规范得到的带板折减系数和带板纵骨的欧拉应力基本一致，因此甲板纵骨的稳定性校核结论保持一致。

5 算例验证与分析

为了验证上述2项标准之间的差异，以某型舰的纵骨架式艏部甲板纵骨稳定性计算为实例来加以考核。

5.1 原始数据及材料

纵骨间距b＝390 mm，纵骨跨距l＝950 mm，甲板板和纵骨的材料屈服强度均为σS＝400 MPa。

5.2 稳定性计算

带板欧拉应力的计算公式为：

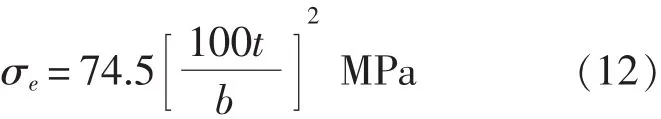
式中，t为板厚，mm；b 为纵骨间距，mm。

经计算得到的中剖面的甲板板的总纵弯曲压应力最大值为 σ1=78.8 MPa。

计算纵骨稳定性时，要对纵骨的带板进行失稳折减：GJB4000-2000规定的折减系数为φ1=σe／σ1，GJB／Z119-99 规定的折减系数为 φ2=σe／σS。纵骨带板折减系数如表1所示，当折减系数大于1时，取1。

纵骨的理论欧拉应力按（1）式进行计算，并结合GJB4000-2000 （简记为 G1） 和GJB／Z119-99（简记为G2）中关于纵骨稳定性计算时的带板宽度取值方法，即可得到纵骨的理论欧拉应力σE，进而得到纵骨的稳定性校核参数ψ＝σE／σS，对于艏部的纵骨稳定性，当ψ＞1.5时满足规范要求。

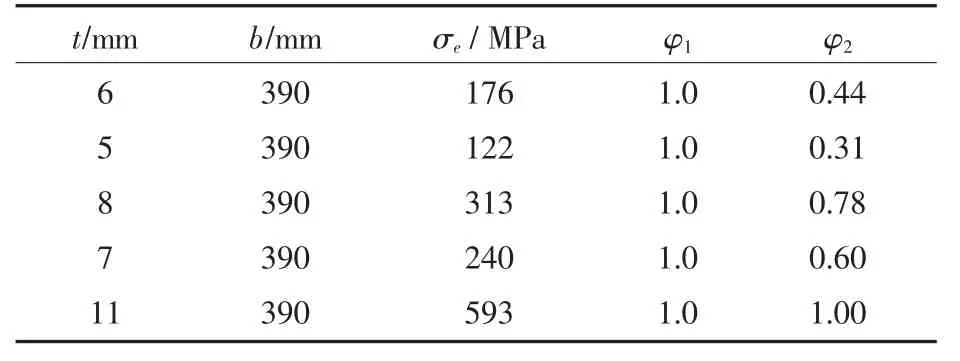
表1 纵骨带板折减系数计算Tab 1 Calculation of longitudinal band plate reduction coefficient

表2 纵骨欧拉应力计算Tab 2 Calculation of longitudinal Euler stress

5.3 纵骨的稳定性对比分析

将表2中的ψ值绘制成图，如图2所示，从中可以清晰地看到：

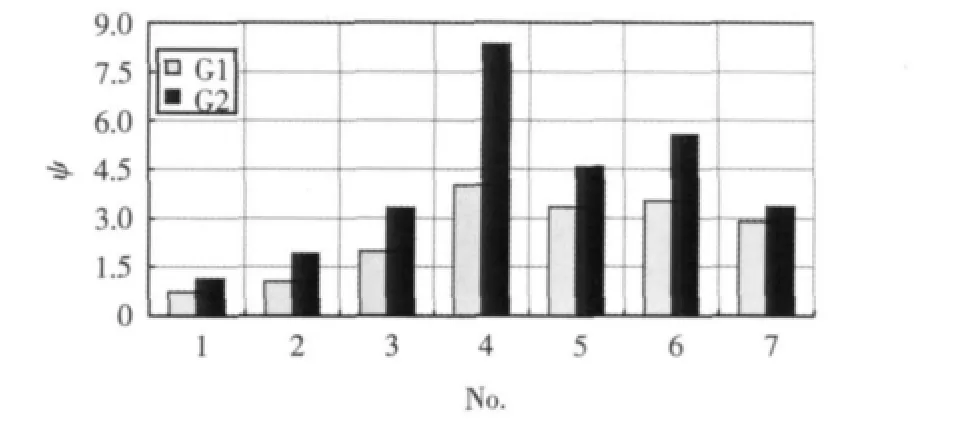
图2 纵骨稳定性校核参数对比简图Fig.2 Comparison of longitudinal stability check parameters

1）根据G1和G2计算得到的ψ值有着明显的差异，且前者计算的值要大于后者；

2） 根据 G1 得到的计算值，No.1、No.2 均不满足规范要求，因此，将5＃、5.5＃球扁钢均更换为7＃，就能满足规范要求；

3）根据G2得到的计算值，No.1不满足规范要求，因此，要将 5＃ 球扁钢均更换为 5.5＃，就能够满足规范要求；

4）分别根据G1和G2得到的No.2得到不同的结论，这就导致了规范之间的矛盾。

6 结 语

1）《舰船通用规范》和《水面舰艇结构设计计算方法》中纵骨稳定性校核的基本理论一致，常用的方法是基于欧拉应力修正曲线的临界应力法，该方法只是一种近似方法，只有直接应用材料的压缩应力－应变曲线来描述材料的非线性影响才能得到更精确的解。

2）由于带板折减系数的取法不同，因此通常情况下，《舰船通用规范》中的稳定性校核标准较《水面舰艇结构设计计算方法》严格。

3）在总纵弯曲强度不明确时，可以采用《水面舰艇结构设计计算方法》可对纵骨稳定性进行初步校核，当总纵强度明确时，采用《舰船通用规范》计算纵骨稳定性的安全性较高。

［1］俞铭华.船舶板架稳定性研究进展［J］.华东船舶工业学院学报.2000，14（4）：20－25.

YU M H.Advances in stability analysis of ship grillages［J］.Journal of East China Shipbuilding Institute，2000，14（4）：20－25.

［2］曾晓辉，戴仰山.单向压力作用下有初挠度矩形板的有效宽度和减缩有效宽度［J］.中国造船，1998，39（3）：57－65.

ZENG X H， DAI Y S.Effective width and reduced effective width of a rectangular plate with initial deflection under uniaxial compression［J］.Shipbuilding of China，1998，39（3）： 57－65.

［3］戴仰山，沈进威，宋竞正.极限强度校核中的几个问题［J］.中国造船，2007，48（1）：102－105.

DAI Y S，SHEN J W，SONG J Z.Some questions in ship ultimate strength analysis［J］.Shipbuilding of China，2007，48（1）：102－105.

［4］吴广明.用ANSYS进行甲板板架稳定性计算［J］.中国舰船研究，2007，2（2）：5－8.

WU G M.Stability calculation of deck grillage using ANSYS software［J］.Chinese Journal of Ship Research，2007，2（2）：5－8.

［5］郭达，谢祚水，俞铭华.大型板架稳定性的有限元分析［J］.华东船舶工业学院学报，2000，14（2）：14－18.

GUO D， XIE Z S， YU M H.Program design of calculating the stability of the grillage of large－sized carrier by the finite element method［J］.Journal of East China Shipbuilding Institute，2000，14（2）：14－18.

Difference of Deck Longitudinal Stability Check Between GJB4000-2000 and GJB/Z119-99

Wang Xiao－qiang1Chen Song1Li Chen－feng2Ren Hui－long2

1 Naval Military Representative Office in China Ship Development and Design Center， Wuhan 430064， China 2 College of Shipbuilding Engineering， Harbin Engineering University， Harbin 150001， China

Deck longitudinal stability problem is an important issue for surface warship＇s structure design.Different methods in determining the longitudinal band plate reduction coefficient according to the standard of Ship General Specifications （SGS， GJB4000－2000） and Structure Design and Calculation Method for Surface Ship （SDCM，GJB／Z119－99）maybe lead to different conclusions.Differences between these two national military standards were analyzed by theory and explained by numerical computation examples.Results show that the standard of SGS is more strict than SDCM.

surface warship； national military standards； longitudinal； stability； limit state

U661.43

A

1673－3185（2012）02－56－04

10.3969/j.issn.1673-3185.2012.02.010

2011-10-10

王晓强（1981－），男，博士。研究方向：舰船总体。E-mail：wxq11211＠163.com

王晓强。

［责任编辑：张智鹏］