一种判定离散系统因果性的有效方法*

谢小娟，何国栋，冯友宏

(安徽师范大学，安徽 芜湖241000)

在“信号与系统”和“数字信号处理”的本科教学中，对系统的研究往往约束于线性时不变(LTI:linear time invariant)系统，而对此类系统可以用线性常系数差分方程来进行系统的输入输出关系描述。在各种版本的教材中都明确指出:线性常系数差分方程描述的系统不一定是线性非时变系统，同样也不一定是因果的系统，这和系统的初始状态(边界条件)有直接的关系［1-3］。本文将从一个经典的实例为出发点，阐述线性常系数差分方程与系统的线性非时变性及因果性的关系，并重点讨论线性常系数差分方程描述的LTI系统的因果性判定方法，从而有效地加深初学者对此类问题的理解和掌握。

1 常系数差分方程所描述系统线性非时变性及因果性讨论

如果系统满足线性常系数差分方程，则它也满足构成线性非时变系统的必要条件。以下给定一个典型的线性常系数差分方程如式(1)所示，来讨论常系数差分方程描述的系统是否一定具有线性非时变性及因果性。之所以典型是因为该方程在［1］，［2］，［3］，［4］等教材中都有采用以说明线性常系数差分方程与系统稳定性、因果性的关系，只不过各教材给出的初始条件及所说明的问题侧重点不同而已。本文对各教材的讨论进行了综述，共给出了6种初始条件，以更清晰而全面地揭示问题的本质。

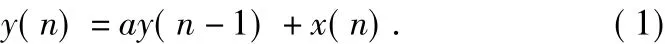
式(1)差分方程所描述的系统被看成一个黑盒子，我们只是知道系统即时输出y(n)可以从即时输入值x(n)和上一个输出值y(n－1)计算得到。至于系统是否为线性非时变的，是否为因果的，需要结合系统的初始条件来进行判定。以下给定六种不同的初始条件，分别来进行判定:

(1)y(0)=1;(2)y(－1)=1;(3)y(0)=0;

(4)y( －1)=0;(5)y(n)=0，n＜0;

(6)y(n)=0，n ＞0.

(1)初始条件为y(0)=1时，可以判定系统为非线性、移变系统。根据线性非时变系统的定义［1］，证明如下:

因为x1(n)和x2(n)为移位关系，但y1(n)和y2(n)非移位关系，故系统是移变的。由上述推导可知:

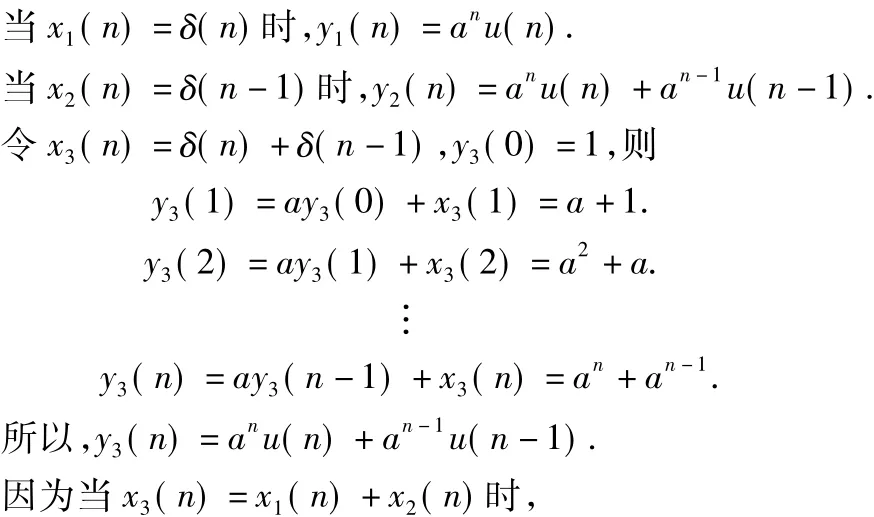
y3(n)≠y1(n)+y2(n)，故系统是非线性。综合可知系统为非LT1系统，证毕。

按照同样的方法，下面对剩余的5种情况也分别进行了判定。

(2)初始条件y(－1)=1时，系统为非线性，时变系统。若x1(n)=δ(n)，系统输出为:

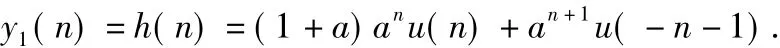
(3)初始条件为y(0)=0，此时系统为线性、时变系统。若x1(n)=δ(n)，系统的输出为:

(4)初始条件为y(－1)=0，此时系统为线性、非时变系统。若输入x1(n)=δ(n)，系统的输出为:

(5)初始条件为n＜0，y(n)=0，此时系统为LTI系统。输入x1(n)=δ(n)，系统的输出为y1(n)=h(n)=anu(n)。

(6)初始条件n＞0，y(n)=0，此时系统为LTI系统，输入x1(n)=δ(n)，系统的输出为y1(n)=h(n)= －anu(－n－1)。

对于上述六种情况，系统的因果性该如何判定呢?对于LTI离散系统，如果其具有因果性，则充分必要条件［1］为:

其中，h(n)为系统的单位取样响应，即当x(n)=δ(n)时的零状态响应y(n)=h(n)。在n=0时刻之前，及n＜0时无信号加入，故y(n)=0。

对于非LTI离散系统，不能用h(n)=0，n＜0来进行判定，此时要借助因果系统的定义来进行判断。因果系统的定义［1］为:若系统n时刻的输出，只取决于n时刻以及n时刻以前的输入序列，而与n时刻以后的输入无关，则称该系统为因果系统。如果按照定义进行因果性判定，必须要知道输入x(n)与输出y(n)的映射关系，即要知道输出y(n)关于输入x(n)的解析表达式:y(n)=f(x(n))。比如下面四个关系式:

此时可根据定义判定前三个关系式所描述的系统是因果，第四个是有条件因果系统(条件为k≥0)。而当系统的输入输出关系为差分方程给出，如式(1)所示，此时不能直接用定义加以判断，需要将(1)式变换为y(n)=f(x(n))的形式，再进行判定。而变换是否对所有常系数线性差分方程都可行尚且不论，若可以转换则过程必不简单，这也是本文有待深入研究的问题。故而对于由线性常系数差分方程描述的非LTI系统，其因果性的判定尚不确定，有待深入研究。

综合上述同一差分方程给定的六种初始条件，可以得到六个系统，其线性非时变性及因果性如表1所示。

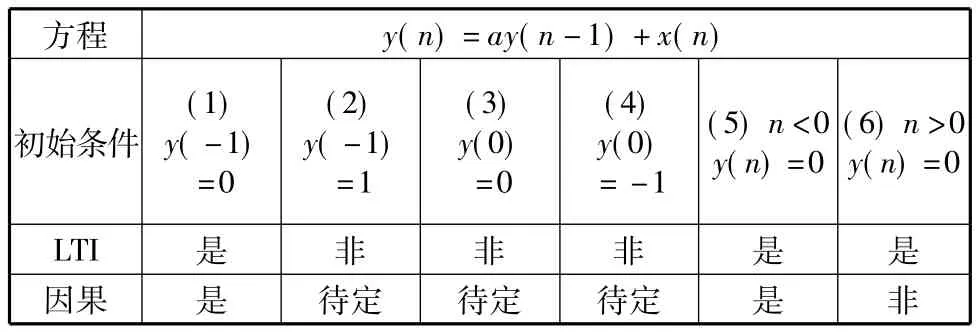
表1 六种系统的性能比较

从表格我们不难发现，对于一个差分方程，不同的初始条件，得到的系统性是不一样的。一个常系数线性差分方程并不一定代表因果系统，也不一定表示线性移不变系统。这些都由边界条件(初始)所决定。

2 判定LTI系统因果性的新方法

对于给定的常系数N阶差分方程

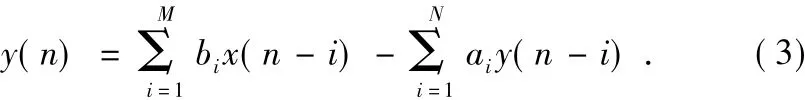
若根据初始条件，假定经过判定描述的是一个LTI系统，则必有如下结论:

如果初始条件为 y(n)=0，n＜0或 y(－1)、y(－2)、…、y(－N)皆为零，即系统无初始储能，处于零状态，则系统必为因果的。反之，如果y(－1)、y(－2)、…、y(－N)不全为零，则系统必为非因果的。证明如下:

若系统为LTI系统，则因果性判定如下:

由(2)式可知系统为因果系统，反之，y(n)=0，n＜0不成立，如 y( －2)=1，则

此时由(2)式可知，系统为非因果系统，证毕。

上述结论换句话说就是:对于差分方程描述的LTI系统，如果初始条件为0则为因果系统，反之为非因果系统。此结论可通过对上节讨论的六种情况来进行验证，其结果与表1所得结论是一致的。又由于在“信号和系统”以及“数字信号处理”的本科教学中，除了特别说明外，都假定:常系数线性差分方程就代表线性移不变系统，且多数代表因果系统。故而本文所提出的方法是非常简洁实用的。

3 结论

本文从一个典型的常系数差分方程出发，详细论证了一个常系数线性差分方程并不一定代表因果系统，也不一定表示线性移不变系统，这些都由边界条件(初始)所决定。同时对常系数线性差分方程描述的LTI系统，提出了一种有效判定因果性的方法。对于常系数线性差分方程描述的非LTI系统，其因果性的判定有待深入的研究。

［1］王世一.数字信号处理［M］.修订版.北京:北京理工大学出版社，2006.

［2］郑君里，应启珩，杨为理.信号与系统(下册)［M］.第2版.北京:高等教育出版社，2000.

［3］高西全，丁玉美.数字信号处理［M］.西安:西安电子科技大学出版社，2008.

［4］程佩青.数字信号处理教程［M］.第3版.北京:清华大学出版社，2007.