一种改进的安全两方矩阵计算协议

余景波，刘国林，曹振坦，崔 娟

(1.山东科技大学测绘科学与工程学院，山东青岛 266510;2.海岛(礁)测绘技术国家测绘局重点实验室，山东青岛 266510 3.山东省第四地质矿产勘查院，山东 潍坊 261021)

安全多方计算(Secure Multi－party Compulation)问题，是Yao［1］在1982年首先提出的。Goldreich，Micali和Wigderson等人［2］将其进行了进一步发展和推广。目前，多方安全计算问题一般性研究取得了很多成果［3－4］，但特殊问题研究［5－8］成果相对较少。本文只讨论安全两方计算(Secure Two－party Compulation)问题，其可定义为［9］是拥有秘密输入的两方，都希望用各自的秘密输入共同计算一个函数，计算要求每方都能接收到正确的输出(正确性)，并且每方只能了解自己的输出(保密性)。矩阵作为科学计算的一个基本工具，在计算机应用中显得十分重要。Du［10］和罗文俊［11］等人对两方安全矩阵计算协议进行了研究。

本文在安全两方计算环境下，利用安全两方向量加乘混算协议和安全两方矩阵加乘混算协议［12］基本思想，构造和改进了一种安全两方矩阵计算协议。

1 预备知识

参与者，就是提供输入，得到输出并且执行实际计算的各方。执行实际计算的参与者集合表示为P，所有参与者(包括输入，输出和计算)的集合表示为 ^P，P和^P户没必要一定相等，但是一定有P∈^P。

攻击者(或称敌手)，就是在可信多方计算协议中，企图破坏协议安全性或正确性的人。攻击者可以腐败参与者的一个子集。可以将攻击者看成一个电脑黑客，他可以破坏或控制参与者的计算机。

半诚实方(Semi－Honest Party):一个半诚实方将准确地完成协议，但是，同时记录下所有的中间结果，这些中间结果将用于推导额外的信息。

保密性(Privacy):任何一方都只能了解自己的信息。在实际过程中，其它一方的信息只能从自己的输入和输出中推得。

数据扰动假设(Data Perturbation assumption):如果一个输入x∈X，并且，r是一个均匀分布域F中的随机数，同时满足|F|≫|X|这个条件，那么x+r就可以有效地保护r的秘密信息。

2 改进的安全两方矩阵计算协议

2.1 协议的描述

假设协议的两个参与者是Alice和Bob，具体描述如下:

输入:Alice有一个n阶方阵Ra，两个n维列向量b11，b12;Bob有一个n阶方阵Rb，两个n维列向量b21，b22。

输出:Alice得到一个n维列向量r1，Bob得到一个n维列向量r2，满足r1+r2=Ra(b21+b22)+Rb(b11+b12)。

2.2 协议的具体流程

(1)Alice和Bob约定两个正整数p和m，同时让pm足够大，这样造成pm次n维方阵加法运算无法进行的。

(2)Alice和Bob协商三个公开的数q，g，h其中q是一个大素数，g，h均是Z*q的元素，并且任何人都不知道离散对数loggh。

(3)Alice和 Bob分别拥有私钥 zi和 ri，注册公钥分别为 yi=hzi和 ei=hri(i=1，…，p，zi≠ri)。

(4)Alice产生m个随机n阶方阵Ra1，…，Ram，使得Bob产生m个随机n阶方阵Rb1，…，Rbm，使得

(5)对每一个j=1，2，…，m，Alice和Bob执行下面的子步骤:

①Alice产生一个秘密随机数1≤k≤p，Bob产生一个秘密随机数1≤l≤p;

④Alice 随机选取 βi∈zq，用 Bob 的公钥 ei=hVi进行加密计算

Bob 随机选取 αi∈zq，用 Alice 的公钥 yi=hzi进行加密计算然后，Alice 将密文(Ai，Bi)通过公共信道发送给Bob，Bob将密文(Ci，Di)通过公共信道发送给Alice;

⑤Alice和Bob收到密文后，分别用自己的私钥计算出自己获得的数据信息

对自己获的n阶方阵数据信息进行验证(如果Alice和Bob都通过验证即⑥中两等式成立，说明Alice和Bob各自获得数据信息有效，反之，各自获得数据信息无效。Alice和Bob其中任何一人获得无效n阶矩阵数据，该协议停止执行);

⑦Alice和Bob对所有的i=1，2，…，p，都能通过⑥中公示验证，则表明:

Alice获得Bob发送的p个有效n阶方阵(H1，H2，…，Hp)，其中H1=Rbj，其余的(p－1)个Hi是随机n阶方阵(因为ι是一个秘密数据，只有Bob知道，而Alice不知道哪一个Hi是Rbj);Bob获得Alice发送的p个有效n阶方阵(G1，G2，…，Gp)，其中Gk=Raj，其余的(p－1)个Gi是随机n阶矩阵(因为k是一个秘密数据，只有Alice知道，而Bob不知道哪一个Gi是Raj)。

⑧对所有的 i=1，2…，p，，Alice 计算 Hj，i=Hi(b11+b12)+hj，其中 hj是随机 n 维列向量，而 Bob 计算Gj，i=Gi(b21+b22)+gj，其中 gj是随机 n 维列向量;

3 协议分析

3.1 正确性分析

(1)协议执行后，Alice和Bob分别得到n维列向量r1和r2，可以得:

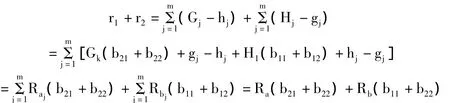
(2)在⑤中，Alice和Bob能用各自的私钥获得原明文，证明如下:

通过上述①和②的分析，就可以证明了Alice和Bob能够获得自己的明文。

(3)如果Alice和Bob都是诚实的，那么他们所发送对方的n阶方矩阵信息总有发送成功机会。

(4)如果Alice和Bob不诚实，他们发布虚假信息，可以通过⑥中公式进行验证;Alice和Bob其中有一个不诚实，也可以通过⑥中公式进行验证;攻击者发布的虚假信息也可以通过⑥中公式进行验证，从而减少了攻击者对该协议执行的危害。

(5)证明⑥中等式的正确性，方法如下:

3.2 安全性分析

(1)对每一个 j=1，2，…，m 来说:

① Bob猜对n维矩阵Raj的概率和Alice猜对n维矩阵Rbj的概率分别为，那么Bob猜对n维矩阵Ra的概率和Alicet猜对Rb的概率分别为，又因为Pm是一个足够大的数，所以的近值为零，由此可知Alice和Bob都不可能得到对方n维矩阵Ra和Rb的信息。

(2)Alice和Bob通过对方公钥加密算法对自己所发送的方阵信息进行加密，形成密文，然后通过公共信道传输，从而保证了数据传输过程中的安全性，这是计算上的安全性。

(3)攻击者获取了公共信道上的密文，如果没有Alice和Bob私钥，就不能用公式进行解密;如果攻击者利用已知的公钥yi=hzi和ei=hri来获取私钥zi和ri，相当于求解离散对数的困难性。

(4)攻击者伪造私钥，不能获得正确n阶方矩阵信息，证明如下:

①如果攻击者伪造私钥z＇i≠zi，也推导不出正确的ti，具体推导过程如下:

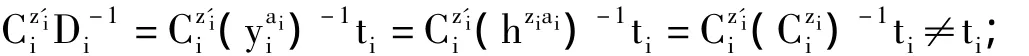
②攻击者如果伪造r＇i≠ri，也推导不出正确的si，具体过程如下:

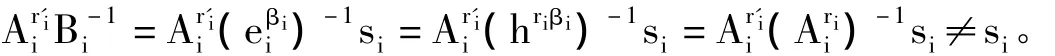
(6)由上面(5)中的分析，可以得到:

(7)因为每一个 Hi，Gi，hj和 gj(i=1，…，p，i≠k，i≠l;j=1，…，m)是随机 n 维矩阵和随机 n 维列向量，可以分别对b11+b12和b21+b22进行数据伪装(数据扰动假设)，避免数据信息泄露。

4 结束语

本文通过对改进的安全两方矩阵计算协议从正确性和安全性分析，可以得出:

(1)参与者用公钥对发送信息进行加密，不需要安全秘密信道传送信息，减少了实际应用中代价，提高了协议安全性和传送系统的利用率。

(2)引入求离散对数的困难性假设，提高了协议执行中数据传输安全性。

(3)引入加密算法，能够抵御一些攻击者的攻击，保证数据信息顺利传递;

(4)引入验证算法，可以防止参与者和攻击者发布虚假信息，同时可以验证数据信息的有效性，提高了该多方可信计算协议的有效性。

(5)用随机多项式产生秘密份额，不但增强了秘密份额的有效性，而且增强了方矩阵秘密份额的安全性、可靠性。

但是该协议还有许多不完善之处，有待改进和提高:

(1)该协议仍然要求参与者是诚实或半诚实的，如果参与者是很恶意的，则该协议就会被破坏，而失去作用;

(2)加密算法性能，还有待于进一步提高和改进，使其能适应各种情况;

(3)验证算法，随着p增加，验证次数增加，这无疑给参与者带来计算负担，同时也带来了效率不高的问题。

［1］Yao A.Protocol for secure compulation［C］.//Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computers Science，Los Angeles，1982:159－164

［2］贾恒越，刘焕平.求矩阵逆的安全双方计算协议［J］.计算机工程与应用，2008，44(33):112－114

［3］Naor M，Pinkas B.Distributed Oblivious Transfer［A］.Advances in Cryptology:Asiacry’00 Proceedings:LNCS1976，Springer－Verlag，2000:200－219

［4］Cachin C，Micali S，Stadler M.Computationally private information retrieval with polyogarithmic communication［M］.Advances in cryptology，1998:308－319

［5］Luo Wen－jun，Li Xiang.A study of secure multi－party statistical analysis［C］.//Proceedings of IEEE International Conference on Computer Networks and Mobile Computing，Shanghai，2003:376－383

［6］Li Shun－dong，Dai Yi－qi.Secure two－party computationalgeometry［J］.Journal of Computer Science and Technology，2005，20(2):257－264

［7］Du Wenliang，Atallah M.J.Privacy－preserving cooperative scientific computation［C］.//Proceedings of the 14th IEEE Computer Security Foundations Workshop，Nova Scotia，Canada，2001:273－283

［8］王永兵，卢晓杰，张建中.一种基于身份的代理聚合签名方案［J］.济南大学学报(自然科学版)，2011，25(3):301－304

［9］罗文俊，李 祥.矩阵特征值的两方安全保密计算［J］.吉首大学学报(自然科学版)，2003，24(4):31－34

［10］Du Wenliang.A study of several specific secure two－party computation problems［D］.USA:Purdue University，2001:270－280

［11］罗文俊，李 祥.多方安全矩阵乘积协议及应用［J］.计算机学报，2005，28(7):1230－1236

［12］王小妹.安全多方计算的协议研究［D］.北京:北京邮电大学，2008:33－35