基于剖面数值模拟的地下水流系统结构控制因素——以鄂尔多斯白垩系盆地北部典型剖面为例

张 俊,侯光才,赵振宏,尹立河,王 冬

(西安地质矿产研究所,陕西西安 710054)

1963年,Toth[1]基于理想的二维均质各向同性小型泄水盆地模型,利用解析解绘制了理论上的地下水流系统流网结构,发展了地下水流系统理论,使水文地质的研究视野拓展到了区域(流域或盆地)尺度,研究对象转入到了以整个水系统与自然环境系统和社会经济系统间相互关系为着眼点的生态环境巨系统下的区域地下水系统[2-5]。

地下水流系统结构的研究是地下水系统研究的重要内容,也是正确评价和合理开发利用区域地下水资源的基础。流网分析是研究水流系统的有力工具,受限于当时的技术条件,Toth基于小型泄水盆地模型的流网分析采用解析法求解,涉及计算较复杂,且数学公式难以描述地下水运动复杂的交换条件和赋存条件,尤其是当含水层介质不是均质各向同性时,解析法计算难度更大,Toth对于复杂地形条件和非均质各向异性含水层对水流系统的影响只做了定性讨论。随后,Freeze等[6]用数值法绘制流网,讨论了任意地形和非均质各向异性介质对水流系统的影响,其中,非均质性仅分析了2种不同渗透系数含水层简单分层的情况,各向异性仅分析了简单地形条件下的情况,对复杂地形条件下形成的多层分级嵌套结构的水流系统未作详细分析。

Groundwater modelling system(GMS)软件作为地下水模拟专业软件,采用图形化界面,建模过程简单方便,图形表达功能强大。借助GMS软件建立剖面二维水流数值模型,自动生成剖面流网,通过自由改变模型的边界条件和含水层结构或参数观察流网的变化,可以帮助研究者方便直观地分析影响水流系统结构的各种因素,深化对水流系统的认识[7-9]。因此,本文采用GMS软件建立水流系统剖面二维数值模型,通过GMS软件自动生成的剖面流网图进行流网分析,并以鄂尔多斯白垩系盆地北部典型剖面水流系统(以下简称Ordos水流系统)为例,对比其与Toth水流系统结构上的差异,分析讨论边界条件以及含水层结构对水流系统结构的控制影响。

1 剖面二维水流系统分析

1.1 剖面二维数值模型

在GMS软件中利用栅格法生成剖面网格,上边界为定水头边界,假设初始水头和地形高程一致;垂向和底部为隔水边界。含水层概化为均质各向同性和均质各向异性介质,各向异性由水平渗透系数和垂向渗透系数的比值Kh/Kv表现,将模型概化为剖面二维稳定流模型。数值模型采用有限差分模型,采用GMS软件中的MODFLOW模块模拟获得剖面水头分布,流线由MODPATH模块通过添加示踪粒子自动生成。不同模型的边界条件和含水层参数通过在GMS软件中设置剖分单元格的属性来改变。

1.2 水流系统分析

水流系统的结构受边界条件和含水层结构两个方面的因素共同影响,其中,边界条件包括含水层厚度、盆地谷翼平均坡度、地形起伏度等条件;含水层结构主要包括含水层的非均质性、各向异性等条件。下面基于剖面二维数值模型生成的流网分析各个影响因素的控制作用。

1.2.1含水层厚度

含水层厚度主要影响区域水流系统。如图1所示,随着含水层厚度的增加,水流运动的空间增大,通过区域系统的水流开始出现,并逐渐增多。从图1(d)可看出,当含水层厚度足够大,至水势差影响可以忽略时,水流系统存在极限循环深度。

图1 不同含水层厚度水流系统剖面流网

1.2.2盆地谷翼平均坡度

盆地谷翼平均坡度对区域系统和局域系统均有影响。如图2所示,随着谷翼坡度增大,水势差增大,这导致从补给区向谷底的横向流动,即区域流增强,区域流动系统的范围增大,而局域流动系统的范围有所减小。

图2 不同盆地谷翼平均坡度水流系统剖面流网

1.2.3地形起伏度

如图3所示,地形起伏度主要影响局域系统,地形起伏的增大会增大局域系统的水势差,倾向于使局域流动系统的范围加大,区域流动系统没有明显变化。

图3 不同地形起伏度水流系统剖面流网

1.2.4含水层非均质性

如图4所示,均质各向同性介质中,含水层渗透系数K值大小的整体变化对水流系统结构无影响。水流系统结构主要受地形(边界条件)的控制,地下水从分水岭获得补给向排泄基准面汇流。局域分水岭和排泄点控制局域水流系统;区域分水岭和排泄点控制区域水流系统。

图4 均质各向同性介质不同K值水流系统剖面流网

对于非均质的情况,侯光才等[10]在研究鄂尔多斯盆地白垩系水流系统时,采用两种方法刻画了典型剖面(剖面基本概况见下文)含水层渗透系数的非均质性(图5(a)(c))。一种是按照传统的参数分区方式,分区的依据是平面上各含水组岩性并参考岩相做出的渗透系数分区;另一种是根据物探及抽水试验资料等,运用随机模拟方法建立了鄂尔多斯白垩系渗透结构。对比两种情况下的水流系统流网(图5(b)(d))发现,采用参数分区和随机模拟的流网结构差别不大,补给区和排泄区的分布位置基本一致,图5(b)在局部地段受非均质的影响,出现流线折射的现象,图5(d)中更为明显。但从整体来看,渗透系数的非均质性并没有改变各级循环系统的发育范围和规模。

1.2.5含水层各向异性

在数值模型中,含水层各向异性以含水层水平渗透系数和垂向渗透系数的比值Kh/Kv表示。如图6所示,均质各向异性介质中,Kh/Kv增大使垂向流动受抑制,水平流动占据优势,Kh/Kv对各级水流系统的循环深度具有明显的控制作用。Kh/Kv主要影响垂向流比例较多的补给区,它使补给区垂向流快速转为水平流,通过控制补给区下渗流的深度来影响整个水流系统的循环深度。

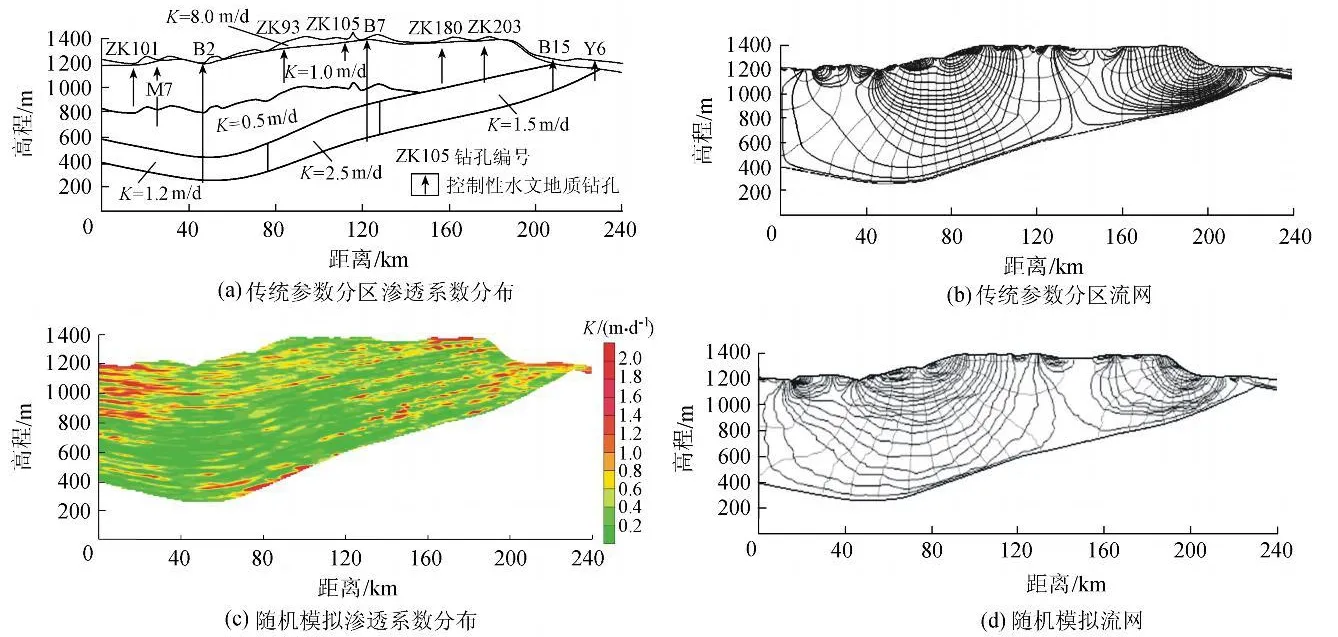
图5 不同渗透系数分布及水流系统剖面流网

图6 各向异性介质中不同Kh/Kv的水流系统剖面流网

2 Ordos水流系统分析

2.1 研究区概况

鄂尔多斯白垩系自流盆地是我国面积最大、结构最完整、具有典型意义的地下水系统[11]。盆地北部白垩系含水层厚度大,且无区域性稳定隔水层,各层地下水力联系密切,构成一个具有统一水力联系的巨厚含水体。盆地北部为沙漠高原,地表入渗条件好,降水入渗均匀,地下水面起伏与地形起伏一致,地势较高的梁地形成规模大小不等的地下水分水岭,地势低洼带分布众多湖(淖),成为地表水和地下水的汇流排泄点[12]。含水体内地下水流可穿层流动,形成了分级嵌套的多层结构流动模式,与托斯基于理论假设和数学推演得出的地下水流动模式相一致,为地下水流系统的研究提供了优良的场地,对于地下水流系统实例研究的开展具有重要的价值。

典型剖面西起宁夏平罗县东,经内蒙古鄂托克旗、乌审旗,东至陕西榆林市西,长约232km,剖面走向与地下水流向相同,横跨都思兔河和无定河两个地下水系统。剖面高程1200～1450m,由中部东胜梁分水岭向盆地两侧降低。

2.2 对比分析

Toth[1]假设的小型泄水盆地含水层为均质各向同性介质,而鄂尔多斯盆地白垩系含水层结构特殊,受其控制,流动系统也有其自身特有的结构特点。根据8个钻孔地下水分层水头分布、数值模拟、同位素及水化学示踪分析,综合确定了典型剖面不同循环系统地下水循环深度。Toth水流系统与Ordos水流系统结构特征对比见表1。

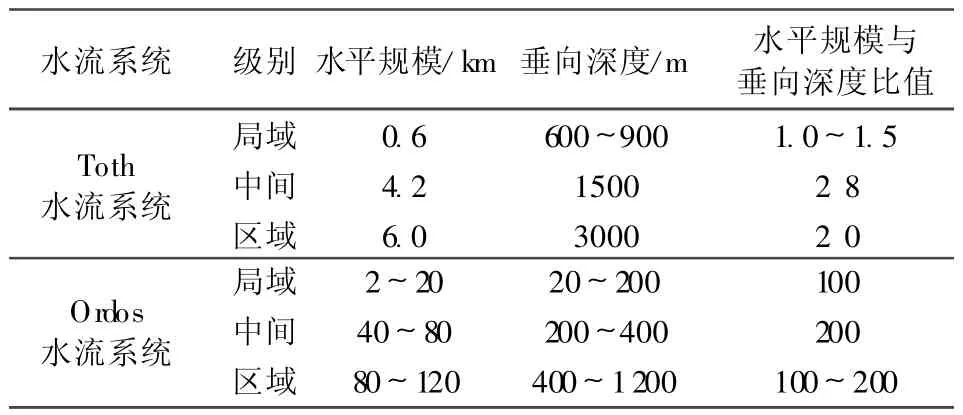
表1 Toth水流系统与Ordos水流系统结构特征

Toth水流系统假设的盆地宽度约为6000m,含水层厚度约为3000m。受盆地宽度和深度的限制,区域水流系统沿盆地边界流动,系统水平规模与垂向深度的比值为2;局域水流系统的水平规模受局域分水岭到排泄基准面水平距离的控制,范围600m,垂向深度受地形起伏度(即局域分水岭到排泄基准面平均坡度)控制,范围600～900m,局域系统水平规模与垂向深度的比值为0.67～1.0,而Ordos各级水流系统的水平发育规模,同样受各级分水岭和排泄基准面水平距离的控制,但垂向发育深度明显偏小,各级系统水平规模与垂向深度的比值达100～200。

根据前述分析,将含水层概化为均质介质对水流系统的流场结构影响不大,而数值模拟时,据各级水流系统循环深度反演计算得出的各向异性指标Kh/Kv值达1000～2000。Ordos水流系统典型剖面数值模型模拟了不同Kh/Kv下的水流系统结构,如图7所示,各向异性比对驻点(图中SP1,SP2)深度的影响很大,Kh/Kv为 2 000时的深度明显小于Kh/Kv为700时的深度。Kh/Kv值的增大是造成水流系统垂向发育深度显著变小的主要原因。

图7 典型剖面的流动系统结构示意图

Ordos水流系统典型剖面长度为240km,用地下水分层水头反算出的Kh/Kv在1000左右。在鄂尔多斯白垩系盆地各水源地数值模拟研究中,各水源地剖面长度在30km左右,而根据水流循环深度反算出的Kh/Kv在10～100之间。对比不同尺度的水流模型发现[13],Kh/Kv大小对模型剖分单元格尺寸有依赖,即随着模型尺度的增大,模型剖分单元格尺寸相应增大,Kh/Kv也将增大,Kh/Kv具有一定的尺度效应。究其原因,主要与含水层的结构有关。鄂尔多斯盆地北部白垩系含水层主要为河湖相层状沉积,泥岩透镜体及弱透水层呈水平层状发育。在水平方向,水流优先从高渗透区通过,这些高渗透区相互连通,形成水流优先通过的网络。在这个网络中,水流沿最小阻力路径流动,使模型单元格的水平向等效Kh值比简单的算术平均值要大,这使Kh随模型剖分单元格尺寸的增大有增大的趋势。在垂直方向,水流受到众多泥岩透镜体的影响,由于这些泥岩透镜体均为水平层状分布,其对垂向水流的阻碍具有叠加效应。因此,随着模型尺度的增大,模型单元格的垂向等效Kv值比算术平均值要小得多,这使Kv随剖分单元格尺寸的增大而显著衰减。因此,随着模型剖分单元格尺寸的增大,Kh增大而Kv衰减,Kh/Kv显著增大。

3 结 论

a.流网分析是水流系统研究的有力工具,通过GMS建立剖面二维水流数值模型,操作方便,形象直观,能很好地用来进行水流系统结构分析。

b.水流系统的结构受边界条件(含水层厚度、盆地谷翼平均坡度、地形起伏度)和含水层结构(非均质性、各向异性)影响,其水平发育规模主要受地形控制,而垂向循环深度主要受控于含水层水平渗透系数和垂向渗透系数的比值Kh/Kv。

c.Ordos水流系统与Toth水流系统模型类似,具有多层分级嵌套的循环模式,但前者受白垩系含水层层状沉积结构的控制,水流系统水平和垂向范围差异巨大。

d.数值模型中采用的Kh/Kv值与含水层结构有关,并且依赖于模型剖分单元格尺寸的变化,具有一定的尺度效应,即随着模型尺度的增大,Kh增大而Kv衰减,使大尺度模型中Kh/Kv显著增大。

[1]TOTH J.A theoretical analysis of groundwater flow in small drainage basin[J].Journal of Geophysical Research,1963,67(11):4375-4387.

[2]张人权,梁杏,靳孟贵,等.水文地质学基础[M].6版.北京:地质出版社,2011:86-88.

[3]姬亚东,柴学周,刘其声,等.大区域地下水流数值模拟研究现状及存在问题[J].煤田地质与勘探,2009,37(5):32-36.

[4]鲁程鹏,束龙仓,刘丽红,等.基于灵敏度分析的地下水数值模拟精度适应性评价[J].河海大学学报:自然科学版,2010,38(1):26-30.

[5]张人权,梁杏,靳孟贵,等.当代水文地质学发展趋势与对策[J].水文地质工程地质,2005,32(1):51-56.

[6]FREEZE R A,WITHERSPOON P A.Theoretical analysis of regional groundwater flow:2.effect of water table configuration and subsurface permeability variation[J].Water Resources Research,1967,3(2):623-634.

[7]郝治福,康绍忠.地下水系统数值模拟的研究现状和发展趋势[J].水利水电科技进展,2006,26(1):77-81.

[8]束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析[J].河海大学学报:自然科学版,2007,35(5):491-495.

[9]王丽霞,刘芳,唐泽军.基于GMS的石羊河流域含水层空间结构变化的可视化研究[J].干旱区地理,2011,34(1):62-69.

[10]侯光才,张茂省.鄂尔多斯盆地地下水勘查研究[M].北京:地质出版社,2008:255-259.

[11]陈梦熊,马凤山.中国地下水资源与环境[M].北京:地震出版社,2002:385-390.

[12]侯光才,林学钰,苏小四,等.鄂尔多斯白垩系盆地地下水系统研究[J].吉林大学学报:地球科学版,2006,36(3):391-398.

[13]FLECKENSTEIN J H,FOGG G E.Efficient upscaling of hydraulic conductivity in heterogeneous alluvial aquifers[J].Hydrogeology Journal,2008,16:1239-1250.