PID参数继电反馈整定法的改进

高峰

（商丘师范学院 物理与电气信息学院，河南 商丘 476000）

文中首先分析了PID参数继电整定法的基本原理和操作过程，给出了Astrom法的自整定公式和PM法的自整定公式。然后又在此基础上提出了一种改进的继电整定方法，并推导了相应的整定公式。最后，通过实际仿真对比，证明了利用改进的方法进行PID参数整定可以获得更好的控制性能。

1 继电反馈整定法的基本原理

PID参数的继电整定方法是由瑞典著名学者Astrom和Hagglund两人共同提出的[1-3]，其原理框图如图1所示。其中继电器环节采用带滞环的继电器，它有滞环宽度ε和滞环幅d值2个参数，开关K用于选择继电测试或者PID控制器调节。

具体的参数整定步骤如下：

1）通过人工调节使系统进入稳态。

2）按下整定按钮，使开关K与点M接通；选取合适的ε和d使系统获得等幅振荡的周期运动。

3）根据产生的等幅振荡计算对象的临界振荡εC频率及临界振荡增益KC。

4）通过整定公式计算PID控制器的参数。

5）自动调整PID参数。

党的十八届三中全会进一步明确提出，公有制经济和非公有制经济都是社会主义市场经济的重要组成部分，都是我国经济社会发展的重要基础。

6）开关K接通N点，实行PID控制。

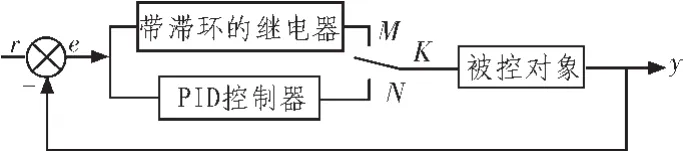
图1 继电反馈整定法的原理图Fig.1 Principal diagram of relay feedback tuming method

在获取临界信息后，通常采用Astrom法和PM法的整定公式获得PID参数。

Astrom法的整定公式如下：

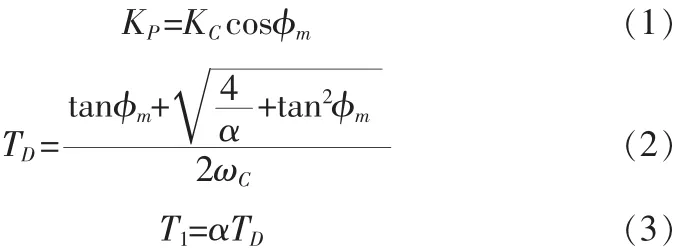
PM法的整定公式如下：

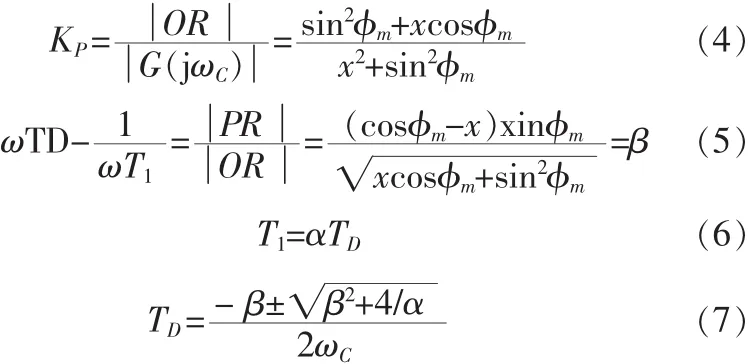
其中α通常取4。利用上面两种方法整定得到的参数一般比较粗糙，控制效果较差。

2 继电反馈整定法的改进

为了得到更加优化的PID参数，可以对前述的继电实验加以改进，在继电环节和被控对象之间设置一个积分器。在这种情况下进行实验，被控对象在高频只需至少-的相位滞后，就可以得到等幅振荡的周期运动。其频率就是虚轴的负半轴与幅相频率特性曲线的交点的频率。此外，积分器的设置能够促进高频信号的衰减，使谐波中的高频成分大大减少，基波成分所占比例得到提高，从而改善了描述函数的精度[4-6]。含积分器的继电整定原理如图2所示。

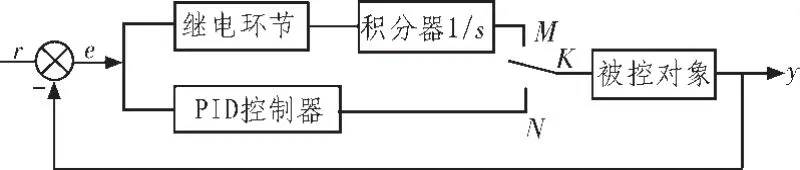
图2 改进的继电整定法原理图Fig.2 Principal diagram of improved relay feedback tuming method

设开环幅相频率特性曲线与虚轴的负半轴相交于点B，该点的频率即为临界振荡频率ωb。

T可以通过实验测得。同样可得到被控对象在这个频率点的幅值近似为

A即为被控对象的输出y的振荡幅值，亦是通过实验测得。并且由式（9）可知，通过选择合适的继电环节的幅值d能够对A进行限制，以保证系统正常工作。确定ωb和Kb之后，便可以进行PID参数整定。PID控制器作用下的被控对象幅相频率特性曲线如图3所示。

图3 PID控制器作用下的幅相频率特性曲线Fig.3 Magnitude-phase characteristics curve under PID control

通过选择不同的KP，TI，TD值能够使幅相频率特性曲线上的点随意地移动。图3中，选择不同的KP值，会使点C沿径向移动，而选择不同的TI和TD值能够使点C沿幅相频率特性曲线的切向移动。点C能够发生移动的角度区间为（-90°，90°）。现欲将点 C移至同时满足相位裕度φm和幅值裕度Am的点上，可以得到

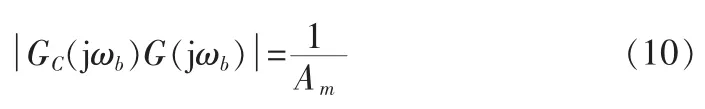
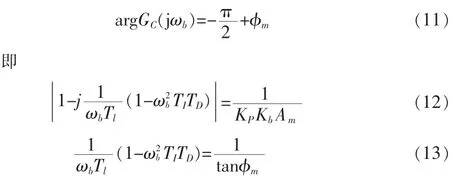
根据经验，令TI和TD满足

α通常取4，最后解得

式（14），（15）和（16）即为改进后的 PID 参数整定公式。

3 仿真实验

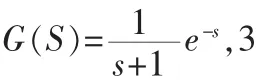
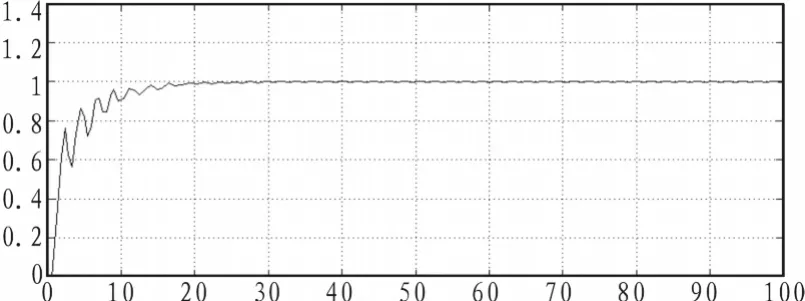
图4 基于Astrom法的系统单位阶跃响应曲线Fig.4 Unit step response curve of the system based on Astrom method

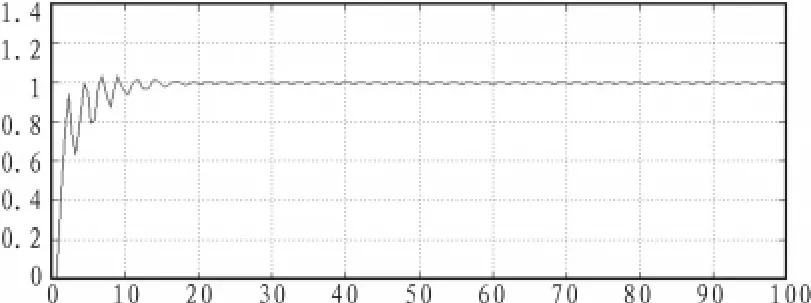
图5 基于PM法的系统单位阶跃响应曲线Fig.5 Unit step response curve of the system based on PM method

4 结束语

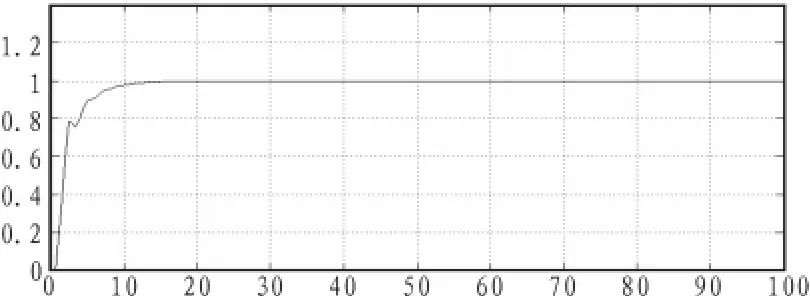
图6 基于改进方法的系统单位阶跃响应曲线Fig.6 Unit step response curve of the system based on improved method

由对象的仿真可以看出，基于Astrom法整定出的参数的系统单位阶跃响应曲线在20 s开始稳定；而基于PM法整定出的参数的系统单位阶跃响应曲线也在20 s开始稳定；基于改进方法整定出的参数的系统单位阶跃响应曲线在15 s开始稳定。而且前两者的曲线比后者的震荡要明显的多。所以得出结论：由改进后的方法得到的PID参数实行控制，系统性能明显优于Astrom法和PM法。

[1]Astrom K J，Hagglund T.Automatic tuning of PID controller[J].Research Triangle Park， Instrument Society of American，1988，5：123-128.

[2]Astrom K J ，Hagglund T.PID controls：theory，design and tuning[J].Research Triangle Park，Instrument Society of American，1995，34（7）：46-52.

[3]Ziegler J G，Nichols N B.Optimum settings for automatic controllers[J].IEEE Trans on ASME，1942，65：759-768.

[4]Vandecursen J M，PePerstrate J A.Internal model control with improved disturbance rejection[J].Int，J control，1995，62（4）：983-999.

[5]Tan K K，Lee T H，Wang Q G.An enhanced automatic tuning procedure for PI/PID controllers for process control[J].AICHE Journal，1996，42（9）：2555-2562.

[6]Wendell S R.Takecontrol of PID tuning[J].Plant Engineering，2005，59（9）：57-60.