大型平面有轨对拉式弧形闸门流激振动特性及抗振措施

辛华荣，王 建，严根华，赵建平

(1.江苏省水利工程建设局，江苏 南京 210029;2.南京水利科学研究院，江苏 南京 210029)

对于平原水系河道开阔、航运繁忙的地段，修建挡水闸门需要综合考虑和妥善处理防洪与通航两者的关系.某防洪控制工程闸门采用平面有轨弧形双开门结构较好解决了这2个问题，取得满意效果.该水闸孔口净宽90.0 m，弧面半径60.0 m，弧形门外侧面板总弧长58.325 m，门高7.5 m;支臂采用3根Φ520 mm×18 mm钢管组成的桁架构杆.弧门支铰采用Φ600 mm球关节轴承.根据该工程闸门启闭的特点，平面弧门启闭采用固定卷扬式启闭机.启闭机的启闭容量为600 kN，钢丝绳直径58 mm.启闭机运行速度为1 m/min，绳长约196 m，运行绳长约50 m.闸门绕支铰由门库转至挡水位置约需60 min.水闸总体布置和闸门结构布置见图1和图2.

图1 水闸总体布置Fig.1 Layout of the sluice

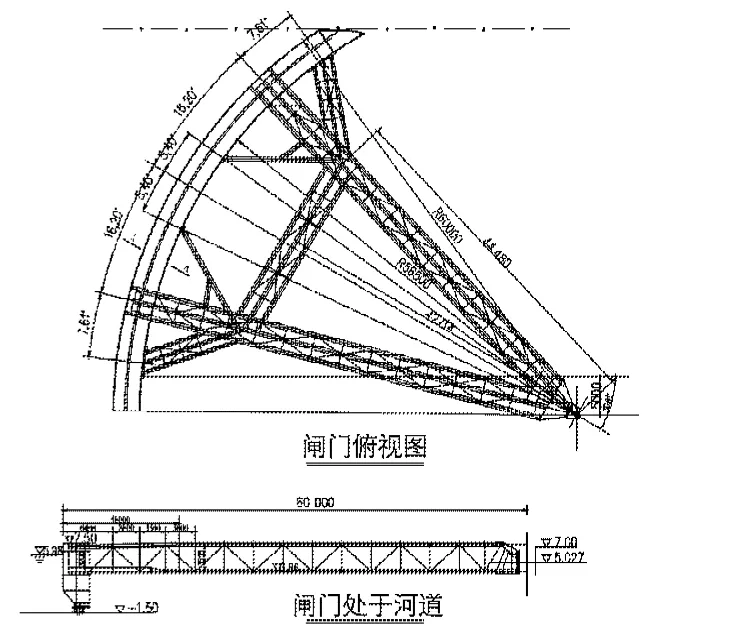
图2 闸门结构布置(单边)(单位:高程:m，长度:mm)Fig.2 Arrangement of the gate structure(height:m，length:mm)

1 水动力荷载特性

水闸结构运行过程中将发生振动，其主要原因在于水动力荷载与结构固有特性产生不利组合作用［1－2］所致.因此预测和控制闸门振动需要对作用于闸门结构的水动力荷载进行认真研究，为结构的振动分析提供基本依据.

1.1 流态观测

闸门开启或关闭过程中水流运动属于缺口溢流，出流在横向形成一定扩散，并在河道两侧形成回流至闸门附近，回流范围随开度增大而逐渐明显，对下游影响范围更长、更宽.水流在通过闸门口门时，由于此时侧缘断面存在折角，水流收缩并汇中，在经过止水时出现二次收缩聚中，水流被缩窄在止水后横向扩散并形成交汇波浪，主流上部直接落到下游.总体上看，在止水处形成的侧收缩对流态影响较大.上游来流基本平稳，闸门在箱体充水、轨道压重100 t状态下能平稳运行.当闸门内液位降低而发生振动时，闸门箱体及支臂在水体中上下方向发生振动对上下游流态造成极大影响，导致水面波动加剧，而水面波动又反作用到闸门门体.这种流场与结构的相互作用更进一步加剧了闸门振动.闸门局部开启时典型水流流态见图3.

图3 闸门局部开启时典型水流流态Fig.3 Flow pattern with gate opening

1.2 水流脉动压力分布特性

为了较完整地掌握闸门的脉动压力分布数据，在闸门面板、门后、支臂等部位布置了5个水流脉动压力测点，其中1～4号点位于上游侧，5号点位于下游侧(见图3).试验测量了不同运行工况下作用于闸门的脉动压力数字特征及其谱特征，明确了脉动压力的量级及其脉动能量在频域的分布规律.

当上游水位为5.98 m，下游水位为4.70 m时，作用于闸门上游面脉动压力均方根值随测点位置向河岸侧减小;同一测点随着闸门开度的增大，脉动压力均方根值逐渐加大(见图4).较大脉动压力值出现在闸门开度n0=4 m时的P1测点，均方根值为0.091 m水柱，占总水头的7.11%.说明随着闸门开度的加大、下泄流量的增加，水流扰动力随之加大(图5).若定义C1为脉动压力系数为水流脉动均方根值;u为泄流口部位来流平均流速)，则闸门在端点部位的脉动压力系数约为 0.1.

水流脉动压力的谱特征主要反映作用于闸门结构各部位脉动压力在频域的能量分布情况.图6绘出了典型工况下(上游水位5.98 m，下游水位4.7 m，工作门开度1 m)作用于门体的脉动压力时域过程、概率密度及功率谱密度曲线.由图示曲线可见:大部分时域过程线具有正态分布的各态平稳随机过程特征，即主要脉动能量一般集中在1.0 Hz以内的低频区.

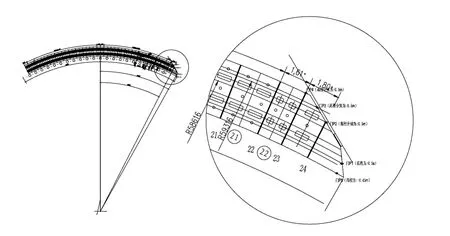
图4 脉动压力测点布置简图Fig.4 Arrangement of measuring points

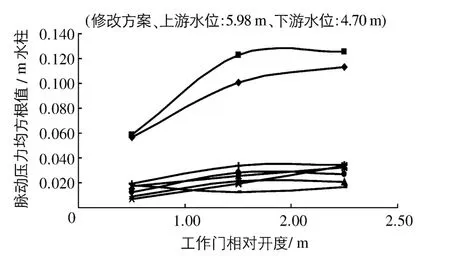
图5 闸门脉动压力随开度变化关系Fig.5 Relation between pulsating pressure and gate opening

图6 典型测点闸门脉动压力时域过程、功率谱密度、概率密度Fig.6 Lines of pulsating pressure，power spectral density and probability density

根据水流脉动压力测试结果，水闸运行过程中作用于闸门体的水流脉动压力具有如下特征:靠近河中央端部的脉动压力达到最大，沿门宽方向逐渐减少.脉动压力在频域的能量分布具有低频特征，一般主能量分布在0～1 Hz的频率范围内.这是诱发闸门产生强烈振动的基本振源［3－4］.

2 闸门结构的动力特性

闸门结构的运动可用如下微分方程表

式中:M，C，K分别为质量矩阵、阻尼矩阵、刚度矩阵;δ为结点位移;P(t)为动力荷载.当闸门在运行过程中发生振动时，流体与结构将产生耦合作用，结构的振动特性将产生变化.这是因为闸门的振动必然引起水体压力的波动，水体压力波动又会影响闸门的振动，这是一个典型的液体和弹性体的耦合振动问题.经推导可得到如下方程:

式中:Mp=SDT就是通常所称的附加质量阵.求解上述方程就可获得结构的动力特性参数.

根据闸门结构的支承特点和实际工况，对支铰约束、上下游水压力作用及闸门箱体内有水情况下的振动模态特性进行分析.其中上游水位5.89 m，下游水位4.30 m，箱体内水体水位4.30 m.图7为各阶振动模态.由图可见，在此条件下，闸门结构1阶振动模态频率为0.161 Hz，门叶上下抖动;2阶模态频率为0.203 Hz，闸门整体切向转动变形;3阶模态频率为0.241 Hz，闸门整体扭转振动变形;4阶模态频率为2.600 Hz，闸门支臂的弯曲变形振动;4阶以上模态均反映闸门支臂的对称、反对称弯曲变形振动;支臂与面板的组合1阶弯曲振动频率为4.72 Hz.

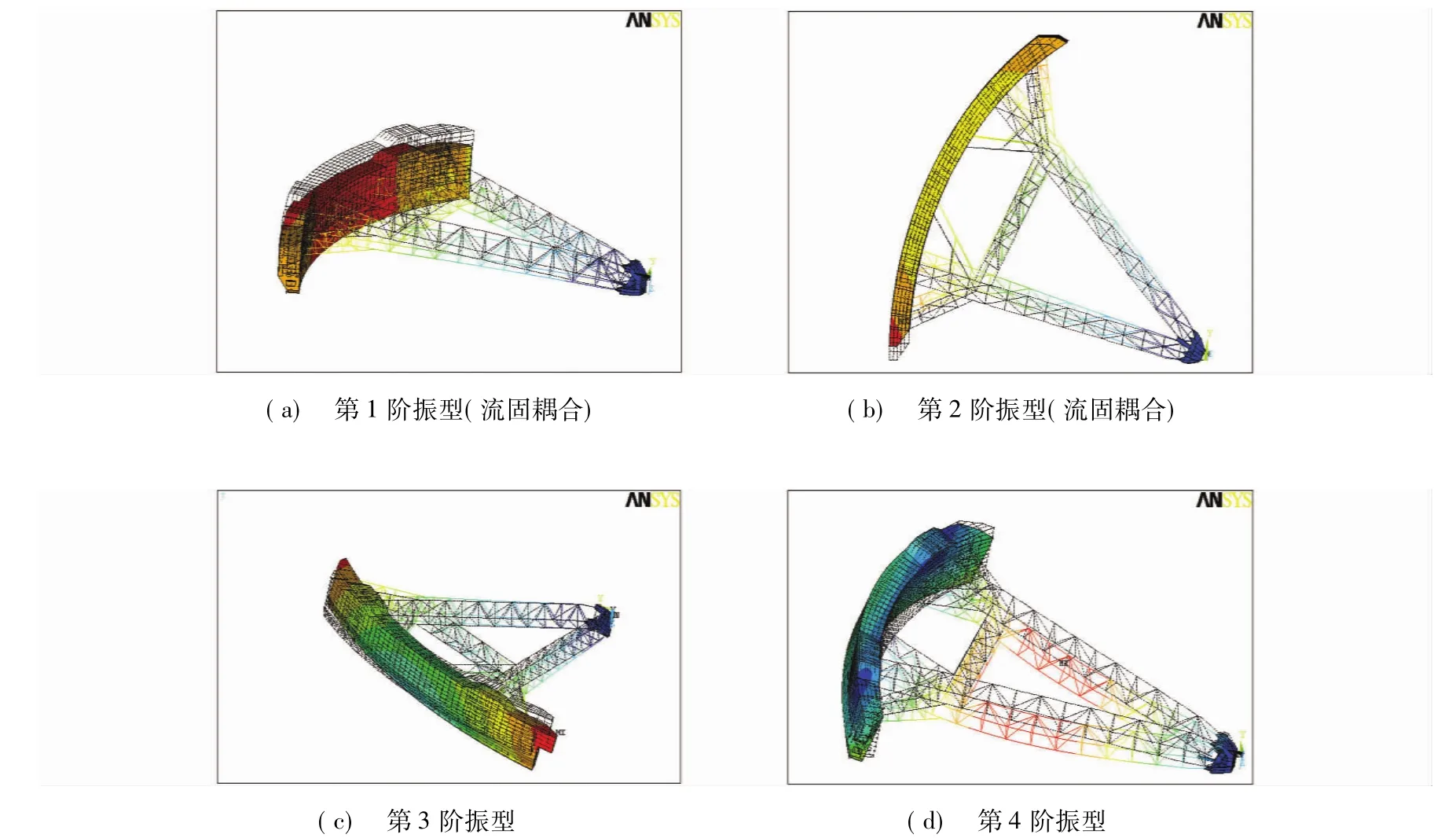
图7 各阶振动模态Fig.7 Vibration mode pattern of the gate

3 对拉式闸门的流激振动特性

3.1 模型设计和测点布置

由于该闸门结构特殊，运行方式与常规闸门有较大区别，除常规匀速启闭外，还有门缝输水要求，且在特殊情况下需要进行浮运，下游流态复杂，需要关注的起控制性作用的水力学参数较多.首先要关注对闸门受力起主要作用的上下游水位及流量，其次在闸门上下游水位确定时需要控制对应的闸门开度及门内液位这两个基本参数.因此在多组变化的水力学参数下，闸门运行过程中可能出现的不利振动问题需要高度重视.

从本质上讲，闸门流激振动属于水弹性振动范畴，动水作用下的运动符合如下动力方程［5］:

式中:¨D，˙D，D分别表示结点的加速度向量、速度向量和位移向量;F表示作用在水－固接触界面结点上的动水压力向量，一般包括闸门静止时作用在闸门上的水流脉动压力向量F1和闸门振动引起的扰动流场作用在流固界面上的附加荷载F2.

根据上述结构运动方程，考虑到振动试验一般在水介质中进行，因此闸门的水弹性模型应当同时满足几何尺寸、质量密度、阻尼、弹性模量、水流动力等参数的相似性.根据相似原理，经推导可得如下闸门结构各参数的比尺要求:几何比尺Lr=20，质量密度比尺ρr=1，弹性模量比尺Er=Lr，泊松比比尺μr=1，阻尼比尺Cr或者临界阻尼比尺ξr=1.显然，目前市场上没有同时满足上述参数的型材，需要专门制作模具，本次试验采用重金属粉、高分子材料等进行多组分特种材料研制，并对研制材料进行测试.测试结果表明:选用的水弹性材料的特性基本达到材料密度ρm=ρp、结构弹模比尺Er=Lr的要求，即满足弹性模量和密度需要满足的条件:CE/CgCρ=Cl(其中CE为弹性模量相似常数，Cg为重力相似常数，Cρ为密度相似常数，Cl为几何形状相似常数，其中Cg=1).

本项试验的闸门门体及支臂结构采用完全水弹性模型进行制作，并展开动水作用下闸门流激振动特性研究.全水弹性模型既满足水动力学相似，也满足结构动力学相似及其流固耦合振动相似，能够较好地预报闸门结构的流激振动特性.

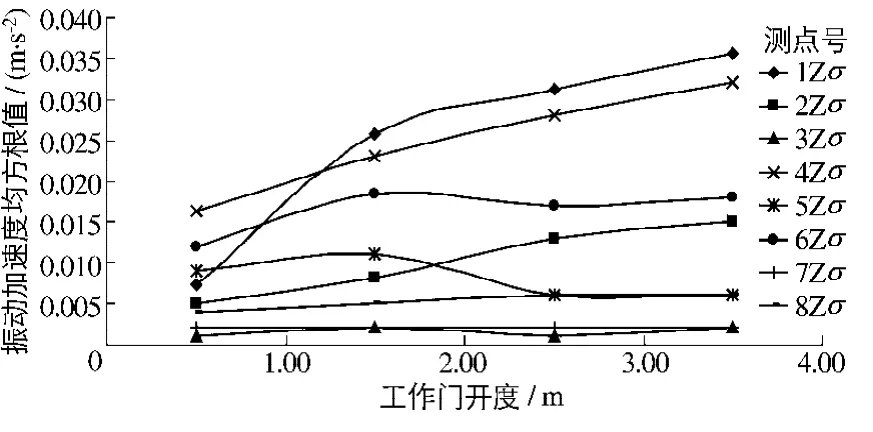
图8 工作门振动加速度随开度变化关系Fig.8 Relation between vibration acceleration and gate opening

3.2 闸门稳定状态下的结构振动特征

典型工况、各开度下的工作门振动加速度均方根值随开度的变化关系见图8.由数据可知，门体端部和中部的振动量较其他点略大，且随开度增大而略有增大，其中近端部1#点出现大值，最大振动加速度均方根值为0.036 m/s2.这是由于闸门局部开启过程中下泄水流的脉动荷载主要作用在紧靠河道侧的闸门端部，其振动能量的传递也由河中央侧门体向岸边侧结构传递及衰减的缘故.

3.3 闸门不稳定强振状态下的结构振动加速度

在取得闸门稳定运行时的振动加速度后，对闸门发生强烈振动情况下的振动加速度进行观测和测量.试验时首先将门叶箱体内进行充水，水位与下游基本持平后闸门开始泄流运行，随后通过水泵抽水逐渐降低门内水位，察看闸门振动情况.观察结果显示，在上游水位5.98 m，下游水位4.7 m和4.3 m等不同水位工况下，门体箱内给定水位时，闸门局部开启时振动量级相对较弱，即闸门处于平稳运行状态.但随着门体箱内水位逐渐下降，闸门总重量逐渐减少，亦即作用于闸门轨道处垂向压力降低，在水流动荷载作用下容易诱发闸门结构的强烈振动.

当闸门轨道处的垂向压力下降到某一临界值时，闸门首先出现低频小幅度的上下方向振动，随着门内水体进一步略微减少时，闸门出现低频大幅度的振动［6－7］.此时闸门并不是完全悬浮在水里面振动，而是出现上下剧烈振动，浮起后又下压到活动轨道上，类似一把锤子，重重地冲击在活动轨道上后又浮起，循环上下运动.对闸门模型停止抽水，可见闸门仍然保持低频大幅度的振动，发生强烈振动时的振动加速度最大量级达到3～4 m/s2.由于门体尾部在门槽内，水动力作用减弱，使门体端部(河道侧)与尾部(门库侧)振动不在一个水平面内，形成闸门端部上翘或下跌状扭转振动.

图9和10分别为典型工况下的振动加速度时域过程和闸门发生强烈振动时振动加速度时频变化.

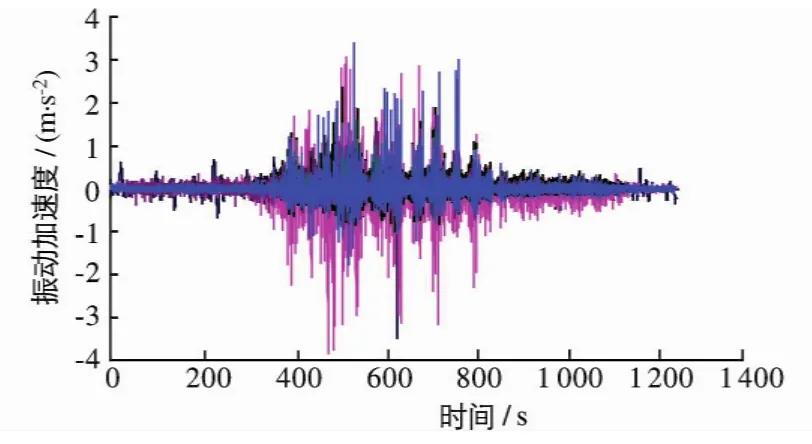
图9 典型闸门振动加速度时域过程Fig.9 Process of vibration acceleration

图10 闸门发生强烈振动时闸门振动加速度时频分析Fig.10 Time-frequency vibration acceleration

由图可见，闸门在泄流条件下，随门内水位的变化闸门结构出现平稳、逐渐起振、强烈振动、恢复平稳等过程.试验结果显示，闸门强烈振动的主能量主要集中在1.1～1.5 Hz范围内(模型值)，相应原型值约为0.246～0.336 Hz.门体产生强振时，闸门振幅随时间不断变化，起振时的振幅值与发生强振时的数值差别较大，从起振时的逐渐增大直到发生强振状态，其实际大小与当时水位、门内水位等关系密切.

分析试验结果，门体箱内水位与强振状态有如下规律:(1)上游水位5.98 m，下游水位4.70 m时，闸门出现强烈振动的门内水位为3.56～3.60 m;(2)上游水位5.98 m，下游水位4.30 m时，门内水位为3.22～3.24 m;(3)上游水位5.38 m，下游水位3.70 m 时，闸门出现强烈振动的门内水位为2.38～2.44 m;(4)上游水位5.38 m，下游水位4.30 m 时门内水位为2.88 ～2.96 m.

闸门结构原方案整体振动试验结果显示，该水闸在设计100 t压力(导轨处)条件下闸门启闭操作、局部开启泄流运行基本平稳;但随着箱内水位的下降，闸门出现强烈振动，振动出现的门内水位随上下游水位的变化而变化.一般门内水位在60 t左右时(水位为60 t)，闸门即出现强烈振动，在局部开启泄流时尤为突出.

试验结果表明，闸门出现大幅度振动时，振动的主能量主要集中在1.1～1.5 Hz(模型值)，相应原型值约为0.246～0.336 Hz，实际此时闸门结构出现了共振现象.这种大幅度振动，一方面对上下游水流造成较大影响，上下游水面波动加剧;另一方面，从振动响应来看，闸门自身在振动后，对金属结构部分如闸门结构、活动轨道必将造成严重破坏，威胁工程安全.因此，实际工程中必须避免出现这种振动状态.

4 结构振源分析与控振措施

4.1 结构振源分析

水流流态观测显示，随闸门开度增大或减小，水流在通过闸门口时，由于此时闸门端面(侧缘面)存在折角，水流收缩并汇中，在经过止水时，在止水处二次收缩聚中，水流被缩窄后流向下游时在止水后横向有所扩散并形成交汇波浪，主流上部直接落到下游.总体上看，在止水处形成的侧收缩对流态影响较大.

若降低闸门内水位而发生振动时，闸门门体及支臂在水体中上下方向发生振动对上下游流态造成极大影响，此时水面波动加剧，水面波动又反作用到闸门门体.这种流场与结构的相互作用更进一步加剧了闸门振动.

根据闸门泄流流态观测、水动力荷载、闸门流激振动测量、启闭力与箱内水位分析，以及闸门结构流固耦合振动特性分析等研究成果，得出目前闸门结构设计体型基本合适，闸门在给定工况下可以满足平稳运行要求，但尚存在如下问题:

(1)当门体箱内水位逐步降低时，闸门结构会发生强烈振动，其振动量足以损毁闸门结构，尤其是支臂及支铰结构.因此门体箱内的水位控制十分重要.

(2)闸门结构在泄流过程中下泄水流对底缘产生一定的扰动作用，导致诱发闸门结构的强烈振动.

(3)闸门支臂的若干低阶振型主要反映弯曲振动，频率低而且比较密集，抗扭刚度差，在强振状态下容易产生破坏.

(4)水流在通过闸门口门时，由于端面(侧缘面)存在折角，水流收缩并汇中，在经过止水时，在止水处二次收缩聚中，而后横向扩散并形成交汇波浪.总体上看，折线形侧收缩对流态影响较大.因此，可以考虑对闸门端部体型进行流线化修改.

因此，上述问题需要通过对结构和闸门运行方式的控制进行优化处理.

4.2 闸门结构优化及控振措施

根据上述存在问题，拟通过以下方式进行闸门结构优化:

(1)闸门底缘和端面体型的修改闸门底缘形式及端面体型是影响结构振动的重要因素之一.经设计修改，采用如下闸门端面体型(图11(a))，以平顺下泄水流流态.

(2)闸门支臂结构修改闸门结构的动力特性分析结果显示，该水闸闸门属于低刚度、长支臂结构，结构抗扭刚度弱，需要进行适当调整优化.根据结构振动模态特性，拟在支臂变形最大部位增设一道拉杆，修改布置见图11(b)，拉杆端面尺寸与第一道拉杆相同.

通过对原方案闸门结构的流态观测与闸门振动关系分析，闸门流激振动特征试验，门内水位与闸门振动的关系研究等，提出了闸门修改和优化方向，为确保平面弧形闸门的安全运行奠定了基础.

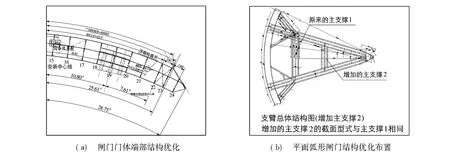
图11 闸门结构优化Fig.11 Optimization of gate structure

4.3 优化方案效果

优化结构的流激振动试验重点考查如下几个方面:(1)非浮运情况下，不同设计上、下游水位、闸门开度组合条件下，研究测定闸门门缝过流情况下(此时对应的水位不一定是门缝输水期的水位)即将发生起浮或强振时对应的门内水位，取得相同水位开度下不同门内水位对应的闸门振动加速度、位移及动应力等参数;(2)测定闸门稳定运行情况下门缝过流时的闸门振动加速度、动位移及动应力等，预报闸门处于稳定情况下的振动响应，明确振动类型、性质及其量级等;(3)测定闸门在不同上下游水位、闸门开度及门内水位组合条件下，闸门开门期、关门期动水启闭状态下闸门振动情况，考察闸门启闭过程中，由于支臂在水中运动对水流扰动、动态启闭过程是否发生不利流态，以免流固耦合作用造成振荡等;考察启闭过程中是否会由于启闭系统不稳定、上下游水位不稳定、门内水位变化等组合情况对闸门产生不利影响，是否需要控制门内水位等.

通过对优化方案闸门水弹性振动试验结果的分析，优化方案具有如下抗振效果:

(1)优化方案的起振水位低于原方案，亦即闸门的水动力条件比原方案好，门体受到的水动力荷载要小，抗振能力较为优越，说明在相同的门内水位条件下，优化方案的运行将更加平稳，尤其在下游高水位情况下更为突出.

(2)对闸门处于稳定运行状态下部分工况的闸门振动量而言，优化方案的振动最大值小于原方案.原方案振动量的平均值约为修改方案的1.3～2.5倍(见图12).从细部来看，优化方案闸门头部的振动量值也比原方案明显减小.因此，闸门结构的优化方案取得了良好的抗振效果.

图12 优化方案与原方案工作门振动量比较(上游水位:5.98 m，下游水位:4.70 m)Fig.12 Comparison of vibration amplitude between optimization and original gate's scheme

5 结语

大型对拉式有轨平面弧形闸门是一种新型大跨度门型，适合于需要防洪和通航要求的开阔河道.该闸门具有外表美观、安全可靠、操作运行方便等特点.由于闸门跨度大，结构刚度相对较弱，振动基频很低，这与水流脉动压力荷载的主能量常常重合，因此较小的水流扰动就有可能引发闸门强烈振动.本文根据水流运动和结构动力特征，提出了同时改善水流条件和增强支臂面板整体性的优化方案，并经过水弹性振动试验证明了修改方案的优越性，因而取得满意的优化效果.

［1］严根华.水工弧形闸门三维水弹耦合共振频率的数值计算［J］.水利水运科学研究，1993(1):13-19.(YAN Gen-hua.Study on resonance frequencies of hydraulic radial gate hydro-elastic vibration［J］.Journal of Nanjing Hydraulic Research Institute，1993(1):13-19.(in Chinese))

［2］严根华.水工弧形闸门振动分析及动力安全设计技术研究［J］.金属结构，1998(3):22-25.(YAN Gen-hua.Vibration analysis and study of dynamic safety design technology for hydraulic radial gate［J］.Metal Structure，1998(3):22-25.(in Chinese))

［3］YAN Gen-hua.Experiments and researchs on flow-induced vibration of large radial working gate in sand sluicing chamber［C］∥Proceedings of 16th IAHR-APD Congress and 3rd Symposium of IAHR-ISHS，2008.

［4］CHEN Fa-zhan，YAN Gen-hua，HU Qu-lie.Design of large span gate structure and study on anti-resonance measure［C］∥Proceedings International Symposium on Hydraulic Physical Modeling and Field Investigation，Beijing:China Waterpower Press，2011.

［5］刘士和.高速水流［M］.北京:科学出版社，2005.(LIU Shi-he.High velocity flow［M］.Beijing:Science Press，2005.(in Chinese))

［6］严根华.水工闸门流激振动及动态优化设计［J］.水利水运科学研究，1999(1):65-68.(YAN Gen-hua.Hydraulic gate flow-induced vibration and optimization design［J］.Journal of Nanjing Hydraulic Research Institute，1999(1):65-68.(in Chinese))

［7］严根华，赵建平.淹没水跃作用下大宽高比闸门的流激振动试验研究［J］.振动工程学报，2005，18(增刊):45-49.(YAN Gen-hua，ZHAO Jian-ping.Flow-induced vibration experiment study on the great width to the high scale gate under submerged jump［J］.Journal of Vibration Engineering，2005，18(Suppl):45-49.(in Chinese))