低空投弹仿真与测试技术

王绪军，田应元

(中国船舶重工集团公司公司第七一○研究所，湖北 宜昌 443003)

低空投弹仿真与测试技术

王绪军，田应元

(中国船舶重工集团公司公司第七一○研究所，湖北 宜昌 443003)

空投型武器弹药是当今先进武器发展的重要组成部分，如航空炸弹、钻地弹、鱼(水)雷、深水炸弹等。其中一部分采用低空投放，投弹精度和空中弹道的稳定性直接影响武器系统的正常使用和攻击效能。本文建立了低空投放条件下的弹伞弹道理论模型，通过数值仿真与试验测试进行对比研究，为武器系统参数的确定及射表的编拟打下基础，同时对指导飞机投弹有着十分重要的意义。

投弹;仿真;测试

0 引言

航空弹药战术技术性能不断提高以及作战的需要，对投弹的精度要求以及空中弹道稳定性要求越来越高。精确制导弹药相对于普通弹药其作战效能有了大幅提高，但同时精确制导弹药的抗冲击过载能力随着各种精密仪器的增多在不断降低，并对空投弹道参数如弹体落速、弹体姿态、落点散布以及留空时间等均有着严格的要求。空中弹道尤其是带减速伞的弹伞系统的空中运动十分复杂。弹道仿真为弹药研制初期的系统参数设计及空投试验提供理论指导，同时，弹道试验测试为理论弹道的修正提供依据，并为射表的编拟奠定基础。因此，弹道的仿真和测试研究对航空弹药的研制及有效使用都有着十分重要的意义。

1 弹道建模与仿真

航空弹药投放通常分为带伞和不带伞2种状态。对于无伞弹药，弹体的气动外形及衡重参数决定了空中弹道的稳定性，无动力弹道模型参照文献［1］。对于带减速伞的弹药，降落伞主要起减速和调姿的作用，针对航空自导弹药的使用及总体要求，降落伞必须具有良好的稳定性、抗干扰能力和低空开伞性能，开伞动载小，包装体积也要小。

弹伞的稳定降落速度大小既影响落点散布，又影响弹体的入水过载以及留空时间。在相同条件下，入水速度越大，落点散布就越小、留空时间越短，但入水过载也越大，可能超出弹内装置的过载承受能力，因此要综合考虑稳定落速对二者的影响，既要兼顾到弹体强度、弹内装置的过载承受能力，确保弹药正常工作，又要尽量使弹药具有较高的落点散布精度和尽量短的留空时间，因此必须选择合适的弹体入水速度。

1.1 伞弹无风弹道数值仿真模型

低空投放带伞弹药系统，首先必须确保飞机和弹药的安全，因此通常采用延时开伞，即弹药在离开飞机到达安全区域后再通过控制系统延时打开降落伞。全弹道过程包括离机弹道(内挂时舱内复杂气流影响下的弹道或外挂时直升机悬翼气流影响下的弹道)、未开伞前的光体弹道、伞衣张满过程的开伞弹道以及伞衣完全张满后的弹伞弹道。本文采用简化的伞弹弹道仿真模型。即将复杂气流影响下的离机初始弹道在仿真模型中略去，以离机后的光体弹道作为起点。通过试验测试数据将离机参数作为仿真模型的初始参数，这样很大程度上降低了程序的复杂性并保证了仿真结果的可信度。伞衣张满过程也是一个复杂的气动力过程，很多学者对此作过大量的CFD仿真及建立非线性理论模型。通过对降落伞的吹风试验以及全弹道的投放试验我们发现，当降落伞的张满时间很短时，开伞过程简化为线性过程，假设伞衣面积线性增大且其阻力特征保持不变，即假设为降落伞的阻力线性增大的过程。这样十分有效地简化了开伞过程弹道的理论模型并较好地满足了工程实践的需要。对于伞衣张满后的伞弹弹道，参照文献［1］中导弹无动力无控弹道模型，并结合文献［2］中伞弹纵平面内二维弹道模型，采用相同的简化假设，拓展弹伞在水平面内的运动，即相应定义弹和伞的侧滑角，将弹伞弹道模型拓展为空间三维弹道，详细过程见文献［3］。

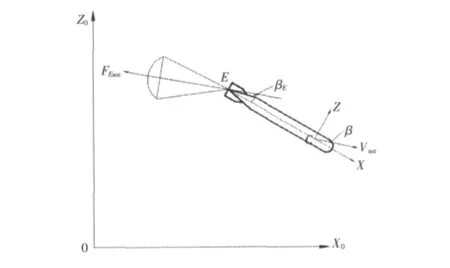
图1 水平面内弹伞系统运动示意图Fig.1 Horizontal plane motion of missile with parachute

1.2 风场模型

风是影响伞弹投放精度的重要因素，是伞弹系统飞行轨迹和飞行姿态的主要扰动源。因此，建立有效的风场模型进行弹道仿真，对有风影响时研究伞弹系统在风场中的运动特性具有重要意义。

由于大气运动的复杂性，我们无法对某一次投弹时的风速风向变化作准确的预测。工程实践中，由局部的实测数据，根据统计原理，对常值风和阵风进行估值。由于统计的风速仅为平均风速，工程实践中，通常把风速视为常值风和随机风的矢量和。

对于随机风，本文假设水平风的风速大小服从正态分布，均值由风级确定，方差由式(1)确定，并假设风向在水平面内均匀分布。

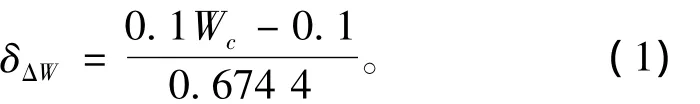
式中：δΔW为随机风速的标准差;Wc为常值风速。

1.3 数值方法

低空投放伞弹弹道仿真分为单发投放时的全弹道仿真及多发连投时的散布仿真。单发投放时的全弹道仿真伞弹弹道模型中弹体的位置坐标、速度、角速度、姿态角以及弹道角等均可表示为时间的一阶导数。对弹道诸元的求解是求解一阶常微分方程组的初值问题。本文利用MATLAB中求解一阶微分方程组的函数ode45，即4和5阶龙格－库塔法编程求解。程序由光体自由下落段、开伞过程段和伞弹减速稳定下落段组成，当调用第二段函数时须用第一段末端弹道诸元作为初值，同样调用第三段函数时用第二段末端弹道诸元作为初值。程序的计算终点为弹体入水时刻，因此在进行第三段弹道诸元求解时必须判断高度位置坐标的零点。通过调试首先将积分时间设定为足够长，在迭代过程中判断高度位置是否小于0(小于0为水面以下，与实际情况不符)，如果小于0则停止迭代，通过插值求取0点高度位置，进而确定水面落点的弹道诸元。

多发连投时，假设各随机因素均服从正态分布，则由正态分布的叠加性可知综合影响结果使落点仍服从正态分布。以单发投放时的全弹道模型为基础进行多次仿真(循环)并记录落点坐标，将各坐标点进行统计处理即可得出落点的散布规律。同时可以提取各弹道特征参数进行分析。由数理统计的精度要求适当选择计算的次数。

2 弹道测试技术

2.1 出舱过程测试

投弹时，弹舱处于打开状态，高速飞行下弹药在弹舱中受到较强的复杂气流影响，对于初始弹道的影响也十分复杂。因此，出舱过程弹体姿态的测试能深入认识弹舱复杂气流的影响。

测试方法采用一种既不需要改变飞机电气及机械接口，又能简单、可靠工作的新型飞机投弹出舱过程自动记录装置，满足飞机空投试验出舱过程记录的功能要求。系统主要由光敏开关、高速摄像机、电池组、转接适配器、高速摄像机安装架和遮光袋等组成(见图2)。

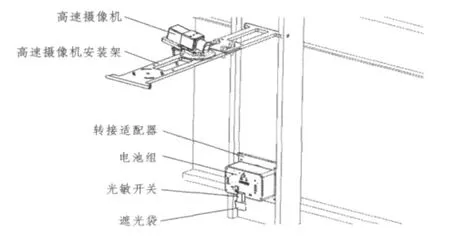
图2 飞机投弹出舱过程自动记录装置场景布置图Fig.2 Automatic recording devices for bomb extravehicular

2.2 低空外弹道测试原理

低空投放试验采用光测系统测试空中弹道参数。光测系统主要由2台电视跟踪测量仪、摄像机控制柜、图像处理计算机及方位标等组成。电视跟踪测量仪用来获得弹药在空中运动的原始图像，摄像机控制柜用来控制摄像机镜头使之随弹药的运动方向自动转动。图像处理计算机将摄像机获得的弹体运动原始图像，通过专用的图像处理软件，转换成弹体运动的弹道曲线。方位标用于跟踪摄像机的方位校准和初始对准。空中弹道测量采用2台电视跟踪测量仪交会的测量方法获取弹体运动的空中坐标参数，使用时在距离每台电视跟踪测量仪一定距离处设置2个方位标进行校准测量。

当跟踪摄像机镜头跟踪弹药运动目标时，各采样时刻的目标方位角和高低角都能获取，脱靶量与轴角编码器相对应的测量值合成便得到目标相对于测量站的角度测量值。在进行实时跟踪时，各采样时刻的无压缩数字图像和编码器的测量角度值以及采样时刻的绝对时间都同时记录下来，可进行脱靶量的事后高精度判读，从而获取高精度测角值，然后利用所测得的角度值进行交会计算得到目标位置信息。

3 仿真与测试对比分析

由于飞行的误差影响，通常试验前设定的初始参数如投弹速度、投弹高度与实际投放参数均有一定的差距，对于单发投放时测试结果与仿真数据比较分析，采用的方法是根据投放试验的测试初始参数确定仿真的初值，出舱过程的影响作为空中弹道的初始状态处理，即保证二者的初始状态一致。下面分别以无伞和伞弹弹道实测数据与理论值进行对比分析。

无伞弹道比较如图3～图5所示。

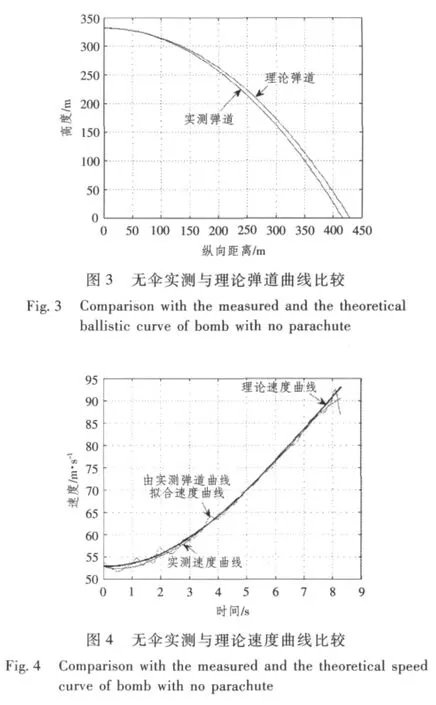
由图3～图5可看出，无伞时理论与实测弹道相比一致性很好。带伞弹道比较见图6～图10所示。

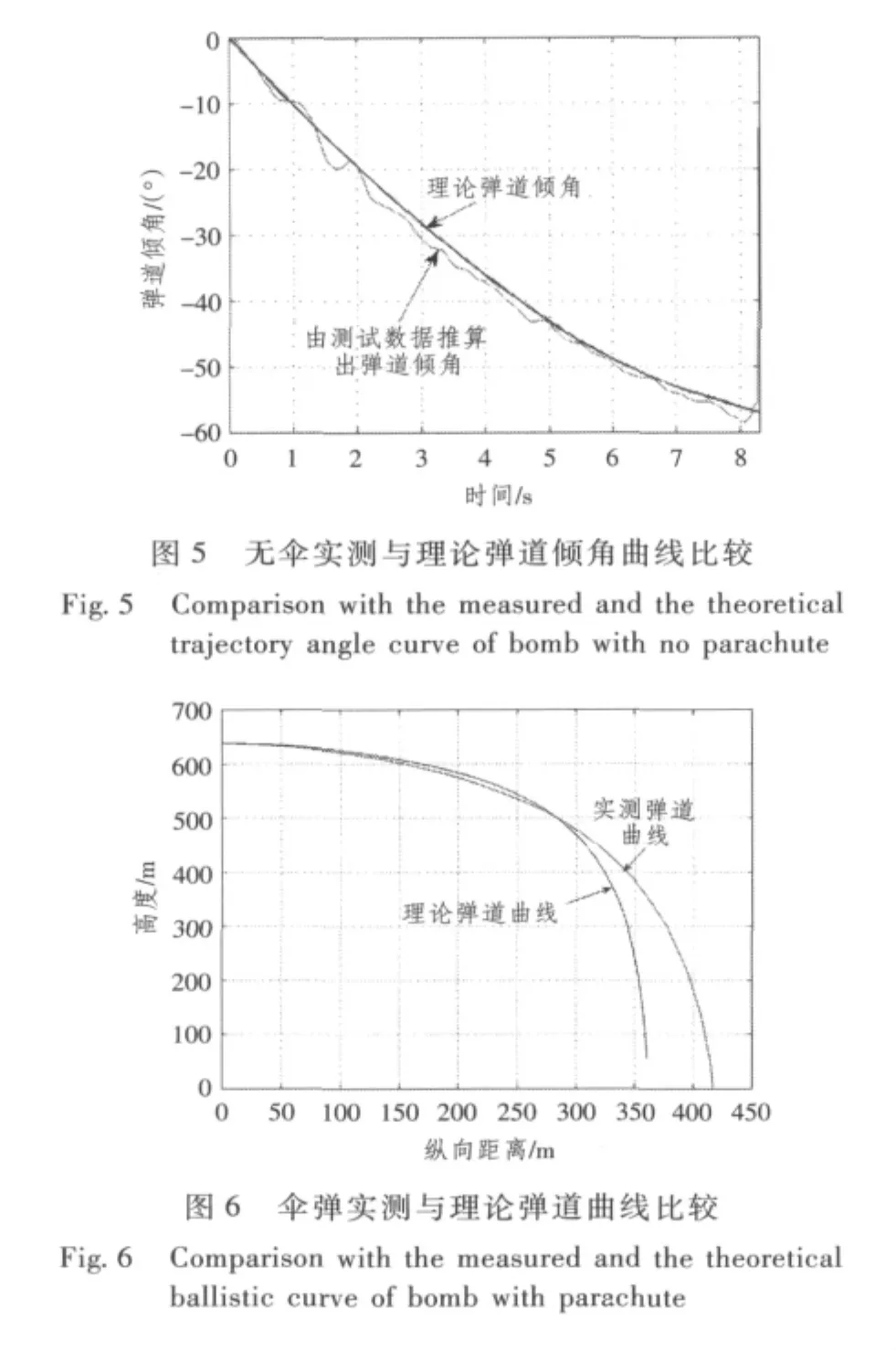
由图6可以看出，实测弹道曲线与理论弹道曲线有一定的偏差，表现为实际弹道射程偏远，并且到达地面的时间比理论值短。排除风等自然因素影响，导致射程增大留空时间变短的原因是降落伞的实际阻力特征比理论值偏小，同时将导致弹伞系统的稳定速度比理论值大，这可以由图3速度曲线得到验证。

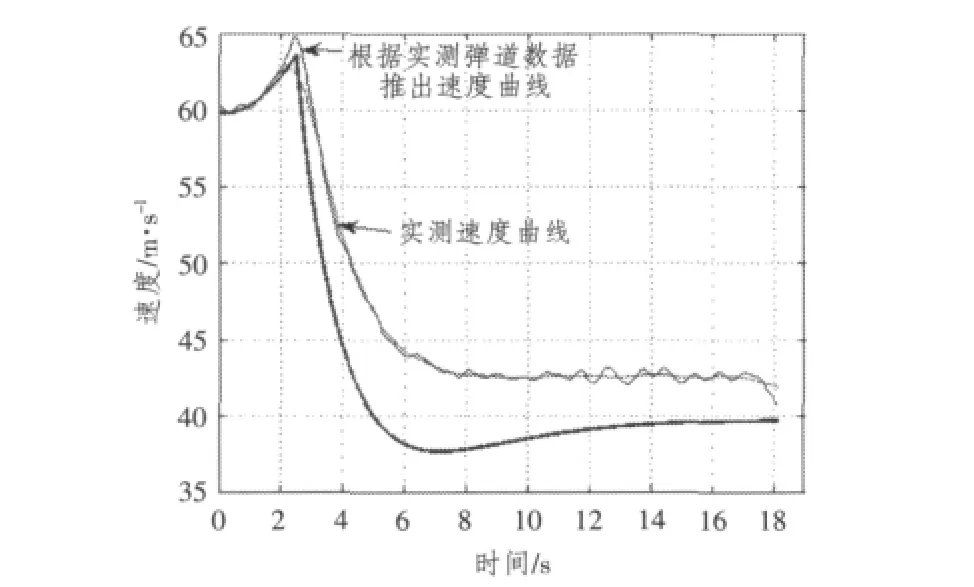
图7 伞弹实测与理论下落速度曲线比较Fig.7 Comparison with the measured and the theoretical speed curve of bomb with parachute

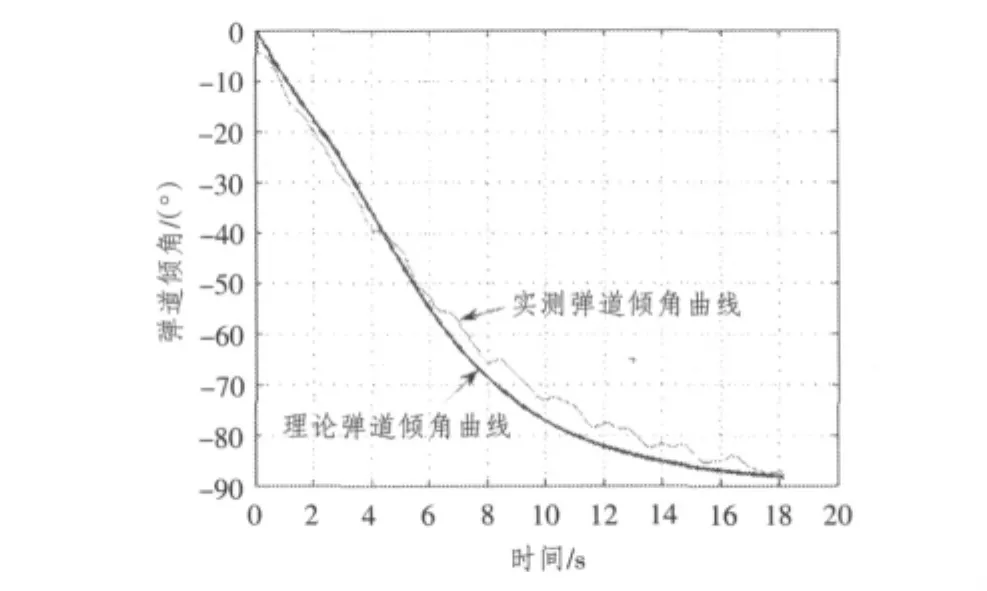
图8 伞弹实测与理论弹道倾角曲线比较Fig.8 Comparison with the measured and the theoretical trajectory angle curve of bomb with parachute

由图8可以看出，实测的弹道倾角曲线拟合后与理论值基本一致。弹伞系统稳定下落时弹体的攻角一般很小，近似认为曲线与弹体俯仰姿态角变化一致，因此也可以由此判定弹体的地面落角大小。由于光测系统不能直接测试弹体空中的姿态变化，由理论曲线的最终结果与高速摄影下的落角进行大致比较，可以验证仿真的正确性。

对于多发连投，通常我们更关注连投时的落点散布。实际投放试验很难得到散布结果，这是因为不可能在相同投放条件下(即同一次投放)投放足够多的试验弹。因此采用多次模拟投放对弹道散布进行分析。

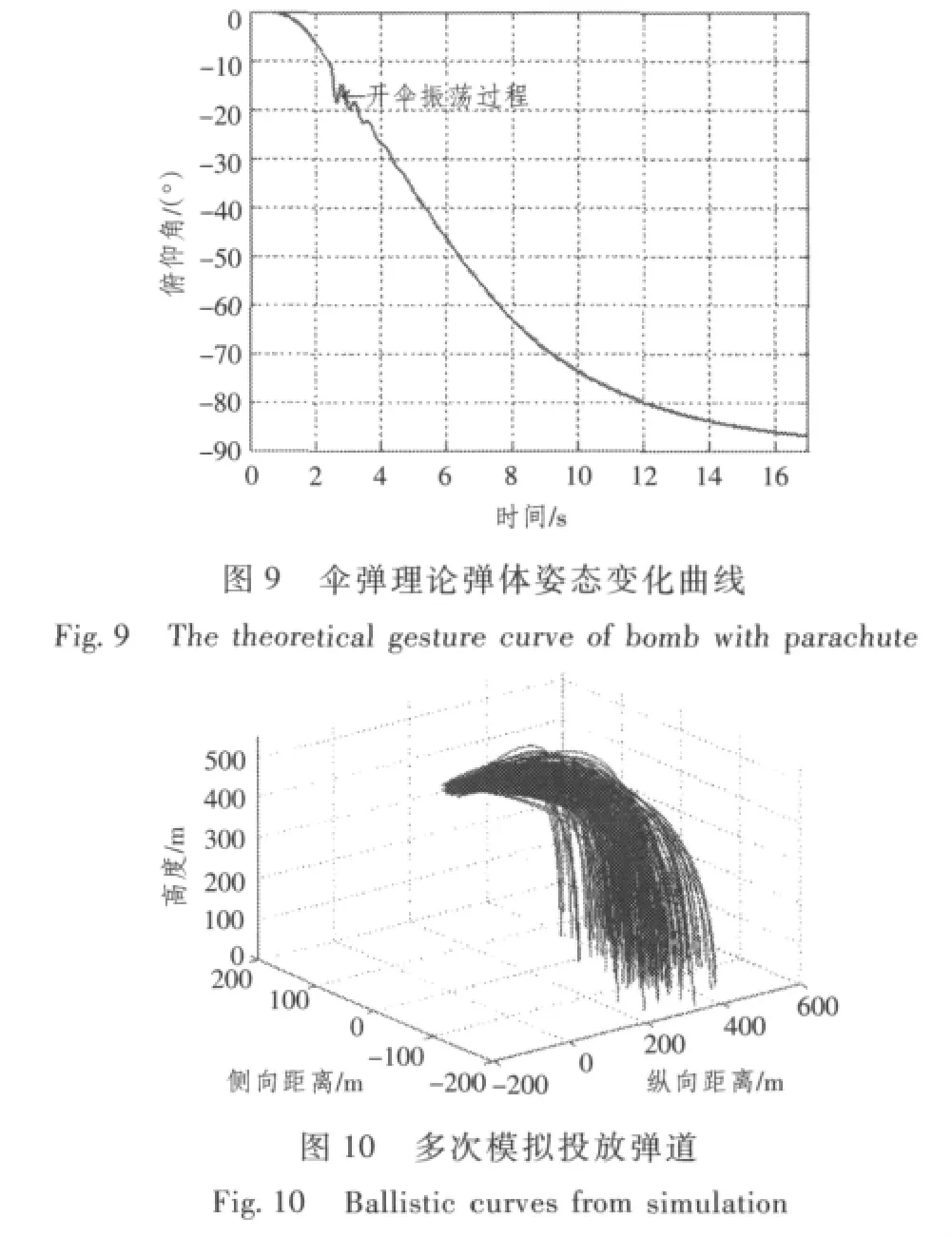
在实际投放试验中，弹伞运动的稳定性是导致实际弹道与理论弹道有差别的最大因素。弹伞运动不稳定的主要原因则是由减速伞导致，如弹伞连接旋转接头转动不灵活、伞绳缠绕、伞绳断裂、伞衣透气性差等因素引起。

4 结语

弹道仿真计算出的不仅是理论弹道，更是理想弹道，即在弹伞运动的动力学假设条件下，运动过程不受任何因素影响的弹道。实际投放时弹伞运动不光受自身加工误差影响，还受气候条件如风的影响。另外，主要影响因素还有投弹条件误差等。大多随机因素也为假设值，因此理论弹道与实际投放结果往往会有一定差别。弹道仿真作为武器装备研制的理论基础对研制初期有着重要的指导意义。同时，由实测弹道可对理论弹道进行修正。弹道仿真与试验的对比研究将为型号参数的确定及射表的编拟打下基础。

［1］钱杏芳，林瑞雄，赵亚男．导弹飞行力学［M］．北京：北京理工大学出版社，2006．

［2］张宇文．鱼雷弹道与弹道设计［M］．西安：西北工业大学出版社，1999．

［3］田应元，喻国兆，等．一种带减速伞的弹体三维弹道数值仿真模型［J］．舰船科学技术，2009，31(3)：143－146．

TIAN Ying-yuan，YU Guo-zhao，et al．A simulation model on 3D trajectory of missile with parachute［J］．Ship Science and Technology，2009，31(3)：143－146．

［4］田应元，侯小波，张翠兰．投弹条件对空投弹道落点散布的影响［J］．水雷战与舰船防护，2009，(1)：49－52．

［5］样世兴，李乃晋，徐宣志．空投鱼雷技术［M］．昆明：云南科技出版社，2001．

［6］王利荣，吴剑平．降落伞理论与应用［M］．北京：宇航出版社，1997．

Simulating and testing on trajectory of bomb under low altitude condition

WANG Xu-jun，TIAN Ying-yuan
(The 710 Research Institute of CSIC，Yichang 443003，China)

Aerial-launched bombs are the important part of advanced weapons，such as aerial bomb，earth penetrator，torpedo，mine and so on．Target accuracy and trajectory stability will affact the normal use and attack efficiency for weapon system．This paper created a simulating model of trajectory for bomb with parachute under low altitude condition．By the comparative study on theoretical trajectory and testing，it can determine the parameters and firing table，and it's very useful for aircraft ammunition on research and development．

trajectory parachute;simulation;testing

TJ65+5．2

A

1672－7649(2012)05－0113－04

10.3404/j.issn.1672－7649.2012.05.027

2011－08－30;

2011－11－21

王绪军(1973－)，男，高级工程师，主要从事水中兵器设计工作。