基于动态规划的反舰导弹火力分配优化方法
粘松雷,严建钢,陈 榕
(海军航空工程学院,山东 烟台 264001)
基于动态规划的反舰导弹火力分配优化方法
粘松雷,严建钢,陈 榕
(海军航空工程学院,山东 烟台 264001)
远程精确打击是反舰导弹攻击的必然趋势和高技术战场的主要特点。导弹攻击是打击敌水面舰船的主要手段,如何充分发挥反舰导弹的作战效能,减少不必要的浪费就成为战前制定作战方案以及实施作战指挥时必须解决的首要问题,而火力分配则是其中的一个重要环节。
反舰导弹;火力分配;动态规划
0 引言
“反舰导弹火力分配”是指根据导弹攻击的任务,合理进行目标配对决策,并向导弹装定相应的决策指令,依靠导弹自身的目标选择能力选择火分目标,实现上级的作战意图,保障作战协同[1]。其实质是按照指挥员的作战意图,合理分配导弹火力,打击预定目标。其实现形式主要体现在导弹的火分目标选择能力上,依靠导弹自主完成对目标的搜索、识别、选择和攻击,提高导弹的智能化作战水平。
1 火力分配数学模型的建立
1.1 作战想定
红方对蓝方舰艇编队实施超视距多弹饱和攻击,蓝方舰艇对来袭反舰导弹实施硬拦截和软对抗;在攻防过程中不考虑蓝方对红方的导弹反击[2]。
红方编队对蓝方编队导弹攻击时的火力分配,需解决以下2个问题:
1)为了达到对蓝方编队预定的毁伤指标,如何合理部署红方导弹兵力,才能使红方消耗的导弹价值最小;
2)红方如何合理分配导弹,才能使其对蓝方编队造成的毁伤程度最大,即使红方导弹的作战效能最大化[3]。
可见,红方与蓝方的攻防对抗问题是具有目标价值收益最大、耗弹量成本最少的约束条件众多而复杂的优化问题,该问题是多目标和多约束的优化问题,即多目标优化。MO问题需要优化一组费用函数,其解不是单一点,而是一组点的集合,称之为Pareto 最优集[4-5]。
1.2 数学模型的建立
红方多种型号的反舰导弹对蓝方舰艇编队实施饱和攻击。假设i为导弹的型号;λi为1枚第i类导弹的价值系数;j和r为目标的批号;Ni为第i类导弹的数量;xij为第i类导弹用于射击第j批目标的数量;xj为射击第j批目标的导弹总数;vr为第r批目标的价值系数;ωir为第i类导弹按照毁伤指标,毁伤第r批目标所需的导弹数;Pijr为第i类导弹对第j批目标射击时对第r批目标的命中概率;ki为第i类导弹的价值系数。
根据作战想定可以建立导弹攻击火力分配问题的规划模型如下:
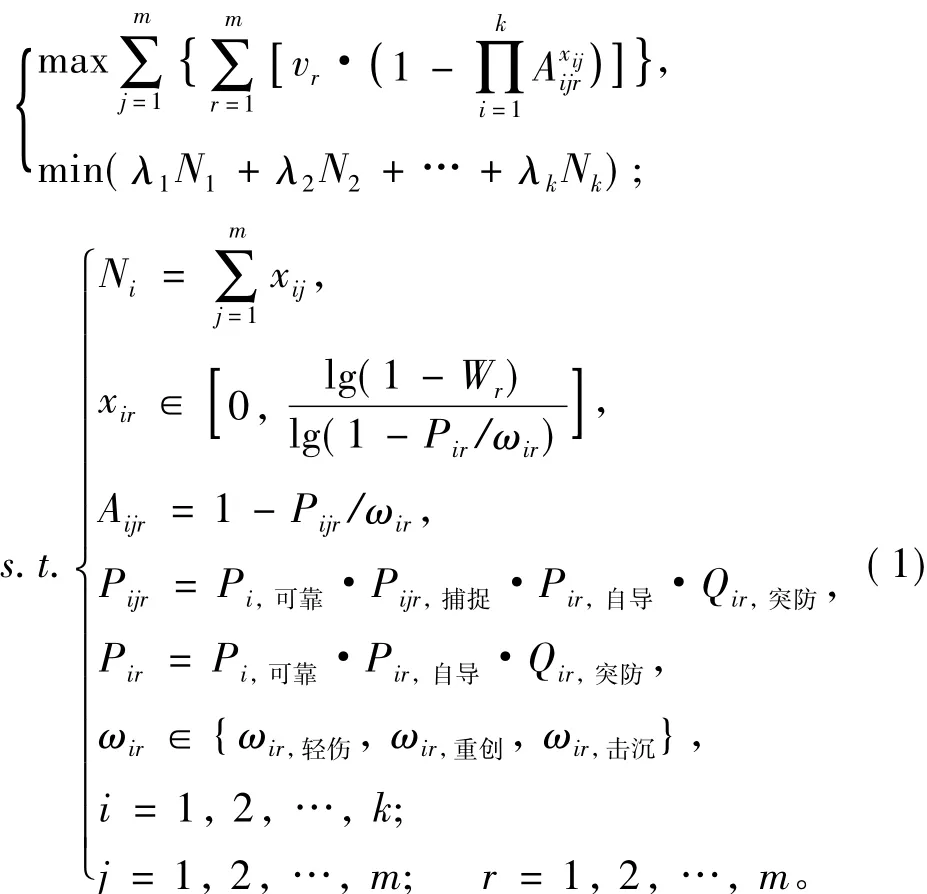
式中:Pi,可靠为第i类导弹的可靠飞行概率;Pijr捕捉为第i类导弹对第j批目标射击时,对第r批目标的捕捉概率;Pir自导为第i类导弹对第r批目标射击时的自导命中概率;Qir,突防为第i类导弹对第r批目标射击时的突防概率。ωir,轻伤为第i类导弹轻伤第r批目标平均所需的导弹数;ωir,重创为第i类导弹重创第r批目标平均所需的导弹数;ωir,击沉为第i类导弹击沉第r批目标平均所需的导弹数。
因为反舰导弹末制导雷达对某批目标的捕捉概率具有很大的不确定性。为此,在不考虑反舰导弹的目标捕捉概率Pijr捕捉对作战效能影响的情况下,可将式(1)进一步简化为:
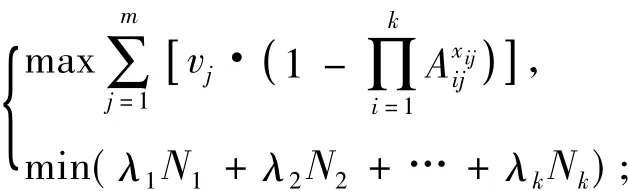
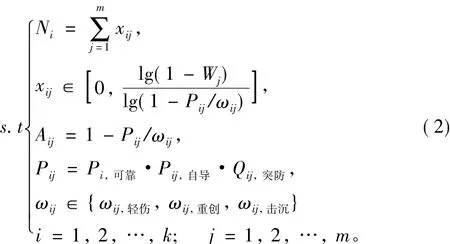
2 基于动态规划算法的火力分配优化方法
动态规划是运筹学的一个分支,是求解决策过程最优化的数学方法[4]。20世纪50年代初,美国数学家R.E.Bellman等在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,把多阶段过程转化为一系列单阶段问题,逐个求解,创立了解决这类过程优化问题的新方法——动态规划[6]。
多阶段决策过程是指这样一类特殊的活动过程,它们可以按时间顺序分解成若干相互联系的阶段,在每个阶段都要做出决策,全部过程的决策是一个决策序列[7]。要使整个活动的总体效果达到最优的问题,称为多阶段决策问题。虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
2.1 基本假设
在反舰导弹的数量较多、型号单一时,可采用动态规划算法优化火力分配,使导弹群的整体作战效能最大化。采用动态规划算法进行火力分配优化,需基于如下3点假设:
1)对每个目标射击时,不存在火力转移问题;2)参与攻击的反舰导弹均为同一型号;
3)反舰导弹总数量不足以对所有被攻击目标舰艇同时实施饱和攻击。
这3点假设对应的数学描述为

其中:i=1,2,…,k;j=1,2,…,m;r=1,2,…,m。虽然导弹火力分配问题是个多目标优化问题,但依据假设将参与攻击的反舰导弹总数量常数化了,因此多目标优化问题即转化为单目标函数的非线性规划问题,如式(4)所示。
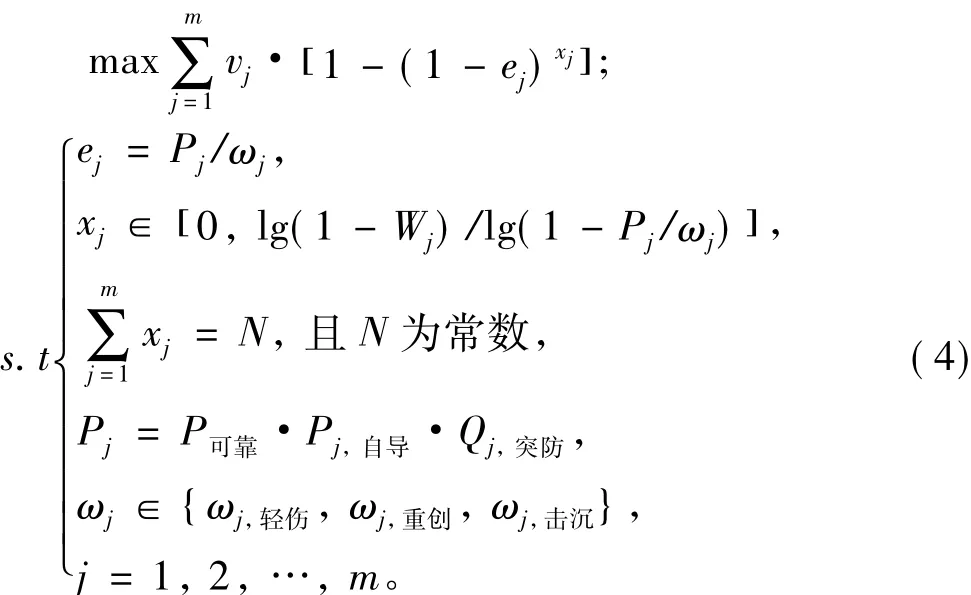
2.2 模型解算过程
动态规划问题的求解过程共分5步:
1)根据所给问题,将过程恰当地分为若干阶段(一般根据时间和空间来划分),即把导弹的火力分配过程看作是有次序地将导弹分配给第1、第2,…,第m个目标的过程,且把分配给第j个目标的过程作为第j个阶段,这样就把导弹火力分配过程转化为相互联系的m个阶段。
2)正确选择状态变量来描述过程及其在各个阶段的状态。动态规划中的状态概念,必须满足“无后效性这样一个条件”。所谓无后效性是指,如果给定了某一阶段的某一状态,则其后续过程的发展不受该状态以前各阶段状态的影响。这也就是说,过程的状态不影响它未来的发展。
设状态变量Sj为分配给第j个目标到第m个目标的导弹总数,即j阶段初所拥有的导弹数。显然,0≤Sj≤N。
3)确定决策变量及每段允许决策集合。
决策变量xj为分配给第j个目标的导弹数,0≤xj≤Sj(即允许决策集合)。
4)建立状态转移方程。
一般来说,对于j阶段某一给定的状态Sj,只要决策变量xj一经确定,其下一阶段的状态变量值Sj+1也就完全确定。因此,可建立Sj+1随Sj和xj变化的对应关系,这种状态转移的规律,可用式(5)表示Sj+1与Sj和xj之间的函数关系,称为状态转移方程,即

则该导弹火力分配问题的状态转移方程为

5)根据题意列出指标函数,该指标函数要满足递推性。
用阶段毁伤效能函数gj(Sj,xj)表示对第j个目标分配xj枚导弹后所得到的毁伤效能,最优效能指标函数fj(Sj)为将Sj枚导弹分配给第j个目标到第m个目标后,所获得的最优毁伤效能。其动态规划的递推关系为

按照以上5个步骤,用递推方法,先求后部最优子策略,然后逐步向前递推得全过程的最优策略。
3 实例分析
设红方飞机编队在一次突袭中使用8枚某型反舰导弹对蓝方水面舰艇编队实施攻击,蓝方编队由1艘大型补给船T1、1艘驱逐舰T2、1艘护卫舰T3和另外1艘护卫舰T4组成。蓝方舰艇的价值系数为vj,单枚XX型导弹对单艘目标舰艇的毁伤概率为ej,如表1所示。
依据递推关系式(7)及表1的数据,求解最优火力分配方案,其中,导弹数N=8;目标数m=4。
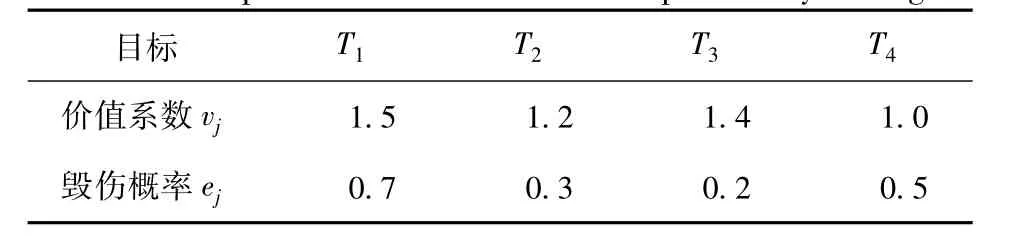
表1 目标舰艇的价值系数和毁伤概率Tab.1 Important coefficients and kill probability of targets
1)当j=4时,S4=0,1,…8;X4=0,1,…8;该阶段最大毁伤效能为

2)当j=3时,S3=0,1,…8;即S3枚导弹分配给第3和第4个目标,最大毁伤效能为
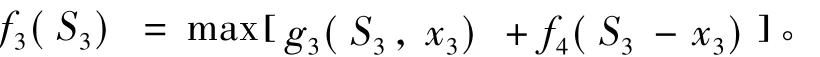
3)当j=2时,S2=0,1,…8;S2枚导弹分配给第2、第3和第4个目标,最大毁伤效能为
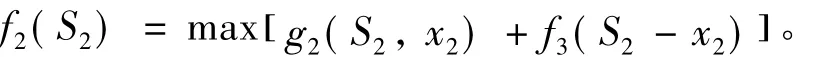
4)当j=1时,只有S1=8,即8枚导弹分配给第1、第2、第3和第4个目标,最大毁伤效能为

鉴于文章篇幅问题,这里仅给出j=1时的计算结果,如表2所示。
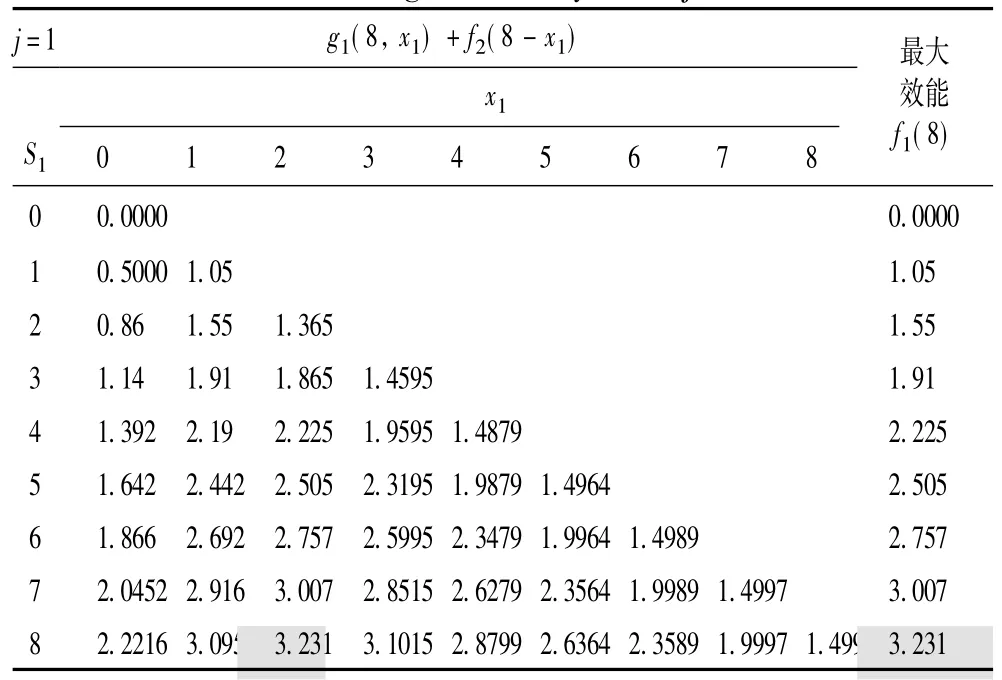
表2 j=1时的阶段效能Tab.2 Stage efficiency when j=1
由表2可知,最大毁伤效能指标为f1(8)=3.231,此时决策变量x1=2,即对第1个目标发射2枚反舰导弹。然后,按j=2,j=3,j=4的顺序逆推,从而求得导弹最优分配方案为:X1=2,X2=2,X3=2,X4=2。导弹的火力分配矩阵为[2,2,2,2],即对大型补给船T1、驱逐舰T2、护卫舰T3和护卫舰T4分别发射2枚导弹,实施攻击所获得的综合毁伤效能最大。
4 结语
本文在作战想定的基础上,建立反舰导弹群攻击火力分配问题的完整数学模型;并运用动态规划算法对火力分配的数学模型进行了优化研究,在实例中证明了数学模型和优化算法的正确和可行性。
[1]杨祖快,刘鼎臣.反舰导弹自主式火力分配[J].火力与指挥控制,2005,30(2):1 -4.
YANG Zu-kuai,LIU Ding-chen.Study on anti-ship missile firepower distribution[J].Fire Control and Command Control,2005,30(2):1 -4.
[2]滕克难.舰空导弹系统抗饱和攻击反导作战效能评估[J].弹箭与制导学报,2005,25(3):37 -39.
TENG Ken-nan.Effectiveness evalaution of anti-missile saturation attack for the ship-to - air missile[J].Arrow and Guidance Transaction,2005,25(3):37 -39.
[3]张年春,沈培华.编队导弹攻击的火力分配研究[J].战术导弹技术,2007,(3):36 -39.
ZHANG Nian-chun, SHEN Pei-hua.Researchonfire disposition model for formated anti-ship missile[J].Tactical Missile Technolog,2007,(3):36 -39.
[4]王小平,曹立明.遗传算法-理论、应用与软件实现[M].西安:西安交通大学出版社,2002.115-121.
WANG Xiao-ping,CHAO Li-ming.Inheritance algorithmtheory,application and software realization[M].Xi'an:Xi'an Traffic University Publishing House,2002:115 -121.
[5]崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社,2006.40-50.
CUI Xun-xue.Many objectives evolution algorithm and application[M].Beijing:National Defense Industry Publishing House,2006:40-50.
[6]张最良,李长生,等.军事运筹学[M].北京:军事科学出版社,1999.50-56.
ZHANG Zui-liang, LIChang-sheng, etal. Military operations research[M].Beijing:Military Science Publishing House,1999.50 -56.
[7]谢春燕,李为民,刘付显.整数规划与动态规划在防空导弹火力分配中的应用研究[J].弹箭与制导学报,2003,23(4):72-75.
XIE Chun-yan, LIWei-min, LIU Fu-xian.Integer programming and dynamic programming to airforce missile firepower allocation[J].Arrow and Guidance Transaction,2003,23(4):72-75.
The optimization method of antiship missile fire distribution based on dynamic programming
NIAN Song-lei,YAN Jian-gang,CHEN Rong
(Naval Aeronautical Engineering Institute,Yantai 264001,China)
The long-range accurate stike is the certain trend of antiship missile attack and the major characteristic of high technology battlefield,the missile attack is the major means hitting enemy's surface ships,how to sufficiently elaborate the operation efficacy of antiship missileand reduce unnecessary waste is the first importance question which must be solved in course of action and operational command,while the fire distribution is the important link.
antiship missile;fire distribution;dynamic programming
E927
A
1672-7649(2012)07-0110-04
10.3404/j.issn.1672-7649.2012.07.025
2011-08-01;
2011-10-12
粘松雷(1982-),男,博士研究生,研究方向为海军兵种作战数理战术分析。

