高频雷达信号的双线性时频分布性能研究＊

施 华 黄麟舒

（1.海军七○二厂 上海 200434）（2.海军工程大学电子工程学院 武汉 430033）

1 引言

高频地波雷达可以用来测量低速移动的目标和海洋的动力学参数。由于目标的散射截面较小，可以采用长相干积累时间来提高信噪比和保证足够的多普勒频率的分辨率。然而实际上，目标一般在被监测时不是匀速运动的，而是变速运动的，此时，目标信号就成了时域非平稳信号。时频分析法是非平稳信号处理的一个重要分支，它是利用时间和频率的联合函数来表示非平稳信号，并对其进行分析和处理［1～5］。

相比于处理经典平稳信号的常用方法傅里叶变换，时频分析方法可有效克服传统傅里叶变换的这种全局性变换的局限性，按照时频联合函数的不同可以分为线性时频表示和双线性时频表示两种。

线性时频表示主要有短时傅里叶变换、Gabor展开以及小波变换等。而双线性时频表示反映的是信号能量的时频分布，也称二次型时频表示，主要有Cohen类时频分布和仿射类（Affine）双线性时频分布，其中有著名的是 Wigner－Ville分布。

Wigner于1932年提出了Wigner分布，最初应用于量子力学。1948年，Ville将其引入信号分析领域。1970年，Mark提出 Wigner－Ville分布中最主要的缺陷—交叉干扰项的存在。1980年，Claasen和 Mecklenbraker联合发表的论文中详细论述了Wigner－Ville分布的概念、定义、性质以及数值计算等问题。

本文从高频地波雷达目标探测的实际出发，分析了双线性时频分析，给出了Wigner－Ville分布的仿真结果，研究了核函数削弱交叉项问题的作用。

2 海杂波干扰分析

但在多变的海杂波环境下，基于统计理论的经典检测方法往往需要较高的信杂比才能检测到目标，很难在较小的虚警概率情况下准确检测到弱小目标。并且海杂波往往随着时间和空间的不同而发生变化，具有很强的非平稳特性，海杂波的时变特性使得单一的统计分布模型往往不能充分描述出海杂波的物理特性。

时频分布是非平稳信号的一种非线性变换，从时频分布的角度来描述海杂波，通过时频变换将一维的时间信号转换为二维的时间频率图像，从而提取出有用的图像特征以区分杂波和信号，达到检测的目的［6～9］。

海杂波可视为由许多不同幅度、不同相位的“点”散射体回波叠加合成，而“点”散射体的大小可以根据方位分辨力以及满足的随机分布来确定。设第l个距离单元由N个“点”散射体，第i个“点”散射体的多普勒频率分别为fdpi和fdni，则经过混频、低通滤波以及距离维FFT后，第k个通道、第m个调频周期的海杂波信号可以表示为

式中，αi（k，m）和ρi（k，m）分别为朝向和背离雷达运动的海杂波幅度，φki为第i个“点”散射体到第k个发射阵元波程（以发射阵中心为参考）引起的相位差。

3 二次型时频表示

二次型时频表示所反映的是信号能量的时频分布。二次型时频表示不满足线性叠加性、假设：

记x（t），x1（t），x2（t）的线性时频表示分别为P（t，f），P1（t，f），P2（t，f）

则有：

最后一项称为干扰项，这是二次型时频表示固有的一个属性。

在考虑目标的加速运动时，目标的信号频谱是一个时变信号，考虑用时频分析的方法。用来进行时频分析的传统方法是STFT，它的局限性在于它是对时间分辨率和频率分辨率的一种折中。一个基本的解决方法是采用时频函数，即一种用来同时描述信号在时间和频率两个方面的瞬时能量密度或强度的分布函数。一般来说，常用的分布函数可表示为

式中，上标 ＊ 表示复共轭；η和τ分别表示时间和频率变量；Af（.）是模糊函数；φ（η，τ）是核函数。当φ（η，τ）＝1 时，上式表示的是前面提到的最有名的时频分析函数Wigner－Ville分布（WVD），即

尽管WVD具有好的时频聚集性，或说最佳的时间和频率分辨率，但在处理多分量信号时，根据卷积定理，它存在交叉项，产生“虚假信号”，即交叉项所表示的时间和频率特性在实际中是不存在的。

交叉项是二次型时频分布的固有结果，它来自于多分量信号中不同信号分量之间的交叉作用。时频分布的交叉项一般是比较严重的，交叉项通常是振荡的，而且幅度可达到自主项的两倍，造成信号的时频特征模糊不清。因此，如何有效抑制交叉项非常重要。

目前，文献提出抑制或削弱交叉项的方法，主要有：加核函数法，预滤波法，多分量分离法与辅助函数法等。由于交叉项的抑制主要通过核函数的设计来实现，

常用的加核函数后的Wigner－Ville分布主要有以下几种：伪 Wigner－Ville分布（PWD），平滑 Wigner－Ville分布（SWD），平滑伪 Wigner－Ville分布。本文主要讨论几种核函数对抑制交叉项的作用。

4 仿真结果分析

常采用核函数对 Wigner－Ville分布进行平滑，其目的是抑制Wigner－Ville分布的交叉项。基于此，Cohen类时频分布是为了较小 Wigner－Ville分布的交叉项而提出的。由于是平滑，自然在平滑交叉项的同时也会对信号项有磨损效果，从而降低时频聚集性，时间分辨率和频率分辨率变差。

4.1 Wigner－Ville分布

图1 线性调频信号的WV分布（等高线图）

典型的Cohen类时频分布就是Wigner－Ville分布。图1和图2是某离散信号的 Wigner－Ville分布的计算结果，由图1可以明显看出，信号的频率是随时间线性变换的，与理论值是一致的，这说明Wigner－Ville分布能揭示信号能量在时频面上的分布情况。

图2 线性调频信号的WV分布（三维图）

4.2 抑制四分量信号的交叉项

对于多分量信号，必然存在交叉项，因为分布是信号的二次变换，分量之间存在自身项和交叉项。但不管分量之间的时频距离大小是多少，交叉项都不会消失。Wigner－Ville分布交叉项的特点可归纳为：两个分量会在它们的几何中点处产生第三个交叉项分量，除此之外，交叉项会在连接这两点的直线上产生振荡，振荡频率与这两点之间的距离成正比。

图3 四分量信号的时域波形

由于核函数对 Wigner－Ville分布起平滑作用，最终目的是抑制Wigner－Ville分布的交叉项，因此，下面讨论几种核函数的选择对于抑制交叉项和时频聚集性两者之间的一个好的兼顾。

产生的多分量信号波形如图3所示，其 Wigner－Ville分布如图4所示，而 其 Wigner－Ville分布如图5所示。图4看到，在时频面上本不应有能量的地方存在很多交叉项，这是由于Wigner－Ville分布的双线性造成的。比较图4和图5可见：在四分量信号的伪Wigner－Ville分布中抑制了部分交叉项。

图4 四分量信号的 W－V分布

图5 四分量信号的伪W－V分布

由于自身项集中在原点处，而交叉项不在原点处，因此，当两个信号的强度相当时，交叉项在两者的中间，这样通过设计滤波器可以分开信号的自身项与交叉项，但当两个信号的强度相差较大时，交叉项靠近弱信号那边，这样会掩盖弱信号的自身项。在多目标的情况下，采用伪Wigner－Ville分布抑制交叉项作用较强。

4.3 抑制二分量信号的交叉项

图6 二分量信号伪 W－V分布

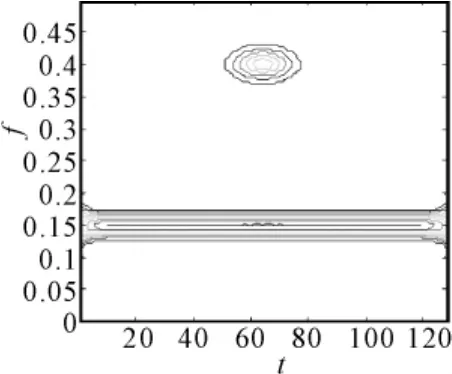
图7 二分量信号平滑伪W－V分布

当信号为二分量时，其伪 Wigner－Ville分布仿真结果如图6，平滑伪Wigner－Ville分布如图7，比较图6和图7，在Wigner－Ville分布中能看见两个信号的自主项以及交叉项，由于交叉项只在时间轴上振荡，因此频域平滑的伪Wigner－Ville分布降低了频率分辨率，而且不能抑制交叉项，而平滑伪Wigner－Ville分布进行了时域平滑，因此降低了交叉项的影响。

5 结语

本文针对高频地波雷达对非平稳目标检测问题，采用双线性时频分布研究在海杂波背景中检测多分量目标的问题。讨论了几种 Wigner－Ville分布，分别在频域或时域平滑后，抑制多分量目标的交叉项的作用。其中伪 Wigner－Ville分布较纯Wigner－Ville分布的抑制作用较大，而平滑伪Wigner－Ville分布的效应又较伪 Wigner－Ville分布大。不过利用窗平滑可以抑制交叉项，但也带来不足，如不能满足原有 Wigner－Ville分布具有的边缘性质等，如何均衡这两方面，将在下一步工作中继续研究。

［1］Armstrong B C，Griffiths H D.CFAR detection of fluctuating targets in spatially correlated K－distributed clutter［J］.IEE Proc.，1991，138（2）：139－152.

［2］A M Sayeed，D L Jones.Optimal kernels for nonstationary spectral estimation［J］.IEEE Trans.SignalProcessing，1995，43：478－491.

［3］A Yasotharan，T Thayaparan.A time－frequency method for detecting an accelerating target in sea or land clutter［J］.IEEE Trans.AES，2006，42（4）：1289－1310.

［4］Qian S.Time－frequency and wavelet transforms［M］.Prentice－Hall Inc，NewYork，USA，2002：20－35.

［5］Rifkin R.Analysis of CFAR performance in Weibull clutter［J］.IEEE Trans.AES，1994，30（2）：315－328.

［6］Nogara T J，Haykin S.Canadian east coast radar trials and the K－distribution［J］.IEE proceedings－F，1991，138（2）：80－88.

［7］Joughin I R，Percival D B，Winebrenner D P.Maximum likelihood estimation of K－distribution parameters for SAR data［J］.IEEE Trans.Geosci.Remote Sensing，1993，31：989－999.

［8］杜鹏飞，王永良.海杂波背景中的一种恒虚警率检测方法［J］.国防科技大学学报，2005，27（3）：54－57.

［9］陈新敏，张明博.基于时频分布的海杂波背景下的小目标物检测［J］.制导与引信，2008，29（2）：44－48.

［10］朱玉鹏，王宏强，肖顺平.基于自适应核时频分布的机动目标ISAR成像［J］.现代雷达，2009，31（3）：38－42.