基于瞄准多个目标航天器的空间拦截器停泊轨道优化
杨 亮,武 健,向明思
(第二炮兵工程大学906 室,西安 710025)
空间是未来的战略高地,谁控制了太空,谁就占据了主动。空间拦截与反拦截的不断发展将使空间争夺战更加激烈。空间停泊武器能有效拦截敌方外层航天器,它是各国争相发展的对象。
当前国内学者对空间停泊武器的研究主要集中于对单个目标航天器的机动拦截上。美国著名的“智能卵石”计划主要使拦截器小型化、轻型化且制导性能更优并使其在空间大量部署。本文有别于此,探讨单个拦截器预备拦截一组多个目标的停泊轨道优化研究。
考虑为未来空间争夺战节约资源、提高效率的设想,现假定某一在停泊轨道上正常运转的空间拦截器预备瞄准一组多个目标,当命令下达后攻击一个特定目标。由于目前近地轨道上各种非合作航天器数目众多,且有部分轨道部署比较集中,所以本文设想可以实现。于此,本文应用固定时间最小能量机动拦截模型并设定停泊轨道参数变化值域及解算步长,通过改进遗传算法对每次步长进行仿真计算,得到最小的速度增量累加值,最后找到一条满足任务约束的能量最优的拦截器停泊轨道。
1 固定时间最小能量拦截模型
在此只考虑椭圆轨道情况且假定地球为均质圆球,拦截器通过脉冲作用获得瞬时速度增量及在拦截过程中不考虑摄动因素影响。
拦截过程如如图1 所示,拦截器运行初始轨道为轨道Ι,t 时刻拦截器的位置矢量和速度矢量分别为r1和v1,假定在该时刻对其施加速度冲量Δv,使拦截器的速度矢量变为ν2,并进入另一条轨道F,经Δt 秒后命中预定的空间位置矢量为vm的目标卫星。
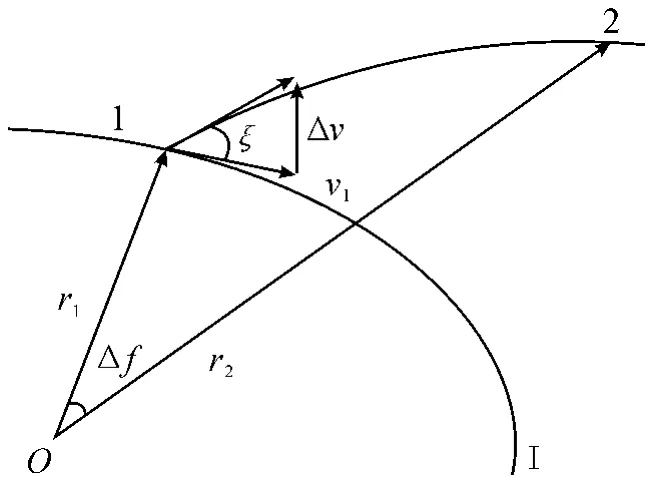
图1 轨道拦截示意图
记轨道F 的半通径为P2,偏心率为e2,则r1和r2的夹角为Δf(即真近点角之差):
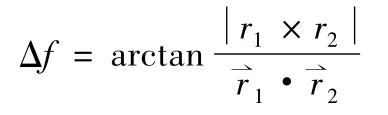
设定
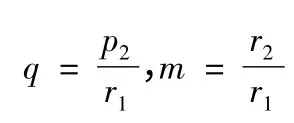
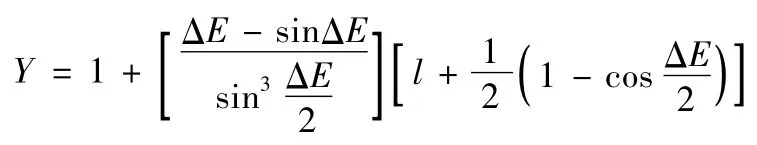
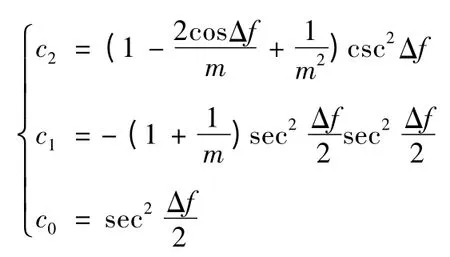
根据活力公式及动量守恒定理即可计算v2(Θ2为终极轨道的速度倾角)
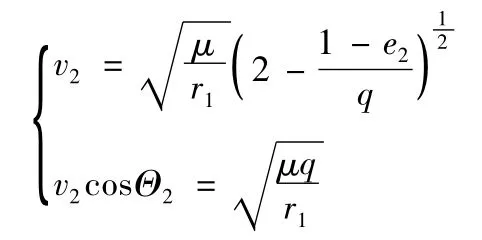
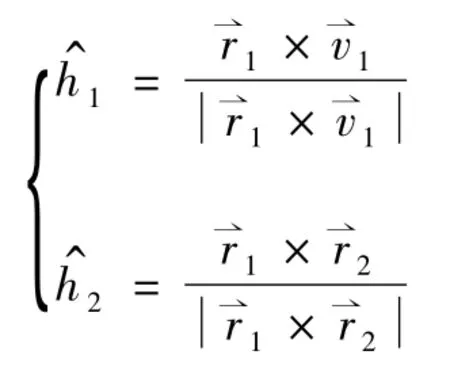
则初、终轨道的夹角
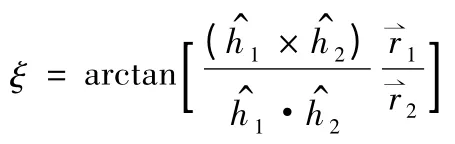
又已知Θ1为初始轨道弹道倾角

最终得到轨道坐标系下的Δv
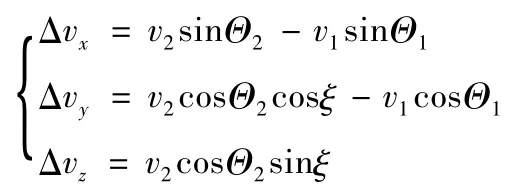
2 改进遗传算法思想及设计
为提高搜索的速度和搜索的精度,现对遗传算法进行改进。由于遗传算法的优点是全局搜索能力比较强,但它在局部搜索方面能力比较弱,搜索出的优化结果带有随机性,不一定能够得到准确的全局最优解。又由于传统的优化方法如梯度法、爬山法、方向加速法等都有很强的局部搜索能力,故将传统的优化方法嵌入到遗传算法中,使之能够同时具有好的全局和局部搜索能力。
2.1 问题解的基因表示
顾及一组目标的情况下,基因表示为拦截器在独立攻击各个目标航天器的变轨时刻tm(m =1,2,…)及拦截时刻tmh(h=1,2,…)。由于此时编码的范围较大,且精度和运算速度要求都有所提高,所以这里选用浮点数编码。
2.2 适应度函数
要求机动变轨到各个目标所耗能量累加最小为最优,故遗传算法的适应度函数可表示为3,…。
约束条件为hi(X)≤0,i=1,2…,则设惩罚函数:
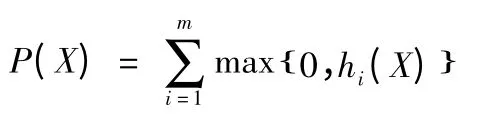
考虑惩罚函数后,广义的适应度函数可以定义:
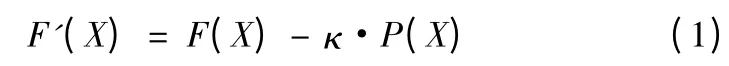
式(1)中,κ 为惩罚函数作用强度的系数,κ >0 且当κ→+∞时,广义适应度函数将收敛到原问题的解。但在实际运算中,如果惩罚函数的强度太小的话,就有可能使个体的适应度差异不大,降低了个体之间的竞争力,从而影响遗传算法的运行效率;惩罚函数的强度太大的话,部分个体又有可能破坏约束条件,不能保证优化所得到的个体一定是满足约束条件的可行解,在此处取κ=1。
最后,在上述设置下,广义适应度函数:
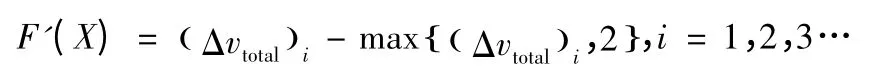
2.3 嵌入优化方法选择
方向加速法具有很好的局部搜索功能,该方法不需要计算目标函数的梯度,且具有完善的理论体系,很适合本问题的优化。在已经完成遗传操作的群体中选取某些个体应用方向加速法进行局部寻优,以优化后的结果作为新的染色体,能有效改善群体的性能。选取的数目越多,优化效果也就越好,但也会带来计算量的加大,因此本节选取群体中适应度值较小的n 个个体进行计算。
2.4 遗传操作
选择算子。这里采用比例选择法选取适应度值较小的个体以一定的概率遗传至下一代。设群体的大小为M,个体i 的适应度为Fi,则个体被选中的概率pis:
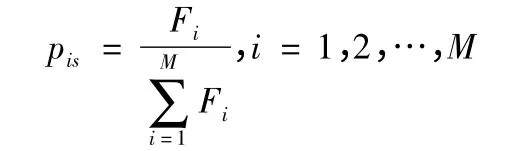
交叉算子。这里采用非均匀算术法,即设XkA,XkB为第k代的两个个体,则经交叉运算后产生的两个新个体:
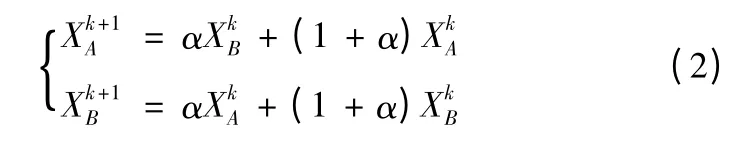
式(2)中,0 <α <1 随着遗传代数的增大,α 逐渐接近于0。
变异算子。这里采用非均匀变异法,即设X =x1x2…xk…xl为将要进行变异的个体,变异点为xk,xk处基因值的取值范围为则新的基因值x'k的产生方法:
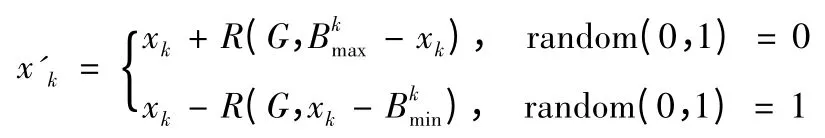
G 为当前的遗传代数;R(G,y)为一产生非均匀随机数的函数,随机数的取值范围为 [0,y],且随着G 的增大,R(G,y)接近于零的概率也逐渐增加。
3 停泊轨道优化解算流程
设计停泊轨道优化解算流程如图2 所示。
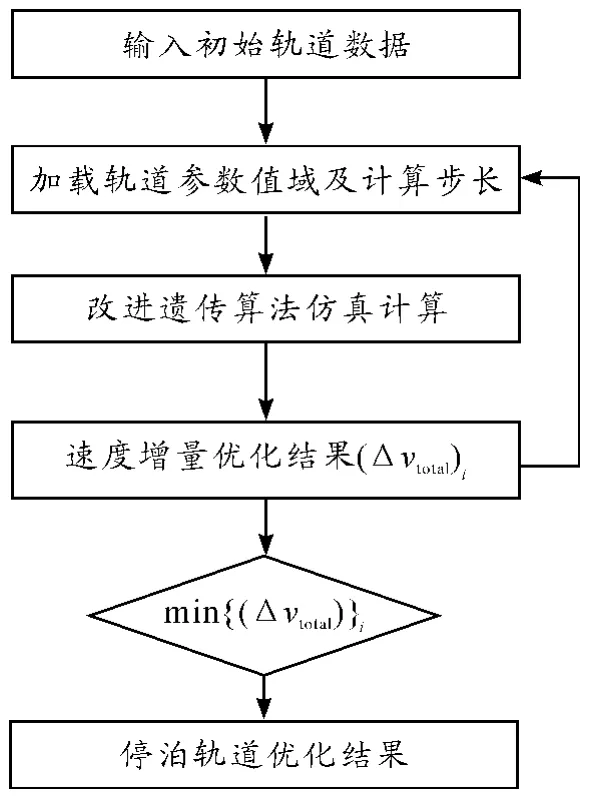
图2 停泊轨道优化解算流程
优化解算流程:
1)输入空间拦截器及一组多个目标航天器的轨道数据。目标航天器轨道数据选定如表2 所示,拦截器初始轨道数据根据多次试验结果获得。
2)设定拦截器轨道参数变化值域及步长。这里根据文献[7]中的结论,选定
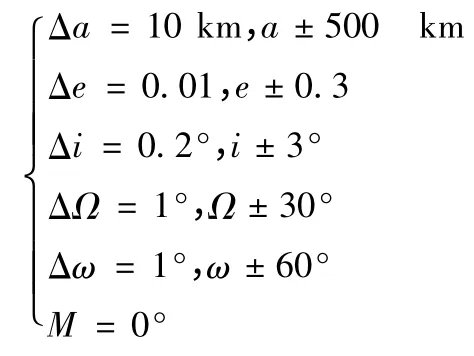
3)在一次步长计算中,应用改进遗传算法进行仿真优化,得到拦截器对各目标累加所需的当前步长最小速度增量
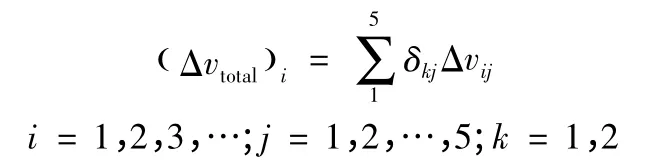
4)在拦截器轨道参数变化值域内进行所有步长的循环计算;
6)得到最终的拦截器停泊轨道数据。
4 仿真分析
下面根据文献[7]中的结论拟合出一组目标轨道数据如表1 所示。
好的拦截器轨道初始值能有效节约搜索时间以及提高优化精度,此处根据多次试验选取停泊轨道参数初始值为:a,e,i,Ω,ω,M=7 000 km,0.1,30°,30°,10°,0°根据不同目标的重要性选定权重系数,有方案1:δ1j=0.1,0.2,0.3,0.2,0.2;方案2:δ2j=0.1,0.1,0.3,0.2,0.3,则仿真结果如表2所示。

表1 目标航天器轨道数据

表2 停泊轨道根数优化结果
所需速度增量结果如表3 所示。

表3 速度增量结果
拦截器停泊轨道及目标飞行器轨道示意图如图3 所示。
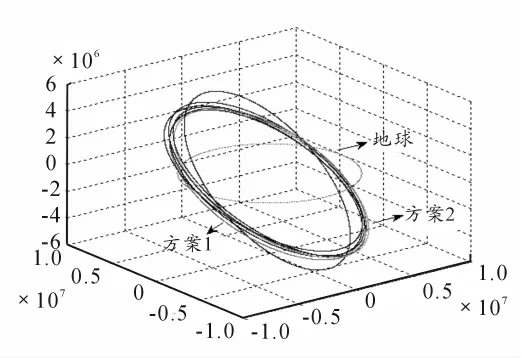
图3 轨道示意图
仿真结果显示,通过优化解算即能够得到一个满足条件的停泊轨道数据优化值,证明了设想的可行性。
5 结束语
从空间作战的角度出发,为优化预备瞄准多个目标航天器的在轨拦截器停泊轨道参数,提出了基于改进遗传算法优化搜索针对多个目标的模型,并设定停泊轨道参数变化值域及步长进行优化解算。最后,通过算例仿真表明,能够有效得到满足设想的停泊优化轨道。为提高我空间国防资源效率做出了一定的基础理论工作。
[1]任萱.人造地球卫星轨道力学[M].长沙:国防科技大学出版社,1988.
[2]袁建平,和兴锁.航天器轨道机动动力学[M].北京:宇航出版社,2010.
[3]云庆夏.进化算法[M].北京:冶金工业出版社,2000.
[4]白洪波,马书兴,朱丽萍,等.空间作战中固定时间轨道拦截的仿真研究[J].航天控制,2006,24(4):62-65/
[5]王石,祝开建,戴金海.用进化算法求解轨道转移的时间——能量优化问题[J]. 宇航学报,2002,23(1): 73-75.
[6]方晓松.卫星轨道建模与仿真技术研究[D].成都:成都电子科技大学,2010.
[7]张云鹤.航天器可达区域分析及摄动影响下相对运动精确轨道控制[D].哈尔滨:哈尔滨工业大学,2010.
[8]秦帅.遗传算法在航天器轨道机动中的应用研究[D].哈尔滨:哈尔滨工业大学,2007.

