金属二维正交切削的有限元分析与刀具角度优化

李玉平 周里群 吴义彬

（湘潭大学机械工程学院湖南湘潭411105）

金属切削过程是一个非常复杂的过程，为了使分析准确和接近实际情况，必须要考虑多方面的因素，综合多学科的知识。实际的金属切削过程都是三维的，但目前对于三维切削的研究还比较困难，许多学者都以直角自由切削为对象将其简化为平面问题，从而对二维的情况进行研究[1-3]。

金属切削过程具有几何非线性、材料非线性、接触和摩擦等，以前主要用试验手段进行研究。随着有限元算法的深入和计算机技术的发展，采用有限元模拟技术对切削过程进行数值仿真成为可能[4，5]。

利用ANSYS有限元软件对切削过程进行分析可分为三个步骤：前处理、计算求解和后处理。前处理包括建立物理模型、选取单元、设定实常数、建立材料模型、划分网格以及建立耦合等；计算求解过程包括设置边界条件、施加载荷、设置求解选项及计算；后处理包括提取数据结果、提取各类云图及制作动画等[6，7]。

选取YT5类硬质合金作为刀具材料，45号钢为工件材料。由金属材料手册[8]可知：YT5类硬质合金的弹性模量为 600 GPa，泊松比为 0.3；45号钢的弹性模量为200 GPa，泊松比为0.28，屈服强度为355 MPa，强度极限为600 MPa，极限变形为 0.16。采用 J.Q.Xie建立的应变硬化和热软化材料模型得到45号钢工件材料的应力应变曲线[9]。以二维正交直角切削为研究对象，对45号钢的切削过程进行分析。

1 建立有限元模型

1.1 切屑分离标准

工件材料撕裂形成切屑的过程在有限单元中表示为节点的连续分离。节点分离涉及到分离标准的问题。通常采用的分离标准有几何标准和物理标准两大类。

几何分离标准是基于刀尖前单元节点的距离，并假定在预定义加工路径上的距离小于某个临界值时，该节点被分成两个，其中一个节点沿前刀面向上移动，另一个节点保留在加工表面上。Usui等人引入几何分离标准[10]。

物理标准是基于刀尖前单元节点的物理量而定义的。当单元中所选定物理量的值超过给定材料的相应物理条件时，即认为单元节点分离。Strenkowski使用了等效塑性应变的分离标准，规定在预定义路径上距刀尖前缘最近节点的等效塑性应变达到临界值时，单元节点分离[11]。研究中典型的标准值在0.4～0.6之间选择。

采用物理标准使金属切削的有限元模拟更接近实际情况。但在实际的有限元模拟中，当刀尖达到应该分离的节点时，该点的物理值并没有达到所给定的物理标准，即切屑在该点并没有分离。因此，为了更好地实现切削加工的仿真，采用基于几何和等效塑性应变的综合标准作为切屑分离标准。该方法以物理标准为主要判断依据，但在刀尖接近分离点并小于给定的几何标准时，可以强迫节点分离。选取0.5为等效塑性应变分离标准值，0.3 L为几何分离标准值，其中L为刀尖前单元的边长[9]。

1.2 定义接触

在金属切削过程中，由于刀具的强度远比工件的强度高，刀具可以被视为弹性体，而工件被视为弹塑性体，故这里将刀具与工件之间的接触定义为刚体对柔体的接触。

在金属切削过程中，刀具前刀面与切屑底层之间的接触、刀具后刀面与已加工表面之间的接触，都可以看作是面对面接触。选用 Targe169作为目标单元，对刀具前后刀面划分单元；选用 Conta172单元，对工件预切削路径上切屑底层和加工表面划分单元。根据实际情况，金属切削过程中只有两个接触对，即前刀面与切屑底层的接触、后刀面与已加工表面的接触。但由于工件选用的VISCO106单元具有较大的变形功能，在模拟计算过程中，切屑底层单元在刀具的挤压作用下变得细长，为防止其渗入到已加工表面层单元中，确保计算能够顺利进行，本研究在切屑底层与已加工表面间定义了第三对接触。该接触也采用面对面接触，其接触类型对计算结果影响不大。

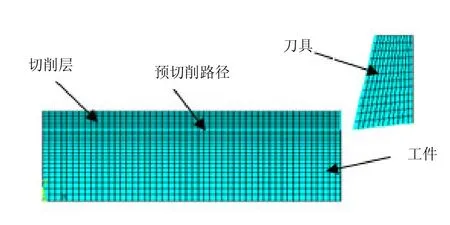
图1 正交自由直角切削有限元模型

对二维正交金属切削过程进行研究，将其视为平面应变问题[1]，建立二维模型，如图1所示。工件模型长25 mm，高10 mm；刀具前角10º，后角8º，刀尖半径为零，将其视为绝对锋利。选取具有大塑性应变功能的VISCO106单元和PLANE182单元分别对工件和刀具的二维实体模型划分网格，并将PLANE182单元的属性设置成平面应变问题。划分网格时采用映射法，工件划分为2 500个单元，刀具划分为144个单元；刀具上各处摩擦因数设为0.7[12]。

1.3 施加约束及载荷

工件底层施加位移全约束，左侧边界限制水平位移；刀具顶层限制竖直方向位移，对右侧边界施加微小位移载荷。刀具的切削过程分多个时步进行，每计算完一个时步之后，保存结果，并在此基础上施加新的位移载荷，重新计算。在每个时步中，严格控制刀具位移量与加载时间的比值，以保证刀具恒速切削。

2 计算结果及分析

2.1 刀具前角对剪切角的影响

刀具前进的方向与剪切面所成的锐角为剪切角。采用不同前角的刀具进行切削过程模拟，并提取网格变形图[9]。将图片导入到AUTOCAD中，通过画出代表刀具前进方向的直线和代表剪切面的直线，可获得剪切角的大小，见表1。从表1中可以看出，当刀具前角增大时，剪切角随之增大，说明第一变形区材料变形减小。

表1还给出了李和谢夫以及麦钱特剪切角理论计算值[1,2]。对比三组数据发现它们的接近比较好。ANSYS计算的剪切角与李和谢夫理论更为接近，说明李和谢夫理论更适合剪切角的计算，也说明了有限元计算的有效性。

2.2 切削速度对刀具受力的影响

采用单因素条件，保持刀具前角 10º，后角 8º，切削厚度2 mm不变，分别以40、80、120、160、200 m/min的切速进行模拟。经过多次仿真，得到在切削稳定状态下，刀具的最大等效应力值，数据见表2。

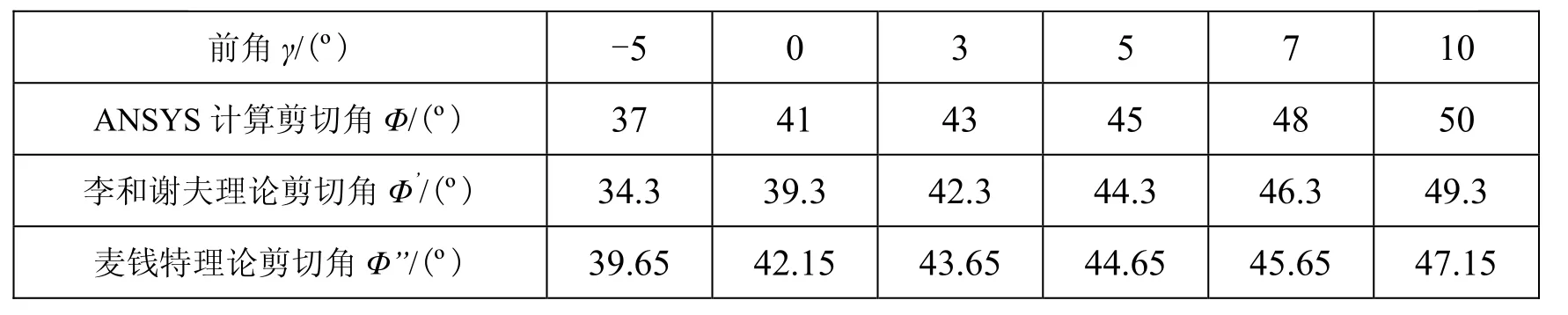
表1 不同前角所对应的剪切角

从表中数据可以看出，随着切削速度的提高，刀具最大等效应力值呈下降趋势。这与试验法所得切削速度与切削力的关系是一致的。这是因为切削速度增大后，剪切角增大，变形系数减小，从而使切削力减小。

表2 不同切削速度下刀具的最大等效应力

2.3 前角对刀具受力的影响

保持后角不变，仍然采用2 mm的切削厚度，切速为 200 m/min。分别以 10º、7º、5º、3º、0º及-5º前角进行模拟。经过计算，得到在切削稳定状态下，刀具的von Mises等效应力云图如图2所示。不同刀具前角的最大等效应力值见表3。

从图2可以看出，不同前角的刀具所承受的等效应力分布情况大体一致，最大应力分布在刀尖位置，靠近后刀面位置承受了较大的应力，且分布面积也较大。表3数据表明：刀具承受的应力值与前角成非线性关系，当 γ=3º时出现最小的应力值，该前角数值可作为刀具前角优化的参考数据。从γ=3º开始，前角增大或减小都会引起刀具应力的增加。前角太小或为负前角时，刀具对切屑的挤压作用较为明显，从而使得切削力较大。

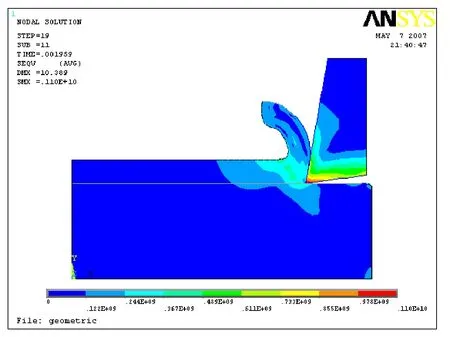
图2 切削过程刀具和工件的等效应力云图（单位：Pa）

表3 不同前角刀具的最大等效应力

2.4 后角对刀具受力的影响

根据上面的分析可知：在单因素条件下，前角为 3º时刀具受力状况最佳。因此保持 3º的刀具前角及其它切削条件不变，只改变刀具的后角，建立不同的模型进行模拟，得到不同后角刀具的最大等效应力值见表4。表4数据表明，刀具所受的应力并非随后角的变化而单调变化，而是在α=5º时出现最小值，此时刀具的受力状况良好，是设计刀具后角和进行刀具参数优化的依据。刀具后角为°3、10º、12º时，等效应力都有大幅增加。一方面后角太大会削弱切削刃的强度，另一方面后角太小会使后刀面迅速磨损，因此，这两种情况都应该避免。

表4 不同后角刀具的最大等效应力

4 结语

以YT5类硬质合金刀具切削45号钢为研究对象，建立了工件材料的应变硬化及热软化模型。利用ANSYS软件，建立了二维正交切削过程的有限元模型，并进行了仿真。提取了一系列数据和云图，对工件材料及刀具等效应力分布状况进行了分析。改变切削用量和刀具参数，进行多次仿真，从结果中提取数据并进行比较，分析了切削用量对刀具受力的影响，并以刀具受力最小为优化目标对刀具参数进行了优化，得到以下结论：YT5类硬质合金刀具切削45号钢，宜采用前角为3º和后角为5º的刀具，刀具在稳定切削状态下的应力最小，抗破损能力最好，磨损最少。

该研究受到湖南省科技厅2012项目资助，在此表示感谢。

[1] Chandrakanth Shet， Xiaomin Deng. Finite element analysis of the orthogonal metal cutting process [J].Journal of Materials Processing Technology， 2000， 105：95－109

[2] C.Shet， X.Deng. Residual stresses and strains in orthogonal metal cutting [J]. International Journal of Machine Tools & Manufacture， 2003，43： 573－587.

[3] 闫洪，夏巨谌.H13淬硬模具钢精车过程的数值模拟[J].中国机械工程，2005，16(11)： 985－989.

[4]黄志刚，柯映林，王立淘.金属切削加工有限元模拟的相关技术研究[J].中国机械工程，2003，14(10)： 846－849.

[5] 谢峰，赵吉文，张崇高，等.剪切角理论研究有限元新方法探索[J].中国机械工程，2003，14(18)：1539－1541.

[6] 王国强.实用工程数值模拟技术及其在ANSYS上的实践[M].西安：西北工业大学出版社，1999.

[7] 谭建国.使用 ANSYS6.0进行有限元分析[M].北京：北京大学出版社， 2002.

[8] 李春胜，黄德彬.金属材料手册[M].北京：化学工业出版社，2004.

[9] 陈志刚，周里群，黄霞春.基于 ANSYS的金属切削过程有限元仿真[J].凿岩机械气动工具，2007(1)： 46－54.

[10] E.Usui， T.Shirakashi. Mechanics of Machining-from Descriptive to Predictive Theory[J]. On The Art of Cutting Metals-75 Years Later， ASME-PED，1982，7： 13－35.

[11] J.S.Strenkowski， J.T.Carrol， A finite element model of orthogonal metal cutting， ASME， Journal of Engineering Industry[J]. 1985， 107(4)： 347－354.

[12] 陈日曜.金属切削原理[M].北京：机械工业出版社，2002.