考虑饱和影响的绕线转子无刷双馈电机性能

程 源 王雪帆 熊 飞 张经纬 阚超豪

（华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074）

1 引言

无刷双馈电机是一种具有广泛应用前景的新型电机，它既可以作电动机运行又可以作发电机运行[1,2]。其定子槽中嵌有两套不同极对数的三相绕组，一套为功率绕组，极对数为p1，另一套为控制绕组，极对数为p2，通常要求|p1−p2|≥2，否则电机会产生较严重的振动；而其转子结构多种多样，主要有磁阻式、特殊笼型和绕线型三种结构[3,4]。无论采用哪种结构，都要求转子能够同时耦合p1对极磁场和p2对极磁场，这样才能使定子两套绕组间实现能量的传递。

无刷双馈电机有着众多的优点：作发电机运行时能够实现变速恒频恒压发电[5]；作电动机运行时其转速只由两套绕组的通电频率决定而与负载无关[6]；与有刷双馈电机相比，去掉了电刷使系统的可靠性大大提高。由于电机本身还存在着若干问题所以至今尚未进入工业化应用阶段，诸如作电动机运行时会产生失步[7]、转子绕组较高的谐波含量使得电机效率不高、还有两套磁场共用一个铁心时的饱和效应等问题。

针对这些问题，国内外研究者对无刷双馈电机进行了广泛而深入的研究，取得了一定的研究成果[8-16]。但是以往的研究绝大多数是基于解析的方法，而解析法的前提就是认为磁路线性不考虑饱和影响，由于无刷双馈电机铁心中存在两套大小相当的磁场，所以铁心饱和对电机性能计算结果产生的影响是不可忽略的[17]。为了能够更加准确地分析无刷双馈电机的性能，本文建立了无刷双馈电机的有限元模型并采用瞬态分析法分析了电机的相关性能。

2 有限元模型

由于无刷双馈电机的转子结构多种多样，对于不同的结构建模方法亦不相同，本文以绕线转子无刷双馈电机为研究对象，模型的的相关参数见表1。

表1 模型参数Tab.1 Parameters of model

图1 给出了无刷双馈电机几何模型的1/4 截面图，其中定子槽中绕组共分三层，槽底部嵌放单层控制绕组，槽口为双层的功率绕组，转子绕组是经过特殊设计的，它利用齿谐波原理同时产生正转的四极磁场和反转的八极磁场以耦合定子上两套极对数不同的绕组。无论定转子绕组是何种连接方式，它们总是由一系列线圈经过串、并联组合而成的，所以在有限元模型中以每一个线圈为研究对象，通过Maxwell 2D 瞬态求解器中的外部电路模块对它们按需要的方式进行连接。这样做不仅可以方便地更改绕组方案，而且在外部电路中可以对电机施加各种形式的激励源和负载从而实现电机的场路耦合计算。

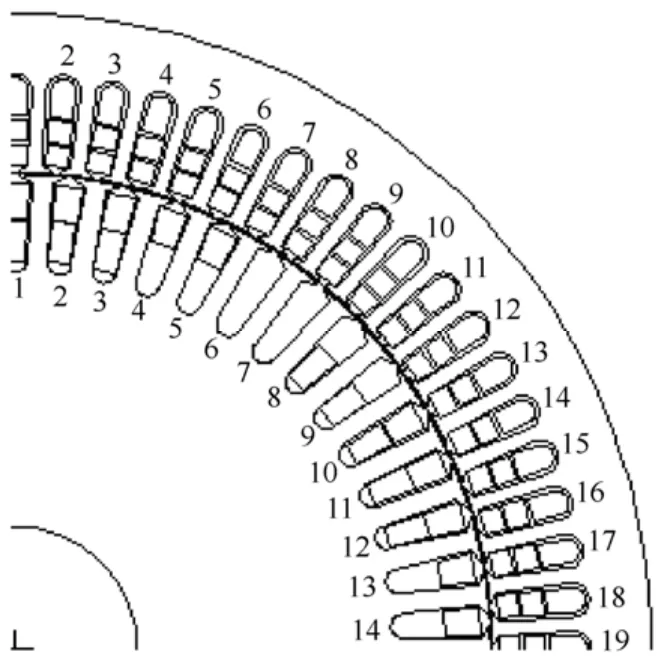
图1 几何模型截面图Fig.1 Sectional view of geometrical model

对于单个线圈需要设置为铰链导体，铰链导体忽略趋肤效应，可看成很细的细段，在实际的有限元网格中不便建模[18]。因而瞬态求解器把其对电流密度的贡献平均到整个问题区域，这些细段串联或并联，通有相同的电流

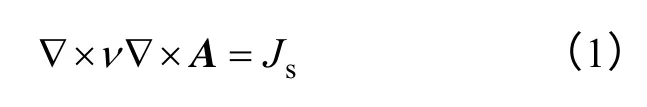
式中ν——运动物体的速度；

A——磁矢量，在无刷双馈电机模型中可以指定定子的外边界为零矢量磁位，这样只对定子以内的区域进行计算；

Js——均匀分布的电流密度，可表述为Js=dfNfif/(Sfap)；

其中，if——流入细段线圈组（绕组）的总电流；

Sf——绕组总的截面积；

a——绕组的并联支路数；

p——原始模型与求解区域的比；

Nf——绕组中导体总数；

df——回路极性（+1 或-1）。

因为在Ansoft的2D 有限元动态仿真中，可以设置物体做平动或转动，并指定其运动速度，所以ν表示的是物体的瞬时速度，在Ansoft 中可以赋予Band 以内的物体具有相同的速度或角速度。

从绕组一端看到的电压是这些导体的总电压与外部电抗电压之和

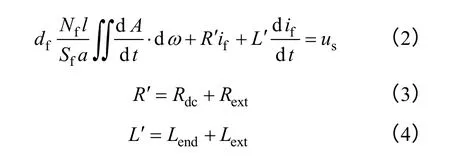
式中Rdc——一相绕组电阻；

Rext——与绕组连接的外部电阻；

Lend——端部漏感；

Lext——与绕组连接的外部电感；

l——电机轴向有效长度。

积分范围为定子外边界以内的所有区域。式（2）中的等式左边第一项在这里主要计算的是无刷双馈电机中相串联导体上的感应电势即反电动势之和。

3 有限元模型的验证

为了对有限元模型计算结果的准确性加以验证，作者将给出常规动态分析法、有限元法各自的计算结果，并将它们和实验结果加以比较。以一台无刷双馈发电机（见图2）为例，其设计参数同表1，原动机采用一台变频调速感应电机（见图2）。控制绕组接变频器，功率绕组接三相负载，负载功率因数为1，作为对发电机运行的要求，无论负载和转速如何变化，始终需要保持功率绕组端的电压（380V）和频率（50Hz）不变，这就需要调节变频器的电压、电流和频率通过改变4 极励磁磁场来实现这一目标。表2 给出不同转速和负载下的控制绕组电压、电流、频率的实测值。

图2 试验样机Fig.2 Experimental prototype

表2 控制绕组电压电流测量值Tab.2 Measured values of voltage and current of control winding

由于 4/8 极无刷双馈电机的自然同步速点为500r/min，所以低于500r/min 时控制绕组的相序同功率绕组的相反，表2 中400r/min 时控制频率为负值即表示反相序。

3.1 常规动态分析法

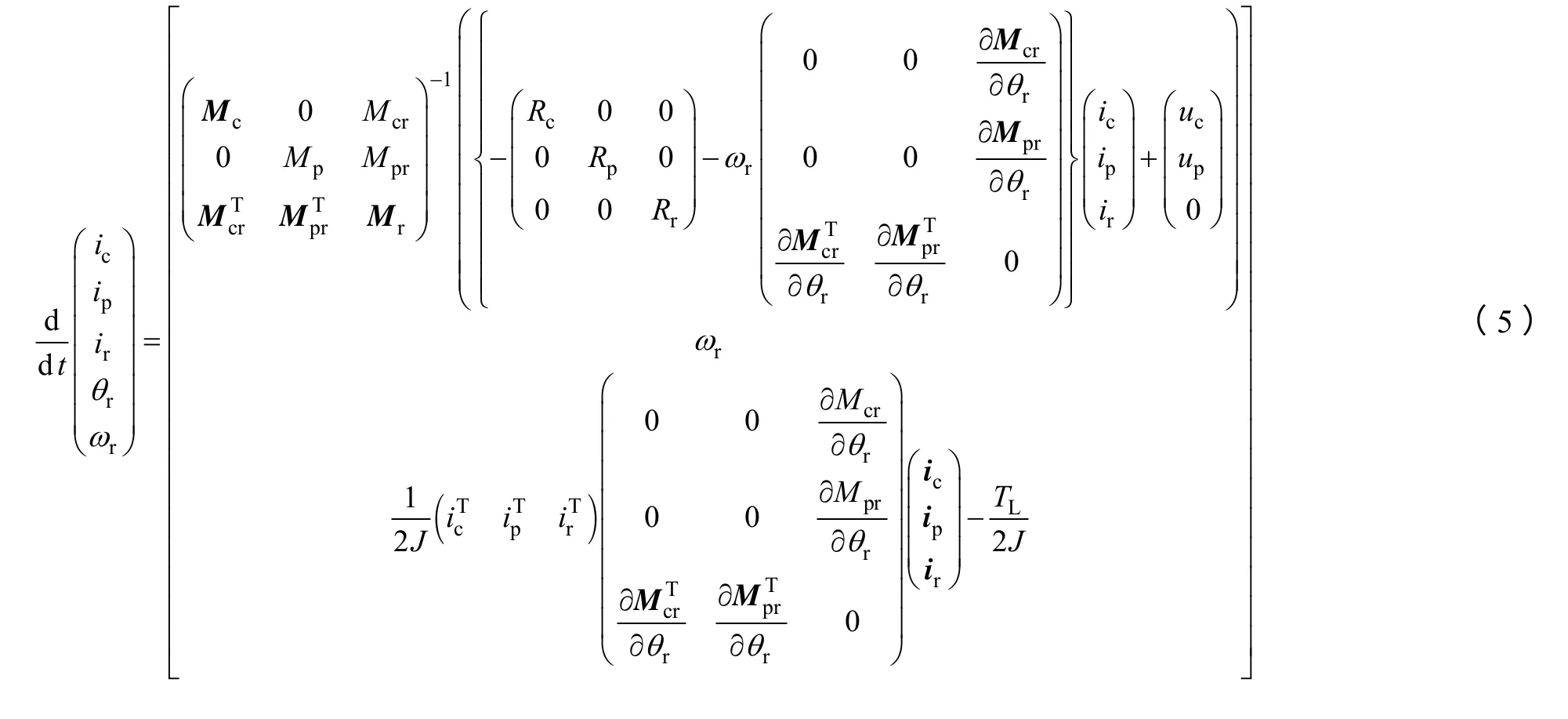
常规的动态分析法主要是基于无刷双馈电机的数学模型以及运动方程，其状态方程如式（5）[19]。

式（5）中Mc，Mp，Mr分别表示控制绕组、功率绕组、转子绕组的自感矩阵；Mcr、Mpr分别表示控制绕组对转子绕组、功率绕组对转子绕组的互感矩阵；θr、ωr均指机械角度和机械角速度。

对该样机而言，其相关参数如下：控制绕组相自感Lcc=88.6mH，相间互感Mcc=−43.3mH；功率绕组相自感Lpp=25mH，相间互感Mpp=−12mH；转子绕组相自感Lrr=603mH，相间互感Mrr=−291.5mH；控制绕组对转子绕组互感幅值Mcr=193mH；功率绕组对转子绕组互感幅值Mpr=60.6mH；电阻Rc=0.113Ω，Rp=0.077Ω，Rr=0.89Ω，转子转动惯量J=8.0kg·m2。做发电机运行时，dθr/(dt)=ωr为常量，dωr/(dt)=0。则由动态分析法计算所得的控制端的电参数见表3。

表3 控制绕组电压电流计算值Tab.3 Calculated values of voltage and current of control winding

对比表2 和表3，在400r/min 和600r/min 空载和负载时的控制电压计算值同实测值的误差在5%以内，而电流计算值同实测值的误差已接近20%，特别在600r/min 带负载时误差达到32.3%，饱和对电机性能计算带来的影响已不可忽略。而在700r/min 时，由于已经靠近八极磁场的同步点750r/min，若想维持功率端电压380V 不变，就必须 增加4 极磁场的强度，这会使得铁心更加饱和，特别在负载时，其电压和电流误差均很大，分别达到20.4%和53.8%。

由于常规动态分析法的前提是假设磁路线性，它无法考虑磁路饱和对电机参数带来的影响。对于无刷双馈电机而言，饱和对电机参数的影响比常规感应电机更大，因为铁心中同时存在两种不同极对数且大小相当的磁场，它们在磁路中相互交叠，任一磁场的变化都会改变磁路的磁阻进而影响到另一套磁场。而且这两套磁场间还存在相对运动，连磁场的分布形态都是时刻变化的，所以利用传统的磁路分析方法对这种饱和效应进行定量分析是非常困难的。

3.2 有限元法

基于以上分析，作者认为有限元法由于其自身的固有特点，它能够考虑到铁磁材料的非线性因素给电机参数带来的影响，不管无刷双馈电机内部磁场是如何分布的，都可以根据每一点的磁场强度并利用该铁磁材料的磁化曲线来计算该点的磁感应强度，所以采用有限元法会得到更加符合实际的计算结果。

以转速在600r/min 时为例，由于控制端的激励源是预先施加的，所以可以通过调整所加电压源的大小并观察功率端的电压来确定最终的控制电压。下面给出电机从空载到负载控制端的电流以及功率端的电压有限元仿真波形。

图3 中给出的电流和电压均为一相绕组的波形，在t=0.523s 从空载突加50kW的纯阻性负载，可以看出，只要及时的增加励磁电流，功率端电压的波动并不很大并很快趋于稳定。由于在[0.4s,0.5s]区间和[0.8s,0.9s]区间电流和电压已稳定，故利用一个周期内的电流电压数据并对其进行平方积分可得到电流和电压的有效值。相关结果见表4。

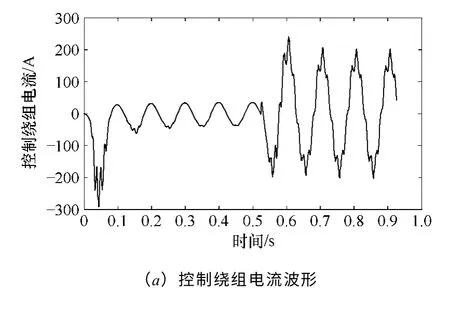
图3 有限元仿真波形Fig.3 Simulation waveform based on finite-element model

表4 控制绕组电压电流有限元计算值Tab.4 Calculated values of voltage and current of control winding based on finite-element model

由于两套绕组均是星形接法，所以控制绕组电流线值等于相值而功率绕组线电压值还需相值乘以1.732。对比表4 和表2 可以看出，无论空载还是负载，电流计算值同实测值的误差均小于5%，而且空载时控制绕组施加的电压为97.2V，负载时控制绕组施加的电压为125V，误差也小于5%，所以有限元计算的结果已能满足工程上的精度要求。使用相同方法分析400r/min 和700r/min的结果可以得出相同的结论。

通过分析图3a 中负载时控制端的电流可以发现电流呈尖顶波，电流中含有较强的三次谐波，说明此时铁心已十分饱和，利用有限元模型，不仅可以计算相关电参数，还可以计算铁心中的磁场分布情况，观察磁路的饱和程度。下面给出对应600r/min 在t=0.926s 时定子齿部和轭部的磁通密度分布图。

图4 中定子齿部磁通密度最大值达到1.81T，而轭部磁通密度最大值达到1.86T，齿部和轭部都已饱和，这是由于该无刷双馈发电机在600r/min 所加负载已超过其原设计负载能力而导致铁心饱和，通过减小负载其齿部和轭部磁通密度值就会下降。图4 仅是某一时刻磁场的分布情况，两套磁场的相对位置改变，其分布形态也会改变，所以传统电机设计中磁路的五段叠加法很难用来分析无刷双馈电机的内部磁场。

图4 定子齿部及轭部磁通密度分布Fig.4 Distribution of magnetic flux density in stator tooth and stator back iron

电机定转子铁心中的磁场分布和磁路饱和情况，也可以通过有限元分析得出的铁心磁通密度分布说明。以无刷双馈电机运行在600r/min 为例，图5 给出的是空载t=0.523s 时电机内部磁场的分布云图，可以看出电机磁场近似成4 极分布，而当电机从空载变为负载运行并稳定后t=0.926s 时的磁场分布如图6 所示，可以看出电机的齿部和轭部磁通密度明显增加。

图5 600r/min 空载时磁场分布Fig.5 Magnetic field distribution of no-load at 600r/min

图6 600r/min 负载时磁场分布Fig.6 Magnetic field distribution of full load at 600r/min

基于上述分析作者认为，采用常规动态分析法若电机饱和程度很低，其计算误差尚在可接受的范围内，若电机带负载时，铁心饱和度较高，就会产生很大的误差，又由于无刷双馈电机磁场分布的不规则性和时变性，传统的磁路分析方法很难对其进行准确的分析，所以只有采用时步有限元法才能对其相关性能进行准确的分析与计算。相关计算结果已经证实了该模型的有效性。接下来利用有限元模型研究功率在定子两套绕组间的分配问题。

4 功率分配

无刷双馈电机最显著的优点就是其控制绕组提供的只是“转差功率”，只占总功率的一小部分，这样就可利用小容量的变频器控制大容量的电机，大大节约了系统的成本，所以，研究功率在定子两套绕组中的分配问题是十分重要的[20]，它是无刷双馈电机的一项重要性能指标。

为了分析无刷双馈电机的功率在两套绕组之间的分配，先设控制端的输入功率为PC，功率端的输入功率为Pp，控制端输入功率在扣除控制端绕组铜耗和对应于控制端极对数磁场的铁耗后由控制绕组传递给转子的电磁功率为PemC，功率端输入功率在扣除功率端绕组铜耗和对应于功率端极对数磁场的铁耗后由功率绕组传递给转子的电磁功率为PemP，消耗在转子绕组中的电功率是由控制绕组和功率绕组同时提供的，所以有以下关系

式中scr——转子同pc对极磁场的转差率，scr=(nc-nr)/nc；

spr——转子同pp对极磁场的转差率，spr=(np-nr)/np。

即转子铜耗由两个磁场的转差功率组成，为了研究PemC和PemP之间的关系，假设转子绕组无铜耗，有

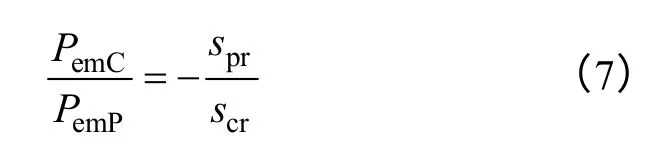
而pp对极磁场在转子中感应电流的频率fpr=sprfp，pc对极磁场在转子中感应电流的频率fcr=scrfc，由于在稳定状态下有[13]fpr=－fcr，所以

式（8）的结论非常重要，可以看出，功率在两套绕组之间的分配近似与频率成正比，在工业应用中，一般都有fp=50Hz，所以越接近自然同步速，它所需的控制电流的频率就越低，即控制端所需提供的功率也就越低。而控制绕组和功率绕组的功率性质（输入或输出）可利用式（7）加以分析。

如果电机运行在高于自然同步速的状态，由于spr=(np-nr)/np，scr=(nc-nr)/nc，所以spr＞0，scr＜0，此时有PemC/PemP＞0，即两套绕组要么同时输入功率，要么同时输出功率，作发电机运行时，就是同时输出功率，作电动机运行，就是同时输入功率。

如果电机运行在低于自然同步速的状态，此时控制绕组反相序，则spr＞0，scr＞0，所以PemC/PemP＜0，所以作发电机运行时，由于功率绕组输出功率，故控制绕组就要输入功率；作电动机运行时，由于功率绕组输入功率，故控制绕组就要输出功率。

以上只是分析了理想状况下功率的分配规律，由于定转子绕组的铜耗以及铁心损耗的存在，实际情形会更为复杂，利用无刷双馈电机的有限元模型，可以计算两套绕组各自的电功率。以转速在600r/min 时的发电机为例，其功率端负载的大小和功率因数是已知的，其功率值易于求取，而控制端的功率因数未知，但通过控制端的电压及电流波形，可以求得其在一个周期内的平均功率。

图7 给出的是600r/min 带负载稳态时发电机控制端一个周期内的电压和电流波形（均为相值），则利用平均功率的定义

可求得控制端的总输出功率为10.101kW，此时功率端总输出功率为50.0kW，符合频率的正比规律，相同方法计算400r/min 和700r/min的结果见表5。

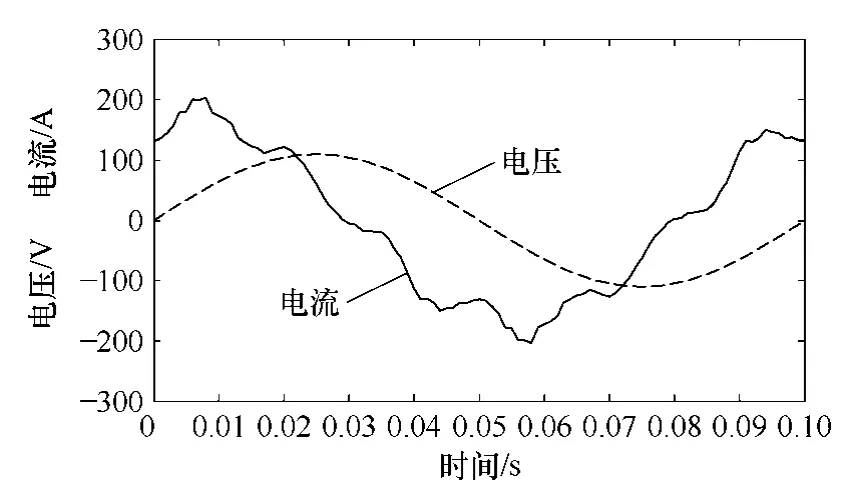
图7 一个周期内电压电流波形Fig.7 Waveform of voltage and current in one cycle

表5 400r/min 和700r/min 时功率分配Tab.5 Power allocation at 400r/min and 700r/min

表5 中负数表示输入功率，由于4/8 极无刷双馈电机的自然同步速为500r/min，故低于自然同步速时，控制端反而要吸收电功率，从表中可以看出，400r/min 和700r/min 时控制端和功率端的功率已经不是严格的正比于通电频率了，而且在700r/min 时控制端与功率端功率已接近相等，这是由于此时很接近八极的同步速点750r/min 时。理论上这一点是发不出电的，越接近这一点其带载能力越低，原因分析如下：该无刷双馈电机样机是以8 极作为功率绕组，4 极作为控制绕组，而且转子是绕线式的，所以该电机是一种感应式的无刷双馈电机。而无刷双馈发电机在运行时是要求功率端的频率保持工频（50Hz）不变的，令功率绕组同步速n1=60f1/p1，控制绕组同步速为n2=60f2/p2，转差s1=(n1-n)/n1，s2=(n2-n)/n2，由于无刷双馈电机转速满足n=60(f1+f2)/(p1+p2)，所以当n=n1时，可以推出60f2/p2=n1，即此时功率绕组对转子的转差和控制绕组对转子的转差均为0，三者保持同步，这样控制绕组4 极磁场无法在转子绕组中感应出电流，转子绕组也就产生不了八极磁场，所以从理论上说，如果感应式无刷双馈电机电机严格在750r/min 运行而无任何偏离，功率绕组就不能发出电来。

但如果是磁阻转子式的无刷双馈电机，它只存在同步性质的转矩，所以在8 极同步速750r/min 运行也是可以发出电的，所以转子结构不同其性质也会有差异。

尽管存在一定误差，但是越靠近自然同步速点，在功率端总输出功率不变的条件下，其控制绕组所需提供的功率越低这一规律是显然的，所以“功率在两套绕组之间的分配近似与频率成正比”只是理论计算上的一种近似，前提是忽略定转子铁耗和转子的铜耗，而作者通过有限元分析其实际的功率分配关系发现，越是接近无刷双馈电机的自然同步速点即500r/min，这种功率分配的正比关系就越接近理论分析的结果，如果电机的运行转速离500r/min这一点越远，由于铁耗和转子铜耗的增加，其控制绕组所须提供的功率就越大于理论分析的结果，这就失去了无刷双馈电机的优势：即降低控制用变频器的容量。故无刷双馈发电机的运行范围应控制在自然同步速附近，不要太过远离自然同步速点，这样才能体现出无刷双馈电机的优势。

5 结论

本文建立了绕线转子无刷双馈电机的有限元模型，采用Maxwell 2D的瞬态分析模块计算了发电机的输出电压和控制电流等相关性能，其计算结果相比传统磁路分析法更接近实测值。讨论了功率在定子两套绕组中的分配关系，指出无刷双馈发电机的运行范围应控制在自然同步速附近，不要太过远离自然同步速点。通过与实验结果的比较，证实了该模型的有效性，它考虑了饱和对电机产生的影响。

[1]McMahon R A,Roberts P C,Wang X,et al.Performance of BDFM as generator and motor[J].IEE Proceedings on Electric Power Applications,2006,153(2):289-299.

[2]McMahon R A,Wang X,Abdi E,et al.The BDFM as a generator in wind turbines[C].The 12th International Power Electronics and Motion Control Conference,2006,1:1859-1865.

[3]王雪帆.一种转子绕组采用变极法设计的新型无刷双馈电机[J].中国电机工程学报,2003,23(6):108-127.Wang Xuefan.A new brushless doubly-fed machine with a wound rotor changing-pole winding[J].Proceedings of the CSEE,2003,23(6):108-127.

[4]熊飞,王雪帆,张经纬,等.绕线转子无刷双馈电机的链型等效电路模型[J].电工技术学报,2010,25(2):15-21.Xiong Fei,Wang Xuefan ,Zhang Jingwei,et al.Chain equivalent circuit model of wound-rotor brushless doubly-fed machine[J].Transactions of China Electrotechnical Society,2010,25(2):15-21.

[5]Brune C S,Spe´e R,Wallace A K.Experimental evaluation of a variable-speed,doubly-fed wind-power generation system[J].IEEE Transactions on Industry Applications,1994,30(3):648-655.

[6]杨向宇,励庆孚.变频器−无刷双馈电机调速系统的仿真研究[J].中国电机工程学报,2002,22(7):95-100.Yang Xiangyu,Li Qingfu.Simulation of inverter-brushless doubly-fed machines for adjustable speed drive systems[J].Proceedings of the CSEE,2002,22(7):95-100.

[7]熊飞,王雪帆,张经纬,等.无刷双馈电机的小信号模型稳定性分析[J].中国电机工程学报,2009,29(33)117-123.Xiong Fei,Wang Xuefan,Zhang Jingwei,et al.Stability analysis of small signal model for brushless doubly-fed machine[J].Proceedings of the CSEE,2009,29(33):117-123.

[8]Williamson S,Ferreira A C,Wallace A K.Generalized theory of the brushless doubly-fed machine—part 1—analysis[J].IEE Proceedings on Electric Power Applications,1997,144(2):111-122.

[9]Williamson S,Ferreira A C.Generalized theory of the brushless doubly-fed machine—part 2—model verifica-tion and performance[J].IEE Proceedings on Electric Power Applications,1997,144(2):123-129.

[10]邓先明,姜建国,方荣惠.笼型转子无刷双馈电机的电磁分析和等效电路[J].电工技术学报,2005,20(8):19-23.Deng Xianming,Jiang Jianguo,Fang Ronghui.The electromagnetic analysis and equivalent circuit of brushless doubly-fed machine with cage rotor[J].Transactions of China Electrotechnical Society,2005,20(8):19-23.

[11]杨顺昌,廖勇,青云.无刷双馈调速电机开环下的性能研究[J].电工技术学报,1999,14(2):27-30.Yang Shunchang,Liao Yong,Qing Yun.Study of steady-state performance of brushless doubly-fed machine for adjustable speed drive under open loop[J].Transactions of China Electrotechnical Society,1999,14(2):27-30.

[12]Wallace A K,Sp´ee R,Alexander G C.The brushless doubly-fed machine:Its advantages,applications and design methods[C].The 6th International Conference on Electrical Machines and Drive,1993,6:511-517.

[13]杨顺昌,徐昌彪.无刷双馈电机的稳态转矩-角特性[J].电工技术学报,1998,13(8):15-18.Yang Shunchang,Xu Changbiao.Steady state torque-angle characteristics of brushless doubly-fed machines[J].Transactions of China Electrotechnical Society,1998,13(8):15-18.

[14]Li R,Spee R,Wallace A K,et al.Synchronous drive performance of brushless doubly-fed motors[J].IEEE Transactions on Industry Applications,1994,30(4):963-970.

[15]Roberts P C,McMahon R A,Tavner P J,et al.Equivalent circuit for the brushless doubly fed machine(BDFM)including parameter estimation and experimental verification[J].IEE Proceedings on Electric Power Applications,2005,152(4):933-942.

[16]Wang F,Zhang F,Xu L.Parameter and performance comparison of doubly-fed brushless machine with cage and reluctance rotors[J].IEEE Transactions on Industry Applications,2002,38(5):1237-1243.

[17]Ferreira A C,Williamson S.Time-stepping finite-element analysis of brushless doubly fed machine taking iron loss and saturationinto account[J].IEEE Transactions on Industry Applications,1999,35(3):583-588.

[18]Williamson S,Lim L H,Smith A C.Transient analysis of cage-induction motors using finite-elements[J].IEEE Transactions on Magnetics,1990,26(3):941-944.

[19]Poberts P C.A study of brushless doubly-fed(induction)machines[D].Cambridge:Univ.Cambridge,2004.

[20]Gorti B,Alexander G,Spée R.Power balance consideration for brushless doubly-fed machines[J].IEEE Transaction on Energy Conversion,1996,11(4):687-692.