非达西渗流效应对低渗透气藏直井产能的影响

张 楠 鲜 波 陈 亮 徐 锋 严仁田 罗 华

（1.中国石油 长城钻探工程有限公司，辽宁 盘锦124010；

2.中国石油 塔里木油田分公司勘探开发部，新疆 库尔勒841000；

3.中国石油 新疆油田公司，新疆 克拉玛依834000；

4.油气藏地质及开发工程国家重点实验室（西南石油大学），成都610500）

国内外大量文献［1－6］表明，低渗透气藏中普遍存在启动压力梯度和应力敏感效应，加之气体渗流过程中本身具有的滑脱效应，使得气体在低渗储层中的渗流规律变得极其复杂，表现出明显的非线性及流态的多变性。戴强等提出启动压力梯度、应力敏感及滑脱效应最终均会引起低渗透气藏渗流的非线性化［7］；刘高波等探讨了启动压力梯度和滑脱效应对低渗透气藏渗流的影响，建立了渗流模型，得到低渗透气藏渗流综合非达西效应随井底流压的变化而变化的结论［8］；杨凯等基于低速达西流动方程，建立了综合考虑启动压力梯度、应力敏感及滑脱效应的修正产能方程，并分析了启动压力梯度、应力敏感对产能的影响［9］。

1 产能方程的推导

目前，在研究介质变形的油气藏渗流理论中，大多采用A.Nur及O.Yilmaz在1985年提出的渗透率模量概念［11］，假设应力敏感系数保持常数

对式（1）积分后，便得到渗透率与压差关系的指数式

式中：α为渗透率模量（应力敏感系数），单位为MPa－1；p为地层压力，单位为 MPa；pi为原始地层压力，单位为 MPa；K 为绝对渗透率，单位为μm2；Ki为原始压力下的绝对渗透率，单位为μm2。

早在1951年，苏联学者B.A.弗洛林就提出了启动压力梯度的概念［12］，目前采用的具有启动压力梯度的渗流公式为

式中：λ为启动压力梯度，单位为MPa／m；v为气体的渗流速度，单位为m／ks；Kg为气体视渗透率，单位为μm2；μ为气体的黏度，单位为mPa·s；r为半径，单位为m。

1941年Klinkenberg利用Warburg的滑脱理论建立了气测渗透率（Kg）与绝对渗透率（K）的关系式［13］

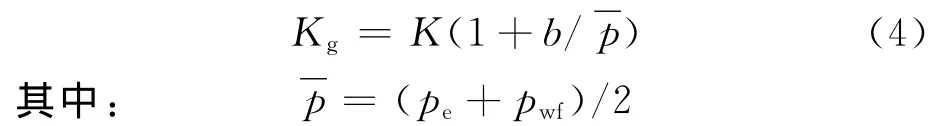
式中：b为滑脱系数，单位为MPa；pe为地层外边界压力，单位为 MPa；pwf为井底流压，单位为为平均地层压力，单位为MPa。

(1) 土体和岩石单元采用Mohr-Coulomb本构，该本构关系满足增量弹性法则和强度准则；将各岩土层分界线设置为水平，其厚度取各岩土层厚度的平均值。

Forcheimer通过实验提出了下面的二次方程来描述高速非达西流动［10］

对于平面径向流，当考虑启动压力、应力敏感和滑脱效应的存在时，联立（2）～（5）式，可得

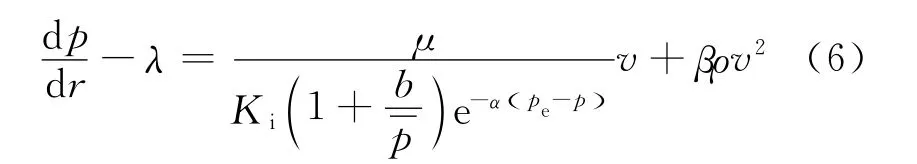
式中：β为非达西渗流系数，单位为pm－1；ρ为气体地层密度，单位为kg／m3。

在稳定流动情况下，可以利用地面产量代替v，同时考虑

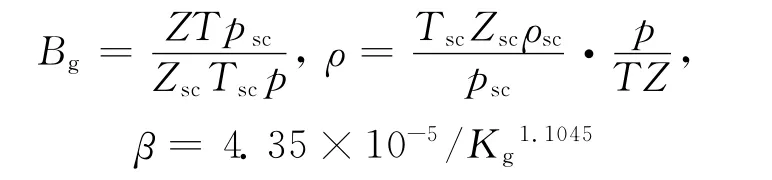
由式（6）可得

式中：ρsc为地面标准气体密度，单位为kg／m3；qsc为地面标准产气量，单位为 m3／ks；Bg为气体体积系数；Z为气体偏差因子；Zsc为地面标准气体偏差因子；T为气体的热力学温度，单位为K；Tsc为地面标准热力学温度，单位为K；psc为地面标准压力，单位为MPa；h为储层有效厚度，单位为m。

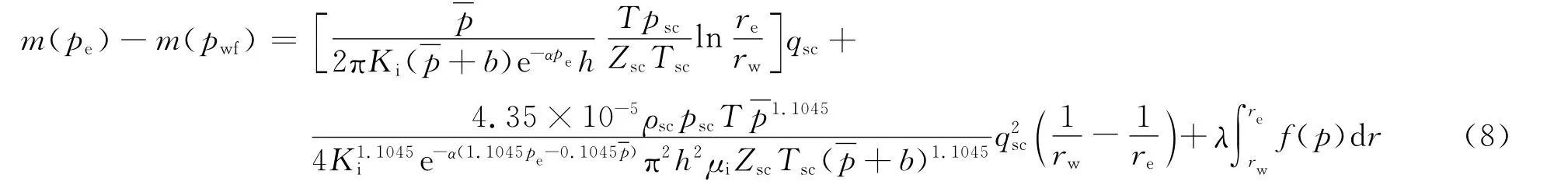
式中：re为泄气半径，单位为m；rw为气井半径，单位为m；μi为原始地层压力下的气体黏度，单位为mPa·s。

假定气藏启动压力梯度λ为常数，则气体流动距离r＝re－rw时的压降为λr，定义λr为启动压力pλ，则

式中dpλ／dp很难求解，可对其作如下简化

式中：Zi为原始地层压力下的气体偏差因子。

由于re≫rw，因此，式（8）可以简化成

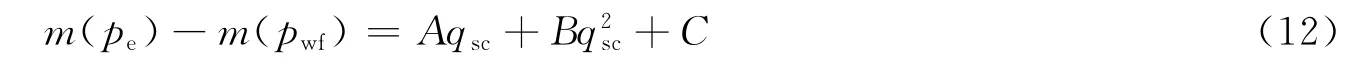
式（12）便是考虑了启动压力梯度、应力敏感和滑脱效应共同影响的低渗透气藏直井产能方程，其中

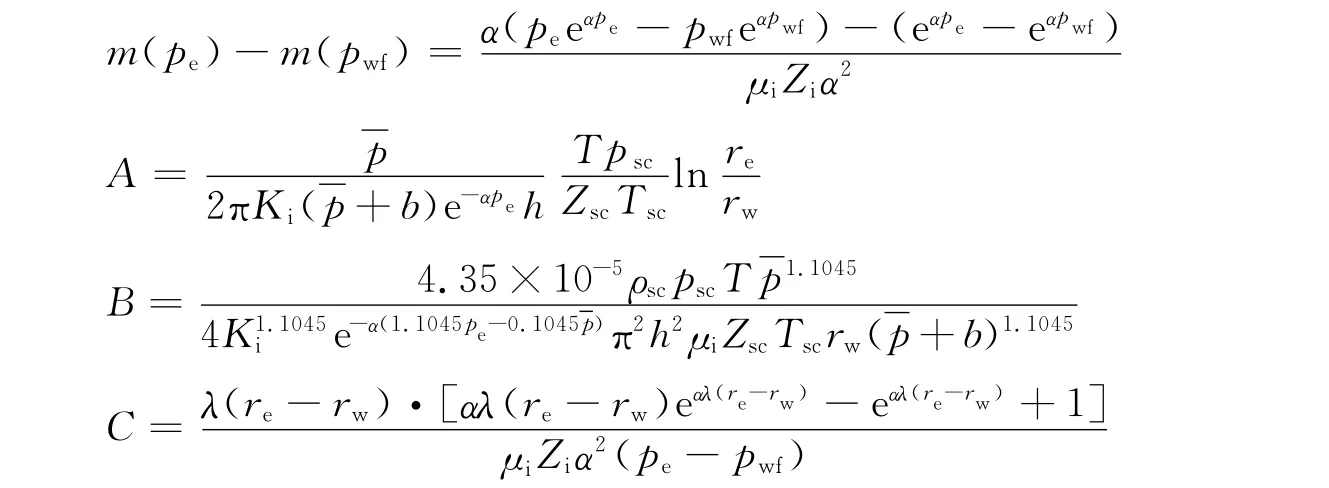
当λ＝0，b＝0时，产能公式就退化为只考虑应力敏感效应时的直井产能方程

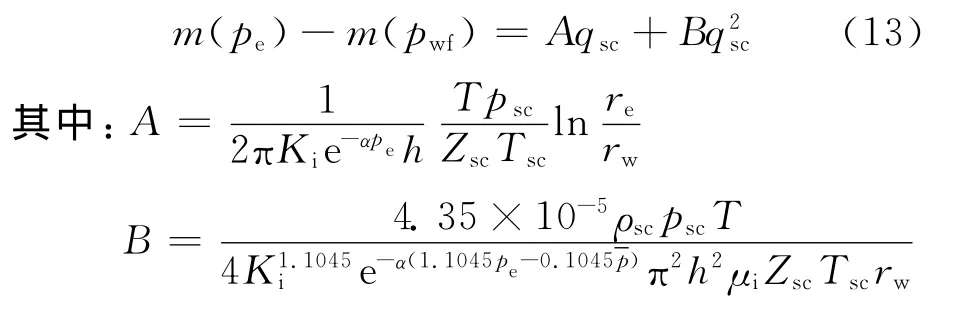
因此当考虑不同因素时，产能方程就会退化为各种不同的形式。

图1 应力敏感效应对直井产能的影响Fig.1 Impact of stress sensitivity on the productivity of a vertical well

2 实例分析

以某低渗透气藏为例，研究启动压力梯度、应力敏感及滑脱效应对低渗透气藏直井产能的影响。计算所需参数如下：pe＝40.86MPa；re＝425.36m；rw＝0.12m；h＝10m；ki＝1.5×10－3μm2；φ＝0.08；T＝393.53K；μi＝0.015mPa·s；Zi＝0.91；启动压力梯度λ 分别取0，0.001，0.002，0.003，0.004，0.005MPa／m；应力敏感系数α分别取0，0.01，0.02，0.03，0.04，0.05 MPa－1；滑脱系数b分别取0，1，2，3，4，5 MPa。计算结果见图1～图6。

a.单独考虑启动压力梯度、应力敏感效应时，气井产量都会降低。但是应力敏感使产量下降的程度更大（图1）。对于指定的应力敏感系数（α＝0.03MPa－1），高流压阶段产气量的降低幅度较小（当pwf＝35MPa时，产量较不考虑应力敏感时仅减少9.04%），低流压阶段产气量的降低幅度较大（当pwf＝17MPa时，产量较不考虑应力敏感时减少30.77%），应力敏感效应使气井产量平均下降幅度为17.71%；而启动压力梯度对气井产量下降的影响较应力敏感小（图2）。对于指定的启动压力梯度（λ＝0.001MPa／m），在高流压阶段，产量降低的幅度相对较大（当pwf＝35MPa时，产量较不考虑启动压力梯度时减少6.69%）；在低流压阶段，产量降低的幅度相对较小（当pwf＝17MPa时，产量较不考虑启动压力梯度时仅减少1.43%）。启动压力梯度使气井产量平均下降幅度为3.09%。

图2 启动压力梯度对直井产能的影响Fig.2 Impact of start－up pressure gradient on the productivity of a vertical well

b.仅考虑气体滑脱效应时（图3），气井产量将会增加。这是因为气体滑脱效应增大了气体视渗透率。对于指定的滑脱系数（b＝1MPa），高流压阶段产气量的增加幅度相对较小（当pwf＝35 MPa时，产量较不考虑滑脱效应时增加2.44%），低流压阶段产气量的增加幅度相对较大（当pwf＝17MPa时，产量较不考虑滑脱效应时增加2.82%）。气体滑脱效应使气井产量平均上升幅度为2.58%左右。

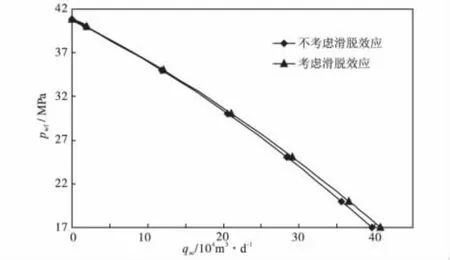
图3 滑脱效应对直井产能的影响Fig.3 Impact of slippage effect on the productivity of a vertical well

图4 不同应力敏感系数对直井产能的影响Fig.4 Impact of different stress sensitivity coefficients on the productivity of a vertical well

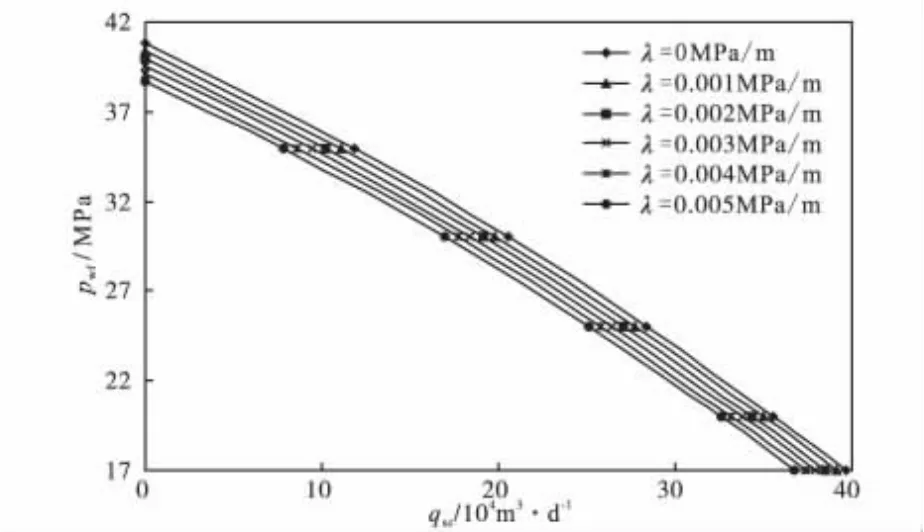
图5 不同启动压力梯度对直井产能的影响Fig.5 Impact of different start－up pressure gradients on the productivity of a vertical well

图6 不同滑脱系数对直井产能的影响Fig.6 Impact of different slippage coefficients on the productivity of a vertical well

c.分析应力敏感效应的敏感性（图4），同一井底流压下，随着应力敏感系数的增加，产气量降低的幅度相应增加。应力敏感系数每增加0.01 MPa－1，气井产气量平均降低6.13%。当应力敏感 系 数 α ＝0.01，0.02，0.03，0.04，0.05 MPa－1时，气井产量（pwf＝17MPa）较不考虑应力敏感分别降低30.77%，36.29%，41.20%，45.57%，49.46%。分析启动压力梯度的敏感性（图5），同一井底流压下，随着启动压力梯度的增加，产气量降低的幅度相应增加。启动压力梯度每增加0.001MPa／m，气井产气量平均降低3.16%。当启动压力梯度λ ＝0.001，0.002，0.003，0.004，0.005MPa／m 时，气井产量（pwf＝17MPa）较不考虑启动压力梯度分别降低1.43%，2.86%，4.31%，5.76%，7.22%。分析滑脱效应的敏感性（图6），同一井底流压下，随着滑脱系数的增加，产气量增加的幅度相应增大。滑脱系数每增加1MPa，气井产气量平均增加2.55%。当滑脱系数b＝1，2，3，4，5MPa时，气井产量（pwf＝17MPa）较不考虑滑脱效应分别增 加 2.82%， 5.62%， 8.39%， 11.13%，13.85%。

3 结论

a.针对低渗透气藏的非达西渗流特征，建立了考虑气体启动压力梯度、应力敏感及滑脱效应共同影响下的直井稳态产能方程，能更加全面准确地对低渗透气藏进行产能评价。

b.分析了启动压力梯度、应力敏感及滑脱效应各因素对气井产能的影响程度。得出应力敏感效应对产能的影响最大，但是气体滑脱效应与启动压力梯度的影响也不能忽略，这主要是由于气体黏度远比油小。

c.在本文实例中，应力敏感效应使气井产量大幅下降，最大可下降49.46%；启动压力梯度使气井产量小幅下降，平均下降幅度为3.09%；气体滑脱效应使气井产量小幅上升，平均上升幅度为2.58%。

d.建议在低渗透气藏开发中应充分考虑应力敏感效应的影响。

［1］郭肖，伍勇.启动压力梯度和应力敏感效应对低渗透气藏水平井产能的影响［J］.石油与天然气地质，2007，28（4）：539－543.

［2］汪周华，钟兵，伊向艺，等.低渗气藏考虑非线性渗流特征的稳态产能方程［J］.天然气工业，2008，28（8）：81－83.

［3］刘晓旭，钟兵，胡勇，等.低渗透气藏气体渗流机理实验［J］.天然气工业，2008，28（4）：130－132.

［4］宋传真，郑荣臣.致密低渗气藏储层压力敏感性及其对单井产能的影响［J］.大庆石油地质与开发，2006，25（6）：47－49.

［5］王昔彬，刘传喜，郑荣臣.大牛地致密低渗透气藏启动压力梯度及应用［J］.石油与天然气地质，2005，26（5）：698－702.

［6］朱光亚，刘先贵，李树铁，等.低渗气藏气体渗流滑脱效应影响研究［J］.天然气工业，2007，27（5）：44－47.

［7］戴强，段永刚，陈伟，等.低渗透气藏渗流研究现状［J］.特种油气藏，2007，14（1）：11－14.

［8］刘高波，刘荣和，冯文光，等.低渗透气藏非达西渗流渗流研究［J］.大庆石油地质与开发，2007，26（1）：65－67.

［9］杨凯，郭肖，肖喜庆，等.修正的低渗透气藏产能方程［J］.天然气工业，2009，29（4）：68－70.

［10］Forchheimer P H.Wasserbewegung durch boden［J］.Z Ver Deutsch Ing，1901，45：1781－1788.

［11］Nur A，Yilmaz O.Pore pressure fronts in Fractured Rock systems［D］.Stanford：Department of Geophysics，Stanford University，1985.

［12］戈尔布诺夫.异常油田开发［M］.北京：石油工业出版社，1987.

［13］Klinkenberg L J.The permeability of porous media to liquids and gases［J］.API Drilling and Production Practice，1941（2）：200－213.