电力系统电压稳定控制方法的发展与应用

李 楠，谢海英，张天舒

(1．辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006;2．东北电力第三工程公司，辽宁 锦州 121001;3．金山能源有限公司，辽宁 沈阳 110006)

随着科技进步和经济的不断发展，电力负荷和电网容量迅速增加，电力工业向“大系统、超高压、远距离、大容量”发展。但随之而来的电压稳定问题愈加明显，引起业界广泛关注。近几十年来，世界各地发生了许多由于电力系统失稳导致的电力系统大面积停电事故，不仅造成巨大的经济损失，而且影响社会稳定。因此电压稳定性分析是电力系统运行面临的重要而复杂的任务。

1 电力系统电压稳定理论研究方法

电压稳定问题研究方法主要是基于潮流方程的静态电压稳定分析方法和基于状态方程的动态电压稳定分析方法。静态电压稳定分析方法是基于潮流或扩展潮流方程的分析方法，动态电压稳定分析方法是建立在微分代数方程 (DAE)的基础上。电压稳定基于静态的分析方法较为成熟，而且应用广泛，但随着研究的不断深入，电压稳定问题逐渐被认定为本质上是一个动态稳定问题。由于动态负荷模型众多，各种模型仿真对电压稳定的影响结果各不相同，关于动态电压稳定理论与静态电压稳定的研究相比仍然不够完善。

1.1 静态分析方法

静态安全指标分为运行点的状态指标和基于过程的裕度指标。运行点的状态指标反映了系统邻近崩溃点的某些特征，通过计算当前运行点的相应量间接评价系统当前运行状态与稳定极限的邻近程度。基于过程的裕度指标是通过当前电压稳定运行点与稳定极限点的差值，判断当前状态与失稳状态的直接距离。主要方法包括潮流多解法、奇异值分解、特征值分析法、模式分析法、连续潮流拓展法、最大功率法和灵敏度法等。

利用潮流多解法计算静态安全状态指标可以判断系统电压稳定状态。潮流方程为一个非线性方程，可能存在多个实数潮流解，随着负荷的不断增加，其潮流解的对数越来越少，最后只剩下一对潮流解，高电压解和低电压解。高电压解和低电压解均值正好是系统电压稳定临界点处的电压值，低电压解被证明为不稳定解。系统电压稳定状态可通过计算高电压解与低电压解的距离判断，但该方法对低电压解很难求取。灵敏度法是通过计算在某种扰动下，采用系统变量对扰动的灵敏度来判断系统的稳定性。潮流方程表示为［1］

式中 α——参数变量;

X——状态变量;

U——控制变量;

Y——输出变量。

根据不同灵敏度，利用基本方程对控制变量U、参数变量α求全微分:

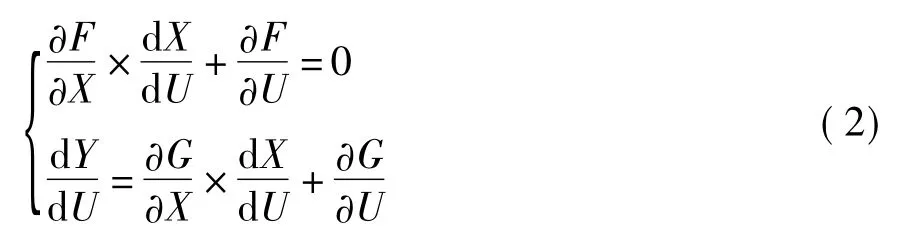
将式 (3)在平衡点X0处泰勒展开略去高阶项得:ΔZ=Fx×ΔX=JRΔX，对JR进行奇异值分解，设 JR非奇异，得:VTJRU=diag(δ1，δ2，……，δn)，代入泰勒公式得:ΔX=U×Λ－1×VT得:由于最小奇异值在F范数意义上反映了矩阵至矩阵奇异之间的最短距离，因此，利用矩阵最小奇异值可以表示当前系统与静态稳定极限之间的最短距离。但雅可比矩阵的非线性，不易提供对系统稳定裕度的预测。最大功率法是基于网络能够传送功率的极限而求取电压稳定的方法，当负荷需求超过网络所能传输的功率极限时，将这一临界运行状态称为电压稳定极限运行状态，求临界点是该方法的关键。连续潮流法是解决临界点的求取方法，通过引入一维校正方程，消除了潮流雅可比矩阵奇异现象，使该方法得到广泛应用。由于获取临界点需要的计算量很大，计算速度较慢，不适于在线应用。

静态研究方法在获取电网极限运行状态、指导生产调度等方面发挥了重要作用，为动态分析方法的研究奠定了基础。

1.2 动态分析方法

随着研究的不断深入，电压稳定问题的动态本质引起了人们的重视，人们逐渐认识到要从根本上解释电压失稳机理必须建立电力系统的动态模型，用各种动态分析方法来研究电压崩溃现象的物理本质，目前电压稳定性分析的动态方法主要有小干扰分析法、时域仿真法、动态潮流法等。

少扰动分析法主要步骤是根据研究对象考虑恰当的动态元件，建立描述系统动态过程的模型，列出系统微分—代数方程 (DAE)，在平衡点将DAE线性化，消去方程中的非状态变量，得到线性化微分方程，然后根据线性化微分方程雅可比矩阵特征值的实部判断系统的稳定性。但小扰动稳定分析方法计算量较大，实际的电力系统稳定分析中较多采用静态方法。当系统遭受大扰动时必须采用时域仿真法对电压稳定性进行研究。时域仿真法采用数值分析方法进行研究，得到电压及一些变量随时间变化曲线，该方法具有较高的建模精度和分析结果。

暂态电压稳定分析可分为时域仿真法、李雅普诺夫直接法及扩展等面积准则。但时域仿真速度较慢，李雅普诺夫直接法需要积分到扰动消失，在工程应用中受到一定限制。扩展等面积准则采用灵敏度分析技术，避免了大量的积分试探而直接估计极限值，提高了仿真过程的计算速度。当电压失稳过程持续很长时间时，必须进行中长期电压稳定研究。针对长期电压稳定特点，Dr．Van Cutsem提出快速时域仿真法QSS。QSS仿真算法认为在长期电压不稳定的情况下，发电机及其调节器的动态响应为瞬时响应，平衡方程代替了发电机及调节器的动态方程，其模型由电压稳定分析的系统多时标方程演化而来。

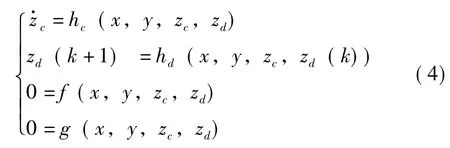
式中 x——发电机和调节器的状态向量;

y——网络节点电压向量;

zc——与负荷动态相关的连续状态向量;

zd——OLTC的变比等离散变量。

QSS仿真求解步骤是寻找长期动态发展过程中的一系列暂态平衡点，在每个时间步长上暂态平衡点的求取就是快动态变量x、y对慢动态变量zc、zd变化做出响应。QSS仿真算法能反映控制作用和元件动作的时域规律，计算速度快、收敛性好。文献［2］提出将直接法应用于带参数的QSS仿真系统模型中，解决系统极限求取中QSS方程在崩溃点附近存在病态问题。

1.3 静态分析与动态分析的关系

数学上的分岔理论研究非线性系统在参数变化下是否能保持原来系统稳定性的问题，而静态电压稳定问题可视为系统在不同负荷水平下发生分岔的问题。分岔理论建立了系统分岔与系统稳定性的关系。静态电压稳定临界点与动态分析下的SN分岔点是一致的，在这一基础上，静态分析方法可有一动态的解释。

高阶电力系统动态特性可用与系统参数有关的非线性微分—代数方程组描述［3］:

式中 f——代表系统;

g——潮流方程;

X——系统状态变量;

Y——除状态变量以外的其他变量;

p——系统参数和操作参数。

对于每一组确定的系统参数p，系统平衡点X*是式 (5)的解。小扰动线性化形式为

对于系统的结构性稳定问题，雅可比矩阵特征值的实部决定系统在某个平衡点的稳定性，出现正实部则系统不稳定。鞍结分岔Hopf分岔所隐含的假设为gy不奇异。如果参数逐渐变化到gy奇异时，雅可比矩阵的特征值改变符号。当特征值由－∞→+∞，表现为单调失稳，系统发生奇异诱导分叉，此时小扰动方程式无解［1］。提出暂态稳定分析方法，可通过引入一个很小的正常数ε，利用奇异扰动方法处理代数方程，得到奇异扰动形式的微分方程模型:X·=f(X，Y，P)，εY·=g(X，Y，P)，原DAE的奇异点将消失。

2 电力系统电压稳定的控制

电压稳定控制按类型可分为紧急控制和预防控制。根据电压静态稳定分析理论和电网运行的经济角度，电力系统稳定运行时，应保持一定的电压稳定裕度，对电力系统电压稳定进行预防控制。通过改变网络参数、增加系统所需无功容量等方式，使运行状态远离电压稳定的临界状态，保持电压质量稳定。当线路及变压器传输功率时，由 ΔU=可知，传输无功功率将引起电压降落，需要改变网络参数，串联电容及无功补偿设备，抵消部分电抗，达到保持电压稳定的作用。当系统发生小扰动而进入弱稳或不安全区域时，通过无功功率控制或减轻系统负荷的方式使系统进入稳定区域。

在电力系统出现故障等特殊的情况下，电压稳定裕度不足甚至趋于电压崩溃时，如何通过各控制器的协调动作，最大限量地确保负荷供电，为恢复创造良好条件是目前重要研究课题。目前常用的方法主要有改变系统潮流、投入无功补偿装置、改变有载调压变压器 (OLTC)的电压设定点、甚至切除部分负荷，保证电压的稳定性。当系统中局部节点负荷变化较大时，需要适时调整无功电源保持电网电压稳定。在电网中无功电源主要由发电机及无功补偿装置组成，无功补偿装置包括投切并联电容器、调相机、SVC、SVG装置。发电机不仅是有功电源，也是无功电源，可以通过发电机的自动励磁调节设备自动调整发电机的机端电压、分配无功功率。对于发电机直接供电的负荷，如果线路不长、电压损耗不大，可以直接通过发电机调压就能满足负荷电压要求。如果通过多级变压供电，需照顾距离发电机近处的负荷，电压不能调的过高，远处的负荷还要靠有载调压变压器等措施解决。依靠OLTC控制电压质量在某种情况下不利于电压稳定，OLTC和发电机过励限制等慢动态装置相互作用可能引起电压失稳。如果系统发生罕见的严重复杂故障，导致系统趋于电压崩溃，如果不能保持系统稳定运行，则必须有选择地切除部分负荷，防止系统崩溃［4］。由于电网系统故障的复杂性，当电网濒于崩溃时，为做出快速准确判断切除负荷达到电网稳定的目的，很多地方已将大停电防御体系应用到实践中，并取得了积极的效果。

3 结束语

目前，对电力系统电压稳定分析的研究仍主要集中在动态分析方法及电压崩溃机理的研究，预防电压崩溃的发生、确定合适的无功储备和稳定裕度、校验紧急控制策略的优劣、在线生成控制策略、确定保护系统的协调动作等仍有待进一步研究。

［1］ 周双喜，朱凌志，郭锡玖，等．电力系统电压稳定性及其控制［M］．北京:中国电力出版社，2004．

［2］ 安 宁，陈兴雷，任 瑞，等．基于准稳态分析求取中长期电压稳定极限新方法［J］．电力系统保护与控制，2011，39(18):1－7．

［3］ 王庆红，周双喜．电力系统微分代数模型奇异诱导分岔分析［J］．中国电机工程学报，2003，23(7):18－22．

［4］ 程浩忠，吴 浩．电力系统无功稳定性［M］．北京:中国电力出版社，2004．

［5］ 袁季修．电力系统安全稳定控制［M］．北京:中国电力出版社，1996．

［6］ 段献忠，袁 骏，何仰赞，等．电力系统电压稳定灵敏度分析方法［J］．电力系统自动化，1997，21(4):9－12．