基于分形理论的混凝土大坝结冰变径模型设想

杨 帆，谢明宇

(1．辽宁建筑职业技术学院，辽宁 辽阳 111000;2．辽阳供电公司，辽宁 辽阳 111000)

很多地区水电站大坝深受混凝土抗冻性差问题的困扰。例如云峰水电站，在大坝建成并投入运行的几年里，溢流坝表面混凝土冻融破坏面积高达1 000 m2，占整个溢流坝面积50%左右，混凝土平均冻融剥蚀深度达10 cm以上。大型混凝土结构工程的抗冻性分析往往建立在大量实验数据基础上，若能利用理论达到预测目的，并判断出孔隙水瞬间结冰孔径范围，则可以人为调节孔径大小，提高混凝土大坝等大型混凝土结构工程抗冻能力。

混凝土内部孔隙结构通常是不规则、无序分布、千奇百怪的，不像传统假设那样光滑、平直、等大、规则，材料孔形、面积、体积等在各个尺度上均表现出分形特征。在以往的水泥混凝土材料研究中，渗透性孔隙模型多假设为平滑圆柱孔，而且是直线型的，但实际上孔隙是弯曲、复杂的非平滑表面。为描述其弯曲复杂程度，国外已有学者采用4次Koch曲线模型评价孔隙特征，并通过试验确定了相似维数，使评价更科学合理［1］。

本文将混凝土大坝看作是具有分形结构的空间载体，研究其内部孔隙分形特征，分析孔隙复杂程度及对混凝土大坝结构孔隙水过冷度的影响。同时引入分形理论，根据混凝土材料内部孔隙结构特征，从讨论单位横截面积A0上孔隙直径r分布入手，引入孔隙分布分形维数D以及孔隙通道弯曲分形维数Dτ，得出有关分形孔隙孔隙水过冷度的公式。

1 混凝土冻融破坏机理

混凝土在冻融过程中，遭受的破坏应力主要由两部分组成。其一，混凝土中毛细孔水在某负温下发生物态变化，由水转变成冰，体积膨胀9%，因受毛细孔壁约束形成膨胀压力，在孔周围微观结构中产生拉应力;其二，当毛细孔水结成冰时，由凝胶孔中过冷水在混凝土微观结构中迁移和重分布引起渗管压。由于表面张力作用，混凝土毛细孔隙中水的冰点随着孔径减小而降低。当胶凝孔水形成的冰核温度在－78℃以下时，由冰与过冷水饱和蒸汽压差和过冷水之间盐分浓度差引起水分迁移而形成渗透压。另外胶凝不断增大，形成更大的膨胀压力，当混凝土受冻时，这两种压力会损伤混凝土内部微观结构，经过反复冻融循环以后，损伤逐步积累、不断扩大，发展成互相连通的裂缝，使混凝土强度逐步降低至完全丧失，混凝土表面开始剥落甚至整体破坏。

2 变径理论

2.1 变径理论的提出设想

混凝土材料受冻融破坏主要是由孔隙中水结冰所致。水结冰时体积增大约9%，若混凝土材料孔隙中充满水，则结冰膨胀对孔壁产生很大应力，当此应力超过材料抗拉强度时，孔壁局部开裂。随着冻融次数增多，材料破坏加重。

混凝土材料抗冻性取决于孔隙率、孔隙特征及充水程度。若孔隙不充满水，即远未达到饱和，具有足够自由空间，即使受冻也不致产生很大冻胀应力。极细的孔隙，虽可充满水，但因孔壁对水吸附力极大，吸附在孔壁上的水冰点很低，在一般负温下不会结冰;粗大孔隙一般水分不会充满其中，对冻胀破坏可起缓冲作用;闭口孔隙水分不能渗入;毛细管孔隙既易充满水分，又能结冻，故对材料冰冻破坏作用影响最大。

当温度降至冰点以下时，由于混凝土中水分大部分已结冰，水泥颗粒不能与冰发生化学反应，混凝土强度停止发展，孔隙内水分结冰会引起膨胀(水结冻体积可膨胀约9%)，作用在孔隙毛细管内壁，破坏混凝土内部结构，已经获得强度 (在结冰前混凝土已不同程度硬化)受到损失。当气温忽高忽低反复冻融，混凝土内部微裂逐渐增长、扩大，强度逐渐降低，表面出现剥落，甚至完全崩溃。

混凝土内部结冰从微观上分析是一个类似随机过程，并不是所有孔隙中水在零下时候都结冰。如图1所示。

图1 孔径水结冰

饱和硬化水泥浆中蒸发水由于溶解氢氧化物的原因，不会在0℃时冻结，而冻结一旦开始，纯冰从溶液中析出，溶液浓度提高，冰点进一步下降，在不掺盐类的水泥浆体中自由水冰点约为－1.5～－1℃。由于孔隙表面张力的作用，不同孔径孔内水饱和蒸气压与冰点不同，孔径越小，孔内水饱和蒸气压越小，冰点越低。当环境温度降低到－1.9～－1℃时，混凝土孔隙中水由大孔开始结冰，并逐渐扩展到小孔。一般温度在－12℃时，毛细孔都能结冰，而凝胶孔中水分子物理吸附于水化水泥浆固体表面，在－78℃以上不会结冰。因此在某一固定负温下水泥石中水分只有一部分是可冻水。有些孔隙中过冷水到－78℃才会冻结，且为一个瞬间过程，是瞬时反应。过冷水通过孔隙时结冰与否由孔径决定，孔径大小是能否瞬间结冻的关键。若是可以运用理论分析判断出孔隙水瞬间结冰孔径范围，则可以人工调节孔径大小，提高混凝土材料抗冻能力。

孔隙水是否会结冰是个十分复杂的问题。负温条件下，过冷水通过饱和硬化水泥浆内部孔隙时，可能会因为孔径变化而突然结冰，也可能并未对过冷水过冷度产生影响。

根据研究，引用分形理论研究混凝土内部孔隙结构图可描述出孔隙特征，见图2。

图2 分形孔隙孔径水结冰模型

2.2 具有分形结构的混凝土孔隙结冰

2.2.1 分形

分形学 (Fractal)是由Mandelbrot于1976年首次提出来的。分形的原意是“不规则的、分散的、支离破碎的”物体。

分形理论所研究对象主要是复杂、不规则、具有自相似性的几何形体。分形结构几何体具有以下性质［2］:

a． 具有精细结构，即在任意小尺度下都具有复杂结构;

b． 具有不规则性，整体与局部不能用传统几何语言来描述;

c． 具有自相似形式，可是近似的或统计意义的;

d． 通常分形图形在某种意义下维数大于其拓扑维数;

e． 在大多数情况下，分形图形可用非常简单的方法产生。

分形图形的最基本特征是自相似性和标度不变性。所谓自相似性是指某种结构或过程特征从不同空间或时间尺度来看都是相似的，或者某系统或结构局部性质或局部结构与整体类似。标度不变性是指，从分形图形上任选一个局部区域，无论放大或缩小，它的形态、复杂程度、不规则性等各种特性均不会发生变化，所以标度不变性又可称为伸缩对称性。表征这2种分形性质的定量参数为分形维数(Fractal Dimension)，用来描述一个复杂系统的复杂、不规则程度，为整数或非整数都可，并有多种定义和测定方法。

2.2.2 混凝土孔隙分布分形维数

研究影响混凝土渗透性的介观孔隙通道 (即没有分支的通道，它与孔网格中2个近邻位相连接，孔隙通道两端可都开口，也可一端开口，一端封闭)，其轴线为弯曲、复杂曲线，具有分形特征。

混凝土孔隙分布同样具有分形特征，假定孔隙分形分布在空间基本均匀。图3是正方形单位截面A0上孔隙直径为r的孔隙面积分布。

根据分形基础理论，分形孔隙直径大于r时累积数目N(r)与孔径有如下关系:

式中，r为孔隙直径，cm;D为孔隙分布的分形维数，参考长度L∈ ［rmin，rmax］，rmin、rmax分别为单位截面上最小、最大孔隙直径，cm。

对式 (1)进行r微分可得:

式中，表示直径在 r和 r+dr之间的孔隙数目－dN＞0。

2.2.3 混凝土孔隙通道屈曲分形维数

混凝土孔隙通道形状是弯曲的，孔隙轴线是具有分形性质的复杂曲线。如图4所示，孔隙通道轴线分别为直线、科赫曲线和无规分形曲线。引入孔隙路径的屈曲分形维数Dτ衡量孔隙通道弯曲复杂度。图4中，直线Dτ=1，科赫曲线Dτ=1.261 8，无规分形曲线Dτ＞1。

Yu［3］提出了毛细管长度和直径之间指数关系，可以用于分析混凝土连通孔:

式中:Lτ(r)为孔隙直径为r的孔隙通道长度，cm;Dτ为孔隙通道屈曲分形维数;L0为孔隙通道外观长度，cm。

1≤Dτ＜2，当 Dτ=1时，孔隙通道为直线，此时 Lτ(r) =L0。

孔隙直径在r和r+dr之间的孔隙体积微元dVp为

式中，Lτ(r)为孔隙直径为r的孔隙通道长度，cm。

结合式 (3)和式 (4)得到:

微分得到混凝土孔隙体积为

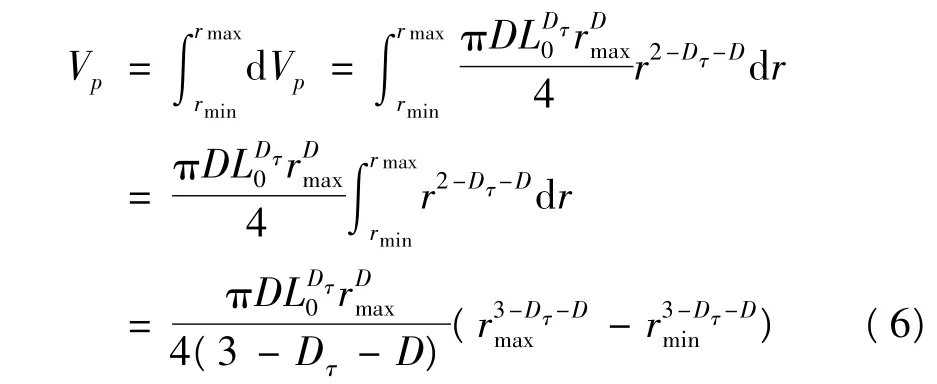
稻叶英男［4－6］通过大量实验，对静止情况下影响过冷水过冷度的因素进行了研究。斋藤认为，在外界条件一定时，发生结冰不是一个确定事件，可用概率描述发生结冰与过冷度之间关系。

在对大量实验进行分析后，得到了过冷度与体积关系为

式中，ΔTm为过冷度，K;V为体积，cm3。

利用分形模型模拟混凝土材料孔隙特征，得到评价孔径与孔隙水过冷度间关系，对研究如何提高混凝土材料抗冻性有很好指导意义。

通过研究模拟结果和积累实验数据，得到过冷度与孔径范围的关系，可人为控制混凝土孔径大小，从而提高混凝土抗冻性和耐久性，具有很好的经济意义。

3 结论

a． 混凝土结冰从微观上分析是一个类似随机的过程，并不是所有孔隙中水在零下时候都结冰，有些孔隙中过冷水到－78℃才会冻结。孔隙中水结冰是个瞬间过程，是瞬时反应，在多大孔径内瞬间结冰是关键。

b． 混凝土材料内部孔隙结冰过程:凝胶孔→变径水 (过冷水)→瞬间结冰。零下状态下，由于混凝土材料内部孔隙孔径、结冰与否、过冷水过冷度不同。有些过冷水过冷度较大，造成冻害大，损害混凝土构件;而有些过冷水过冷度较小，不会冻结和进一步冻害混凝土材料。

c． 引用分形理论模拟混凝土材料内部孔隙特征，提出变径理论，建立假想模型，为进一步提高混凝土抗冻性作出理论铺垫。

［1］ 唐 明，王甲春，李连君．压汞测孔评价混凝土材料孔隙分形特征的研究［J］．沈阳建筑工程学院学报，2001，17(4):272－275．

［2］ 孙洪军，赵丽红．分形理论的产生及其应用 ［J］．辽宁工学院学报，2005，25(2):113－117．

［3］ Yu B M．Cheng P．A fractal permeability model for bi-dispersed porous media．Int J Heat and Mass Transfer ［J］．2002，(45):19－21．

［4］ 稻叶英男，武谷健吾，野津兹．流动过冷却水によろ连■制冰に阌する研究［C］．日本机械学会论文集，1992，58(548):1321．

［5］ 稻叶英男，武谷健吾，野津兹．静止状态におけるルク状水および水溶液の过冷却现象に影响を及ぼす诸因子の效果 ［C］．日本机械学会论文集，1993，59(560):1202．

［6］ 稻叶英男，武谷健吾．静止水の过冷却现象ぼす诸因子の影响［C］．日本机械学会论文集，1993，59(567):3557．