不确定响应时间下准时交货激励契约的协同研究

方忠民，陈治亚，曾明华

（1.中南大学交通运输工程学院，湖南长沙410075；2.华东交通大学轨道交通学院，江西南昌330013）

JIT采购（准时采购）是一种高水平的供应链采购运作管理模式，是从准时生产发展而来的，是为了消除库存和不必要的浪费而进行持续性改进，是准时化生产管理模式的必然要求。理想的准时采购是直到用户需求真正发生时才进行的少量多次的供应配送，且要求供应商企业具有高水平的供货质量，以获得满意订单采购交货效果。有研究表明，供应链中供应商企业和核心生产企业的采购行为动机对实施JIT采购具有一定影响，Hill[1]研究认为发展基于长期的、双赢合作关系模式的准时配送关系应建立供需（买卖）双方的充分信用和相互合作的承诺机制；由于JIT采购交货的准时性主要由供应商掌控，Iyer等[2]认为要保证供应商企业准时交货承诺的可靠性和稳定性，采购企业必须与供应商企业建立战略伙伴关系，并通过建立各种激励契约机制使供应商企业和采购企业一起分享准时化采购的好处。近来，不少研究者提出利用博弈模型进行研究[3-6]。

核心生产企业根据订单编制详细的采购计划，提前的采购交货会增加其库存成本，延期的采购交货会产生缺货成本；供应商企业根据核心生产企业的订单驱动的采购订单计划组织其产品生产和供应，由于生产运作与运输能力的相对固定，完成采购订单计划并交货的时间安排直接影响供应商企业的成本和收益，交货时间过长会增加库存成本，过短会增加赶工成本。在供应链系统中，成功实施准时采购需要依托供应链体系中上下游企业间的有效协调与合作[7-8]。

为了提高供应的准时交货概率和交货质量，降低供应链中的需求不确定性给核心生产企业所带来的影响，在供应链战略合作的体系框架下，双方应在供应商－供应商协同（内部协同）与核心生产企业－供应商博弈（外部博弈）的进程中，通过各自决策变量的设计，寻求有效的激励机制和最优的期望收益。

1 核心生产企业与供应商之间的Stackelberg博弈模型建立

1.1 基本假设

在建立模型之前，首先给出以下假设:

假定1 核心生产企业与供应商在协商并设计准时采购契约过程中的决策是基于完全信息的。

假定2 不考虑提前完工所带来的原材料、半成品和生产过程中所产生的库存持有成本。

1.2 符号说明

在模型构建与分析之前，首先给出一些必要的符号定义和参数说明如下。

Q为核心生产企业的采购总量,0＜Q＜Qmax；R为核心生产企业的采购价格；T为核心生产企业与供应商企业商定的采购订单计划完成时间，不允许提前完成订单交货，Tmin≤T≤Tmax；ti为供应商企业为完成订单计划所需的全部时间，假定其服从参数为λ的指数分布，且ti相互独立；f(t1,…,tN-1)与F(t1,…,tN-1)分别为供应商企业完成订单所需全部时间的联合概率密度函数与联合概率分布函数；B为核心生产企业为供应商企业准时完成订单计划交货提供的单位批量产品的激励奖金，0≤B≤Bmax；α为供应商企业的单位批量产品单位时间的库存成本，α＞0；β为供应商企业为保证及时交货的单位批量产品单位时间赶工成本，β＞0；δ为核心生产企业由于供应商企业未能及时交货而造成损失而引起的的单位批量产品单位时间缺货成本，δ＞0；Ep(B,Q)为核心生产企业成本的期望值；Es(T)为供应商成本的期望值。

1.3 Stackelberg博弈模型

在整个过程中，核心生产企业与供应商在准时采购-交付过程中的关系可视为一个完全信息的Stack⁃elberg主从博弈，双方追求在JIT采购中各自的期望成本最小化。

供应商的成本Es主要包括:提前完成订单的成本、延迟完成订单的成本，其中，提前完成订单的成本包括完工时间到交货时间的库存成本（因为不考虑提前交货），延迟完成订单的成本指延期所造成的赶工成本，它们分别与库存时间和延迟时间的大小成正比。

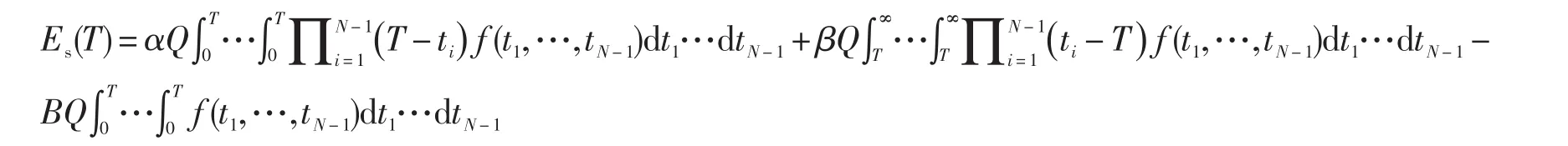
式中:第1项为预期库存成本，第2项为预期赶工成本，第3项是由预期可能得到的激励奖金。供应商企业的成本最小化问题就是我们所要考虑的最优化问题，即

核心生产企业的成本Ep主要由3部分构成:采购成本、为激励供应商而支付的成本以及供应商企业未能及时交货而造成损失而引起的短缺成本，其中，采购成本主要由采购批量和采购价格所决定，缺货成本随延迟时间的增加而增加。核心生产企业若主要考虑的决策变量为激励奖金B和采购量Q，其成本表达式如下

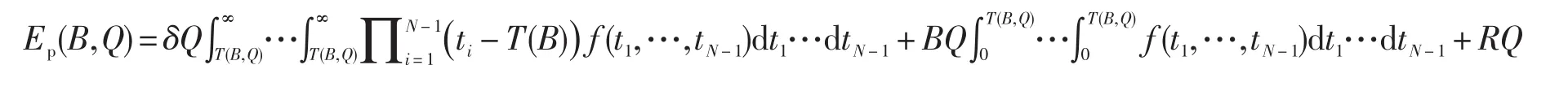
式中:第1项为预期缺货成本，第2项为预期奖金支付金额，第3项为为采购物品的价格支付。

核心生产企业依据成本最小化，即求解成本最小化的优化问题为minEp(B，Q)，s.t.0≤B≤Bmax，0＜Q＜Qmax，从而确定激励变量和采购量的值。

2 模型的最优性分析与最优决策

上述Stackelberg博弈模型的构建是为供应链中的节点企业提供决策支持，为此，需要分析该模型所涉及的各成员企业的决策是否存在最优均衡解。首先，不考虑约束情形，通过分析无约束情况下该主从博弈双方决策的最优性，可以得到如下的定理。

定理1 供应商的期望成本Es(T)的最优解满足如下最优性条件

考虑到本文研究供应商协同供货，将所有供应商作为一个整体，即只考虑一个供应商，得到上述一阶最优性条件的特殊情况，即取N=2，由上述表达式，此时一阶最优性条件如下

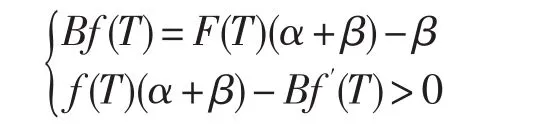
定理2 核心生产企业的期望成本Ep(B,Q)存在局部最优解。

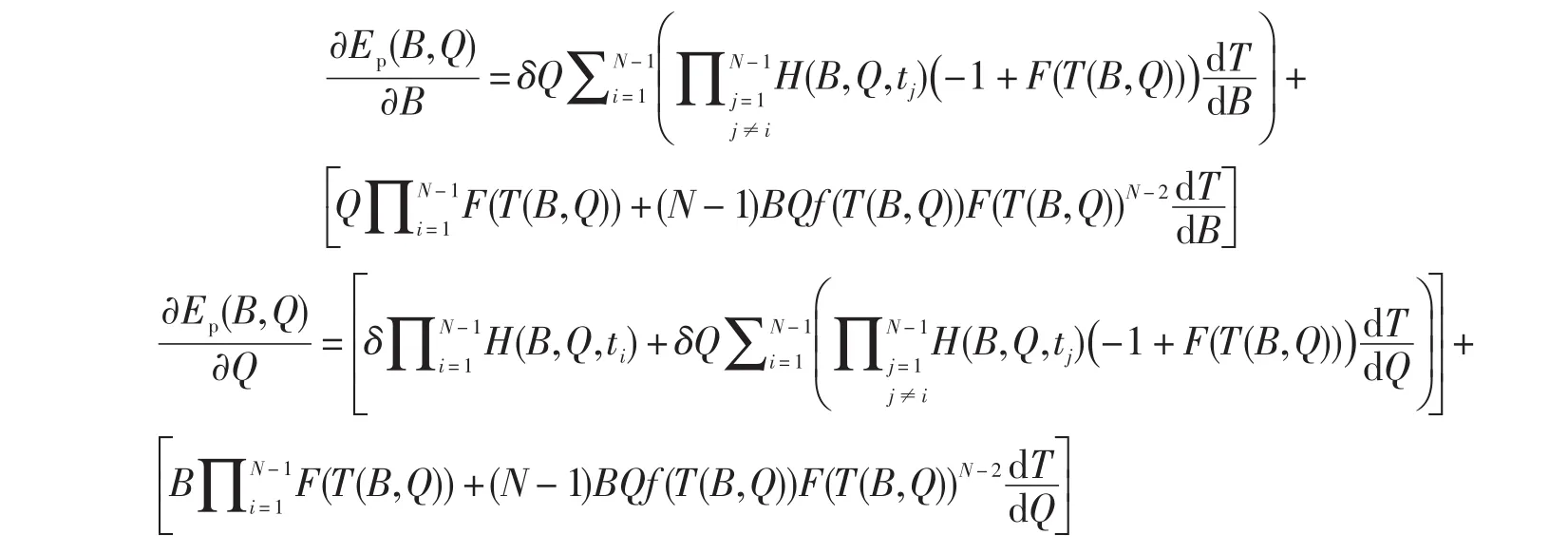
经过求解方程∇Ep(B,Q)=0，可以得到解点(B*,Q*)。

考虑到我们研究供应商协同供货，只考虑一个供应商，则得到上述定理的的特殊情况。取N=2，可以得到如下结论。

如果满足下列不等式条件

那么，核心生产企业的期望成本函数将存在局部极小值，且在(B*,Q*)处取得。

不难发现，尽管问题是相对复杂的，但只要知道供应商企业完成订单响应时间服从指数分布，通过上述理论分析，可以获得Stackelberg均衡解的必要条件，找到供应商成本函数的最优解和核心生产企业成本函数的局部最优解。如果核心生产企业成本函数具有凸性，那么，最优解同样可以通过理论分析取得。

3 内嵌内点法的模拟退火求解算法

考虑到双层规划问题的NP难性，利用模拟退火算法求解上层规划模型，结合内点法求解下层规划模型，从而构造核心生产企业与供应商企业之间的博弈模型的优化算法。

步骤1 给定初始可行解x0≜(B0,Q0)∈Ωp，其中Ωp={(B,Q)|0≤B≤Bmax,0＜Q＜Qmax}，设定初始温度，给出常数σ≥2，γ＞0，计算，置，置k←0；取初始惩罚因子R0=1＞0，容许误差ε＞0。

步骤3 利用当前迭代点Xk和随机向量Zk，产生一个新的试探点Ik=Xk+Zk，并计算Ep(Ik)。

步骤4 若Ik∈Ωp，则转步骤5；否则重新计算试探点

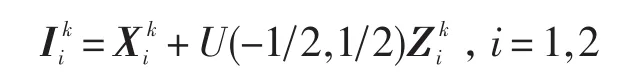
此时再次判断，若Ik∈Ωp，则转步骤5；否则继续上式计算，直到Ik∈Ωp并转步骤5。如果在设定的迭代步内始终有Ik∉Ωp，则令Ik=Xk，并转步骤5。

步骤5 产生一个随机数η∈U(0,1)，η≠0,1，计算在给定当前迭代点Xk和退火温度下接受试探点

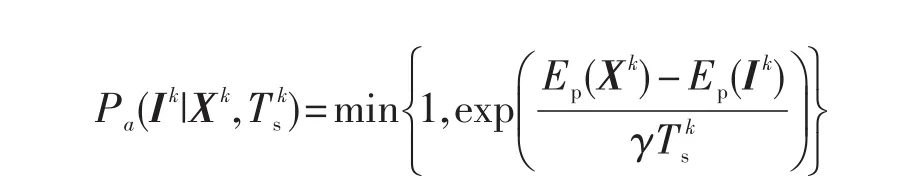
Ik的概率若Pa(Ik|Xk,Tsk)≥η，则置Xk+1=Ik，Ep(xk+1)=Ep(Ik)；否则置Xk+1=Xk，Ep(xk+1)=Ep(xk)。步骤6 若Ep(xk+1)＜Empin，则置xmin=xk+1，Empin=Ep(xk+1)。

步骤7 若满足迭代终止条件，则xmin即为近似最优解，Eminp为相应的最优值，同时，转入步骤8；否则，转步骤12。

步骤8 令y0=T0∈Ωs，其中，

步骤9 从yl-1点出发，用无约束最优化方法求解miny∈ΩsP(y,Rl)的极值点y*(Rl)，其中

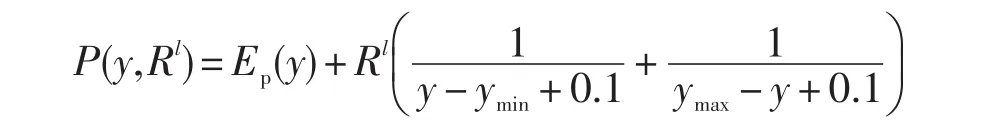
步骤10 检验终止迭代准则

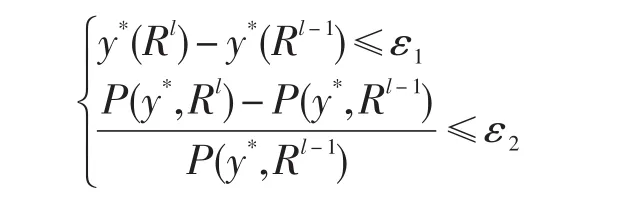
若满足，则停止迭代，并以y*(Rl)作为原目标函数Ep(y)的约束最优解，否则转步骤11。

步骤11 取Rl+1=ςRl，y0=y*(Rl)，置l←l+1，并转步骤9，其中，递减系数ς∈[0 .1,0.5]，这里取ς=0.1。

通过上述算法，可以求解得到核心生产企业与供应商企业根据各自成本函数所寻求的近似最优解。从模型与算法的构建的整个过程，都体现了供应商企业的协同，也很好地反应了处于主导地位的核心生产企业与作为跟随者的供应商之间的博弈行为。

4 结论

基于供应链战略合作伙伴关系的体系框架，从采购双方行为动机的角度出发，研究了不确定响应时间下准时交货激励契约的博弈与协同模型，并基于最优性分析设计了数值计算的优化算法，该算法通过模拟退火准则内嵌内点法搜索以实现近似最优求解。本模型和算法研究可提高供应的准时交货概率和交货质量的保证，最大程度降低供应链需求不确定性给核心生产企业所带来的负面影响，这对供应链协同管理具有重要参考价值。

[1]HILL C，JONES G R.Strategic management theory:an integrated approach[M].4th ed.New York:Houghton Mifflin，1998:98-101.

[2] IYER A V，BERGEN M E.Quick response in manufacturer-retailer channels[J].Management Science，1997，43（4）:559-570.

[3] GROUT J R，CHRISTY D P.An inventory model of incentives for on-time delivery in just-in-time purchasing contracts[J].Naval Research Logistics，1993，40:863-877.

[4]CHOI T M，LI D，YAN H，et al.Channel coordination in supply chains with agents having mean-variance objectives[J].Omega，2008，36（4）:565-576.

[5] KATOK E，WU D.Contracting in supply chains:a laboratory investigation[J].Management Science，2009，55（12）:1953-1968.

[6]骆世广，叶赛，胡蓉.基于多输出支持向量机的物流量预测研究[J].华东交通大学学报，2010，27（5）:68-69.

[7]杨文胜，马士华，李莉.供应链中准时采购的Stackelberg模型及决策[J].系统工程理论方法应用，2005，14（1）:68-73.

[8]李卓群.信息共享对树形供应链中的实体影响研究[J].华东交通大学学报，2010，27（3）:73-74.