矩阵值函数空间中尺度空间的稠密性
崔丽鸿,陈晓东,杜俊峰,王隆玉,郭兴宝,崔月娥
(北京化工大学理学院数学系,北京 100029)
矩阵值函数空间中尺度空间的稠密性
崔丽鸿,陈晓东,杜俊峰,王隆玉,郭兴宝,崔月娥
(北京化工大学理学院数学系,北京 100029)
多分辨分析的概念在小波基构造中起着非常重要的作用,并经历了从经典多分辨分析到多重多分辨分析,再到矩阵值多分辨分析的研究历程.本文基于矩阵值多分辨分析,研究并给出了矩阵值函数空间中尺度空间稠密性的两个充要条件,并在此基础之上得到了稠密性的两个充分条件.
矩阵值多分辨分析;矩阵值函数空间;尺度空间;稠密性
1 研究背景
1981 年,文献[1]提出了小波的正式概念之后,经过30年的发展,小波分析理论及应用的相关研究取得了重大的进步,并成为国际上公认的新方向和热点,是数据处理、特征识别等方面所使用的非常前沿且有效的工具.1987年,文献[2-4]提出了多分辨分析的概念,统一了此前所有具体正交小波的构造.1998年,文献[5]首次引入了矩阵值多分辨分析和对应的矩阵值小波基的概念,基于此,文献[6-7]研究了矩阵值小波的构造问题,文献[8]给出了向量值双正交小波的存在及构造问题,尽管得到了较好的研究结果,但尺度函数通过平移变换和伸缩变换所张成的尺度空间在全空间中的稠密性又是多分辨分析理论中一个非常重要的条件,因此尺度空间稠密性的研究,对于小波函数构造理论至关重要.本文主要研究在矩阵值小波分析理论中,尺度函数空间在整个矩阵值函数空间的稠密性问题.
2 矩阵值L2-函数空间
本节先给出全文用到的相关定义.
定义2.1设t∈ℝ,fkl(t)∈L2(ℝ),k,l=1,2,…,N,则定义矩阵值L2-函数空间为:
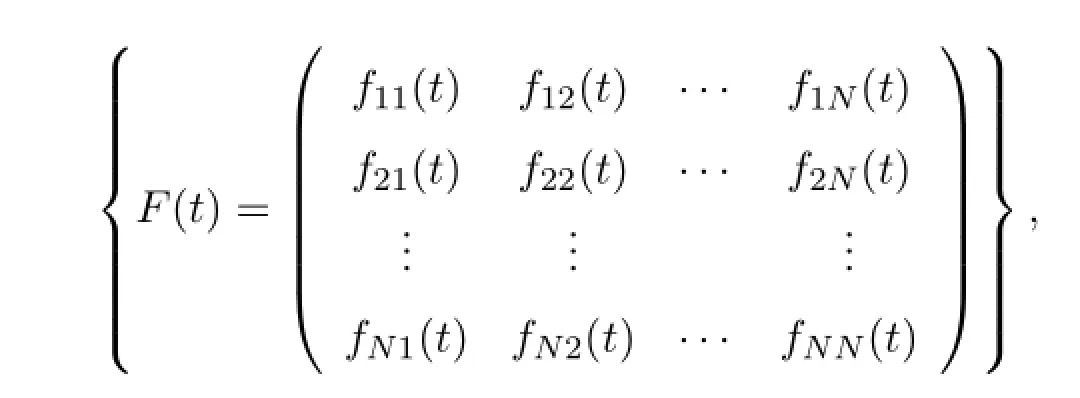
记作L2(ℝ,ℂN×N),该空间中的函数F(t)称为矩阵值函数.
在此基础上,可以引入相应的范数、内积等一系列定义:

定义2.2设F(t)=(fij(t))N×N∈L2(ℝ,ℂN×N),则矩阵值函数F(t)的平移F(t-k)定义为F(t-k)=(fij(t-k))N×N,其中k∈ℝ,记作Fk(t).
定义2.3 F(t)=(fij(t))N×N∈L2(ℝ,ℂN×N),则矩阵值函数F(t-k)的伸缩F(m t)定义为F(m t)=(fij(m t))N×N,其中m∈ℝ.
在明确了这些定义的基础上,来研究尺度函数空间在整个矩阵值函数空间的稠密性问题.
3 尺度空间的稠密性


由于每个Φn都是在X中,因此有supp cφn⊂Ω几乎处处成立,因此有Ω0⊂Ω几乎处处成立.
设Ω1=ΩΩ0,假设Ω1的测度大于0.由命题3.2可知,∀s∈Vn,都有supp b s⊂supp cΦn.由于对于任意n∈ℤ,cΦn在Ω1上都是不存在的(即在Ω1上为0),对Vn中每个矩阵值函数做傅里叶变换,则有∪Vn中的每个矩阵值函数在Ω1上都是不存在.
因此,如果可以证明如果在X中每个矩阵值函数的傅里叶变换在Ω1上都是不存在,那么Ω1模为0,Ω与Ω0相差一个模为零的集合.否则与b X=L2(Ω,ℂN×N)矛盾.
任取F∈X,∃G∈∪Vn,满足b G在Ω1上不存在.则


证明因为Φ是紧支撑的,因此bΦ=0成立的点的集合,即Z(bΦ)为零测集,由定理3.2可直接得到此推论.
至此,由定理3.1和定理3.2得到了矩阵值函数空间中尺度空间稠密性的两个充要条件,由推论3.1和推论3.2给出了两个充分条件.
4 结论
本文基于矩阵值多分辨分析理论中尺度空间的定义,通过一系列证明,最终给出了矩阵值函数空间中尺度空间稠密性的两个充要条件,相信这对矩阵值小波函数的构造提供了很好的理论依据.并在此基础之上给出了两个加强了的充分条件,这将使得矩阵值小波的构造更加方便.
致谢感谢北京化工大学2011年大学生科技创新基金重点项目以及2011年国家大学生创新性实验计划立项项目(101001027)对于本文的支持.感谢审稿人的有益建议.
[1] Morlet J. Wave propagation and sampling theory and complex waves[J]. Geophysics, 1982,47(2):222-236.
[2] Mallat S. Multiresolution approximations and wavelet orthonormal bases of L2(R)[J]. Trans. Amer. Math.Soc., 1989,315(1):69-87.
[3] Daubechies I. Ten Lectures on Wavelets[M]. Philadelphia: SIAM, 1992.
[4] Ron A, Shen Z. A±ne systems in L2(Rd): The analysis of the analysis operator[J]. Journal of Functional Analysis, 1997,148(1):408-447.
[5] Xia X, Suter B. Orthonormal matrix vector-valued wavelets and matrix karhunen-loeve expansion[J]. Con- temporary Mathematics, 1998,216(1):159-175.
[6] Cui L, Zhai B. Existence and design of biorthogonal matrix-valued wavelets[J]. Nonlinear Analysis Series B:Real World Applications, 2009,10(5):2679-2687.
[7] Cui L, Zhang T. M-Band orthogonal vector-valued multiwavelets for vector-valued signals[J]. Journal of Applied Mathematics and Computing, 2008,28(1/2):165-184.
[8]陈清江,陈瑛.向量值双正交矩阵值小波的存在性及滤波器的构造[J].纯粹数学与应用数学,2008,24(1):10-16.
[9] Boor C, Devore R, Ron A. Approximation from shift-invariant space of L2(Rd)[J]. Transactions of the American Mathematical Society, 1994,341(2):787-806.
[10] Dong B, Shen Z. MRA-based Wavelet Frames and Applications[M]. Salt Lake City: Park City Mathematics Institute, 2010.
The density of the space of matrix-valued scaling function
Cui Lihong,Chen Xiaodong,Du Junfeng,Wang Longyu, Guo Xingbao,Cui Yuee
(Faculty of Mathematics and Computer Science, Beijing University of Chemical Technology,Beijing 100029, China)
The multiresolution analysis is a very important to construct the wavelet basis. From the classic multiresolution analysis to the multiwavelets multiresolution analysis and the matrix-valued multiresolution analysis, the content of the MRA has been greatly development. In this paper, we discuss the density of the space of matrix-valued scaling function which is based on the space of matrix-valued functions. And finally, we give two necessary and su±cient conditions and two su±cient conditions of the density.
matrix-valued multiresolution analysis, the space of matrix-valued functions, the space of matrix-valued scaling function, density
O174.2
A
1008-5513(2012)02-0143-06
2011-10-10.
大学生创新性实验计划(101001027).
崔丽鸿(1965-),博士,教授,研究方向:小波分析理论、算法及在图像处理中的应用.
2010 MSC:42C40,65T 60

