遗传神经网络在车身姿态测量中的应用

吴学文 吴黎明 张力锴 陈泰伟

（广东工业大学信息工程学院）

1 引言

汽车的安全、舒适、便捷系统已经成为许多消费者买车的主要考虑配置之一[1]。随着汽车工业与电子工业的不断发展，电子技术在现代汽车上包括汽车电子系统方面的应用越来越广泛[2]。大部分汽车电子系统都需根据车身的状态信息即车身姿态的反馈，做出相应的动作来确保汽车的安全和舒适。

早期采用机械转子陀螺构成机械平台来测量汽车姿态，由于体积大、安装不便等缺点，使其在汽车上的应用受到很大限制。目前，一般利用三维陀螺仪测量车身姿态，并通过加速度计等惯性传感器不断作数值修正。由于陀螺仪本身随着时间、外界温度变化，会产生不同程度的漂移[3]，且采用六个或九个单轴线加速度传感器[4～6]，再利用欧拉法、方向余弦法或四元数法解算出姿态角[7]，存在系统复杂、成本高和实时计算难等缺点，因此应用于工程实践受到限制。

针对上述问题，本文提出了一种精简的汽车姿态测量方法，即在满足精度的前提下，利用单个三轴加速度传感器和高性能MCU构建车身姿态测量系统。将三轴加速度映射到车身姿态角，但该映射输入、输出以及结构参数之间的复杂动态关系，难以建立精确模型。随着神经网络的出现，为解决系统建模带来新的思想。近几年神经网络被用于建模中并取得一定的成果，但神经网络全局搜索能力差、收敛速度慢，容易陷入局部极值，单独使用效果不够理想。为此本文提出用具有全局搜索能力的遗传算法和神经网络相结合，实现三轴加速度映射到车身姿态角。

2 加速度与姿态角的映射关系

2.1 坐标系与姿态角

为便于分析，建立两个坐标系，分别是汽车导航坐标系OXYZ和汽车平台坐标系Oxyz，如图1所示。

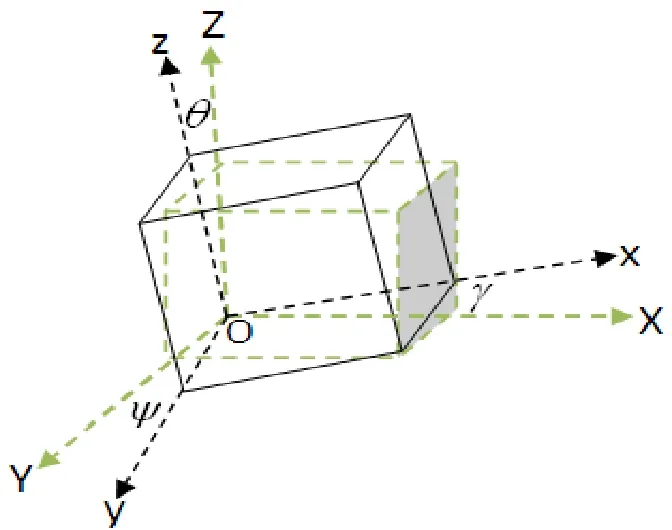
图1 坐标系与姿态角

2.2 平衡状态下姿态角的测量

车身姿态测量就是要测量出两坐标系相对角度偏移量，根据导航学转动变换中的欧拉定理，汽车的姿态可用相对汽车平台坐标系相应轴的一次转动来表示。将OXYZ坐标系绕X轴旋转θ角，再将所得的坐标系绕Y轴旋转γ角，最后将坐标系绕Z轴旋转ψ角得到坐标系为Oxyz。每次转动的角度分别为：俯仰角θ、倾斜角γ、偏航角ψ。

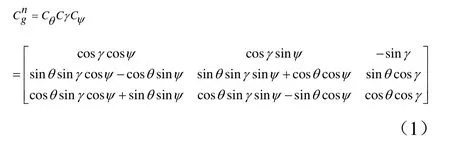
以往车身姿态角测量方案需在车身安装多个传感器，本文设计一个精简的车身姿态测量方案，只需在车身质心处安装一个三轴加速度传感器，并以此为汽车平台坐标系。

三轴加速度传感器传统意义上反映的是当前运动物体的线加速运动状态。基于MEMS原理的加速度传感器是利用惯性体的惯性形变从而测量加速度，反映的是合外力对载体运动加速度的影响。在平衡状态下（包括汽车静止或匀速运动），加速度传感器反映的是地球的万有引力加速度。当汽车平台坐标系Oxyz与汽车导航坐标系OXYZ重合时，输出的值用向量表示为当两坐标系间有角度偏移时，输出且加速度计测量值是重力加速度在汽车平台坐标系三轴的分量。重力加速度的方向始终向下，大小为g（g为当地的重力加速度）。因此有：

根据式（1）和式（2）可得车身在平衡时的姿态角γ、θ：

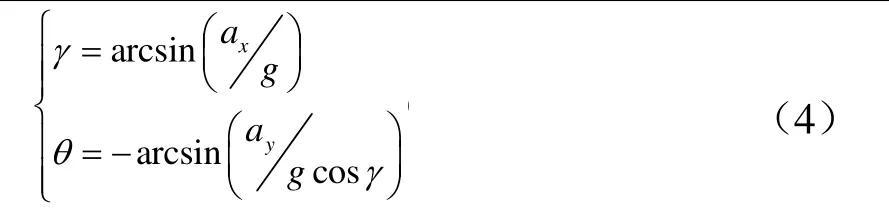
由式（4）可知，在汽车平衡状态下，加速度与汽车姿态角是一一映射关系。

2.3 加速运动状态下姿态角的测量

汽车加速运动状态可分解为：① 前向加速度或减速度（x轴）；② 转向时离心力作用下的离心加速度（y轴）；③ 路面不平汽车上下摇摆的向心加速度（z轴）。多数情况下汽车运动是三个轴的加速度同时结合，下面将对其进行立体分析。由于汽车运动的特殊性，可以对其三维加速度作非线性分类，识别出汽车当前处于何种运动状态，计算出加速度传感器输出的有害惯性分量，并可据此修正得到原始角度向量，从而映射出正确的姿态角。针对汽车运动模式可分类的特点，合外力的作用方向可以巧妙地估计出并被唯一的确定。

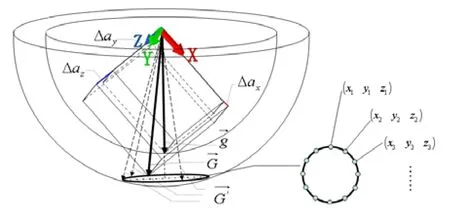
图2 运动姿态参考基准分析

如何保证上述唯一性：① 汽车运动通常的姿态角度不大，除非是越野车翻越障碍时比较明显，一般的轿车行走时俯仰角<30°、倾斜角<15°，据此可以有效地控制输出结果的范围；② 汽车运动有其惯常模式，例如左转弯时必然导致车身向右侧倾斜，向前加速时必然导致尾沉。因此，三轴加速度与实际的姿态角度必然有其内在对应关系，而这种排他的对应关系，为映射提供了一种选择的规则参考；③ 在具体的神经网络结构中，引入了状态变量，即网络输入量不仅仅是三轴加速度的当前量，还包括其变化量，由此可以推导出当前的三轴加速度是由何种状态过渡而来的，结合汽车运动惯常模式，利用简单的推理机制解决了前文所述的带有不确定性的严重非线性映射问题。

3 遗传神经网络

从上述可知，汽车无论是在平衡状态下还是运动状态下，汽车姿态角都能由三轴加速度唯一地确定，但是三轴加速度映射到姿态角是一个复杂的非线性特征和时变性的函数关系，难以建立精确的数学模型。传统的方法需要先建立系统数学模型，再进行算法设计，最后在各种处理器上实现算法。在工程实际应用中依赖数学模型的控制方法日益受到制约，传统方法应用于此不适合。本文利用神经网络逼近任意非线性函数的能力，来模拟实际系统的输入输出关系；同时利用神经网络的自学习自适应能力，可以方便地给出工程上易于实现的学习算法，经过网络训练最终得到系统的正向或逆向模型[8]。

目前应用最广泛的神经网络是BP神经网络，大部分神经网络模型是采用BP算法或它的演变形式，但它存在容易陷入局部极小值和对初始权值具有较强的依赖性问题。国内外许多学者对其进行了研究，提出了许多方法克服BP算法的缺陷。将遗传算法与BP算法融合是有效方法之一，它充分利用了遗传算法的全局搜索能力和BP算法的局部搜索能力，克服了BP算法容易陷入局部值、收敛速度慢的缺点[9]。

遗传算法对神经网络的优化包括对神经网络结构和网络权重的优化。网络权重优化基本原理是利用遗传算法选择出最优个体，从个体得到优化后权重，通过选择、交叉和变异操作找到最优适应度值对应的个体。遗传神经网络中如何定义适度函数非常关键，适度函数直接关系到最优个体即优化后权重。若输出输入样本总数为n；输出层节点为m；第p个样本的第l个节点的期望输出值为tpl；第p个样本的第l个节点实际输出值为opl，一般可用神经网络误差平方和的倒数作为适应度函数：

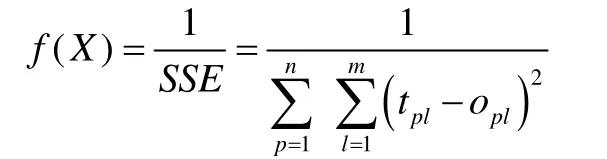
遗传神经网络先利用遗传算法，全局搜索网络权值，作为神经网络的初始权值，再通过神经网络训练进一步修改权值，以达到精确求解。该网络（GA-BP）算法分为三步：

(1)固定网络结构和编码生成初始种群。采用6-8-2型网络结构，具体的结构如图3 所示。输入量为三轴加速度当前量和三者的增加量，结合当前的增加量可以得知其由何种状态转换而来，从而建立更加准确的映射关系。系统还引入陀螺仪实时输出两轴向的角加速度，将其输出数值积分后得到实际姿态角作为神经网络训练样本。采用实数编码对权值和阀值进行编码，它比二进制编码更精确、更稳定。

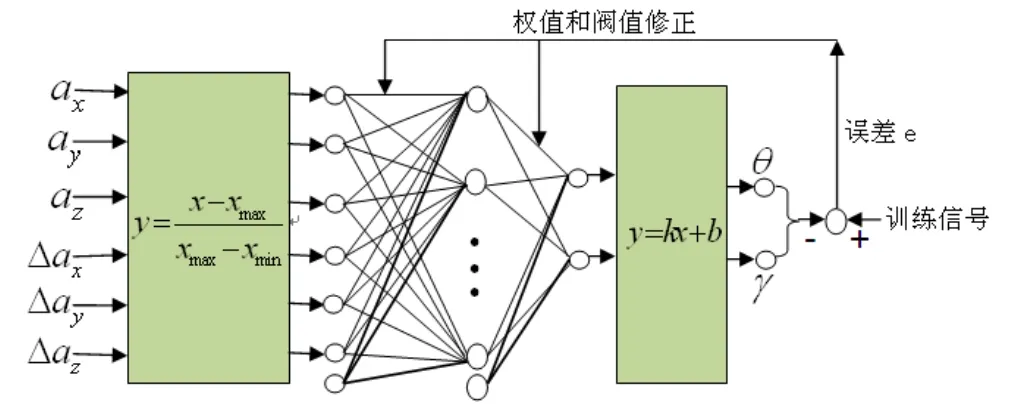
图3 神经网络结构图

(2)遗传算法进化。对个体进行选择、交叉和变异操作，并结合适应度函数求出最优个体。个体选择算子采用轮盘赌法，交叉算子：若个体 x1、 x2交叉运算后得到两个新个体其中为两个新个体；a为交叉概率，在此a取值为 0.4。变异算子为：其中分别为变异前后的权值或阀值；λ为0到1的随机数； Emax(t)为最大适应度的个体误差。

(3)神经网络训练。从最优个体中提取权值和阀值作为网络初始权值和阀值，再通过网络训练更改权阀值直至满足系统误差要求。GA-BP算法流程图如图4所示。

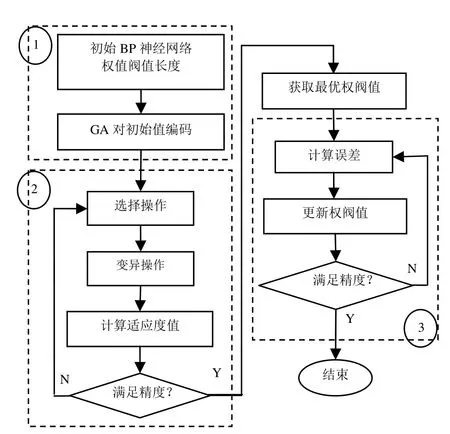
图4 GA-BP算法流程图

4 实验结果分析

利用廉价的 FPGA、ADXL203型加速度计和ADXRS150型陀螺仪搭建硬件平台，用大约6小时采集的6000组数据作为神经网络训练样本，样本由输入信号（加速度）和训练信号（姿态角）组成。加速度用单个加速度计采集，姿态角由陀螺仪采集角加速度，然后再通过积分得到数据。网络需要利用样本不断地训练直至陀螺仪反映的姿态角与经过网络映射所得的姿态角的误差满足精度要求时，才固定网络的连接权值和阀值，最后把陀螺仪从系统拆除，实现网络本身映射姿态角。

经过训练后，神经网络（GA-BP）映射的俯仰角θ、倾斜角γ与陀螺仪（Gro）的输出θd、γd相比如图5所示。

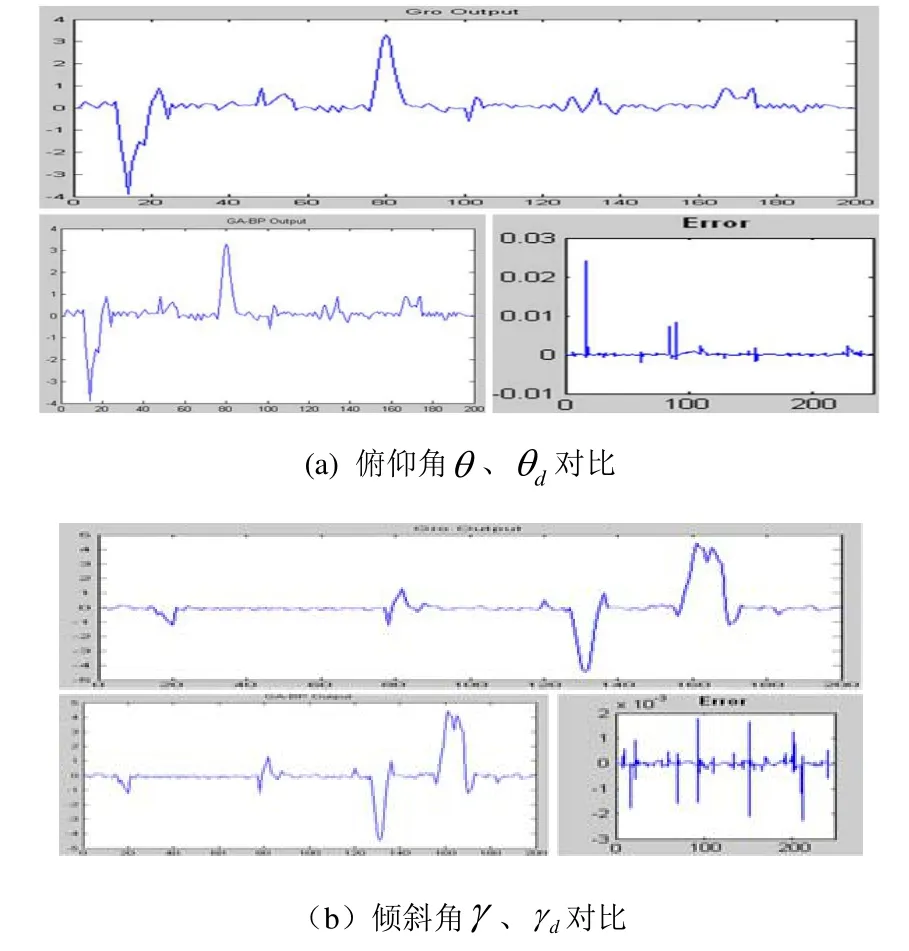
图5 神经网络与陀螺仪输出比较

图（a）中曲线扰动幅度最大的两处，分别是由于汽车行驶时加速（尾沉）和减速（点头）引起前后倾斜。图（b）中也有两处大幅度扰动，分别是由汽车左右拐弯引起的右侧倾斜和左侧倾斜。经过训练后的GA-BP神经网络能精确映射出车身姿态角，其误差小于0.03，满足汽车运动姿态测量的精度要求，说明了该测量方案可行。神经网络的并行结构使用传统的软件实现速度慢，可以利用FPGA的可配置性和并行性加速其实现。

5 结论

本文设计一种精简的汽车运动姿态测量方案，该方案只使用单个加速度计测量出汽车运动姿态，具有成本低、不需复杂的数学建模、适应性强等优点。本文通过将遗传算法与 BP网络结合起来，克服了 BP网络的局部收敛缺陷，提高了神经网络的学习速度和预测精度。并利用神经网络的非线性映射能力、泛化能力和容错能力解决上述方案非确定性的多输入多输出映射问题。详细地分析了加速度映射姿态角，利用MATLAB进行仿真实验，结果显示，该方案满足精度要求，确实可行。

[1]史临潼,黄日昌,赖鹃,等.现代汽车安全舒适便捷系统综述[J].汽车电器,2007,10.

[2]许林.现代汽车电子技术的发展前景[J].科技论坛,2007,4.

[3]秦勇,臧希喆,王晓宇,等.基于 MEMS惯性传感器的机器人姿态检测系统的研究[J].传感技术学报,2007,20(2).

[4]高宗余,李德胜.多MEMS传感器姿态测量系统的研究[J].电光与控制,2010,17(3).

[5]Xue Liang,Yuan Weizheng,Chang Honglong,et al.MEMS-based Multi-sensor Integrated Attitude Estimation Technology For MAV Applications[C]. Conference on Nano/Micro Engineered and Molecular Systems.China.2009,1.

[6]李怡凡,吴黎明,张力锴.一种车身姿态的捷联测量[J].传感技术学报,2010,23(8).

[7]贾宏光,陈涛,张跃.基于四元数法的捷联式惯性导航系统的姿态解算[J].光电精密工程,2008,10.

[8]王俊国.基于神经网络的建模方法与控制策略研究[D].华中科技大学,2004,5.

[9]黄庆斌.BP算法的改进及其应用研究[D].西南交通大学,2010,5.