单周-PID控制buck电路在DCM模式下的研究

李鹏 吴浩伟 周樑 徐正喜

（武汉第二船舶设计研究所，武汉 430064）

0 引言

单周控制是由美国学者Smedley和Cuk教授在上个世纪90年代提出的一种新型的大信号、非线性的控制策略[1]，即在一个开关周期内，强制积分变量的平均值与参考值相等，以此来实现对时变电压或电流的瞬时控制。

单周控制的开关变换器[2]，可分为连续导电（CCM）和不连续导电（DCM）两种工作方式。在一个开关的周期内，其能有效地抑制输入扰动，结构简单、响应速度快。但是抑制负载扰动能力均较差，特别是在轻载的情况下，有时会发生超调或者阻尼震荡的现象。为了改善单周控制，必须将单周控制和PID控制结合起来。本文首先建立单周控制在DCM下的连续时间模型[2]，在单周控制的基础上设计PID控制器，将单周控制和PID控制相结合，组成单周-PID闭环控制系统[3]，并比较单周-PID控制与单周控制的输出特性。

1 连续时间模型的建立

以buck变换器为例，建立连续时间模型。

图1中，当buck电路工作在DCM模式下时，一个开关周期Ts分为三个阶段：T1，开关管S导通，二极管D截止，二极管的两端电压Ud=Uin；T2，开关管S断开，二极管D续流，Ud=0；T3，开关管S断开，二极管D截止，Ud=Uo。

参考电压Uref的表达式如下式1所示：

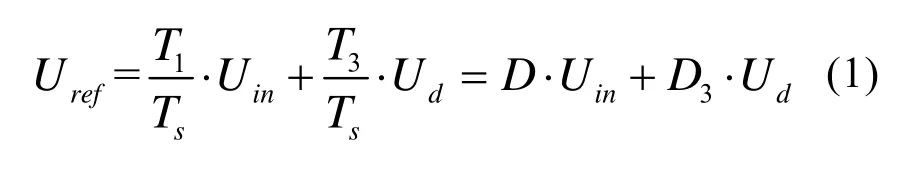
图1 单周控制的buck变换器

采用小信号模型进行分析，得到动态模型：

式（2）中大写符号为稳态值，小写带箭头符号为瞬时值。由于 T3时段内二极管 D两端的电压Ud等于输出电压Uo，因此用Uo取代Ud。

在实际的计算机控制系统中，第K个开关周期的占空比Dk取决于上一个周期，即K-1个周期二极管D两端电压Ud的取值。前面的式1并没有将前一个周期的状态考虑进去，为此，将式 1进行改进，得到参考值如式3所示：

由于开关频率fs远高于系统的带宽，在一个开关周期内，可以近似的认为输出电压Uo和输入电压Uin为常量。因此，式3可简化为：

对于式（4），考虑系统在扰动下的动态模型，得到单周控制器的离散表达式如下：

将上式（2）的动态模型转化为 Z域下的模型：

进一步，将式（6）中的z用指数项 esTs替代，

同时考虑采样保持器的因素：

得到单周控制的最终模型如下：

对于指数项 esTs和 e-sTs，用泰勒级数表示：

用泰勒级数的一阶展开式来近似，得到：

DCM模式下控制到输出的传递函数[4]如下：

由式（10）、（11），得到参考值到控制的传函：

由式（11）、（12），参考值到输出的传函如下：

根据上式（11）、（12）和（13），可以得到单周控制的连续时间模型[2]如下图2所示。

图2 单周控制的连续时间模型

从此图中可以看出，由于输出滤波器的模型独立于单周控制器之外，当负载发生变化时，输出滤波器的参数发生变化，这样负载扰动越过了单周控制器，影响到整个控制系统。此图说明，单周控制不能有效的抑制负载扰动，为了改善单周控制的缺点，得到单周控制的连续时间模型后，需在此基础上设计PID控制器，引入输出反馈，组成一个闭环控制系统。

2 PID控制器的设计

以 buck变换器为例，设计单周-PID控制系统。如下图3所示：

图3 单周-PID控制的buck变换器

此buck变换器可以看成双环控制系统，内环为单周控制，外环为 PID控制。负载电压 Uo与参考电压 Uref进行比较，得到误差信号，此误差信号经过PID控制器，生成参考值，与二极管D两端电压Ud的积分值进行比较。

图4 单周-PID控制系统的小信号模型

根据图2和图3，可以得到图4的单周-PID控制系统的小信号模型。采取经典的方法[5]设计PID控制器，为了使单周-PID控制系统能正确的运行，必须满足以下条件[3]：

式（14）中Mmax和Mmin为buck变换器的最大与最小变压比，uc即为图4小信号模型中的PID控制器的输出。

3 单周-PID控制系统的仿真

以buck电路为例，用MATLAB对整个控制系统进行仿真。Buck电路的参数如下：

输入电压Uin为15 V，参考电压Uref为5 V，滤波电感L为500 μH，电容C为20 μF，负载R为200 Ω，开关频率 fs为100 kHz。

图5为单周-PID控制buck变换器的主电路图，图6为控制电路图。

图5 单周-PID控制buck变换器主电路图

图6 单周-PID控制buck变换器控制电路图

当负载R为200 Ω时，此时的buck变换器工作在DCM模式，首先建立单周控制buck变换器的连续时间模型，在此基础上得到参考值到输出的传递函数Guref(s)，其伯德图如下：

图7 单周-PID控制传函Guref (s)伯德图

通过分析传递函数Guref(s)的伯德图，采用传统的方法设计PID控制器[5]，可以得到带输出反馈的单周-PID控制系统。下面来比较单周-PID控制系统与单周控制系统的输出特性。

图8 单周控制buck变换器输出电压

图9 单周-PID控制buck变换器输出电压

图10 单周控制buck变换器输出电压纹波

图11 单周-PID控制buck变换器输出电压纹波

图12 单周控制buck变换器负载扰动波形

图13 单周-PID控制buck变换器负载扰动波形

从图 8至图 13，通过比较单周控制与单周-PID控制buck变换器的输出电压波形，得到以下结果：单周-PID控制系统与单周控制系统相比，动态响应的速度更快，抑制负载扰动的能力更强，输出电压的纹波更小，不存在稳态误差。不论是动态性能，还是稳态性能，都有了很好的改善。

4 结论

本文主要研究单周控制的buck电路在DCM模式下的工作状态。通过建立单周控制buck电路的连续时间模型，在此基础上设计PID控制器，组成一个单周-PID的闭环控制系统。该系统综合了单周控制与PID控制的优点，与原有的单周控制系统相比，有更好的动态与稳态性能，并能有效的抑制负载扰动，具有较强的实用价值。

[1]K. M. Smedley, S. Cuk. One-cycle Control of Switching Converters[J]. Power Electronics, IEEE Transactions on November 1995,10(6)： 625-633.

[2]L. Egiziano, N. Femia. Dynamic Model of One-Cycle control for converters operating in CCM and DCM [C].IEEE Industrial Electronics, IECON 2006-32nd Annual Conference on 6-10 Nov 2006： 2150-2155.

[3]Mohsen Ruzbehani, Luowei Zhou. A New Approach in Combining One-Cycle Controller and PID Controller[C].Industrial Electronics,2004 IEEE International Symposium on May 2004,2：1173-1177.

[4]Dragan Maksimovic, Robert Erickson. Fundamentals of Power Electronics[M]. Second Edition, Kluwer Academic Publishers Group, January 2001.

[5]胡寿松. 自动控制原理[M]. 第四版, 北京： 科学出版社, 2001.