正态圆分布下的双机吊放声纳扩展方形搜潜建模

罗木生， 姜青山， 侯学隆

(海军航空工程学院，a.研究生管理大队;b.指挥系，山东烟台 264001)

0 引言

双机协同反潜，既可以实现快速地对可疑海区进行搜索，且发现目标后便于协同攻击，是直升机协同反潜的重要样式［1］。吊放声纳以其重量轻、携载方便，使用灵活，可根据海区环境选择最佳工作深度，有效作用距离较远等特点，已成为反潜直升机重要搜潜器材之一。

国内外对反潜直升机使用吊放声纳搜潜的研究较多［1-10］，也取得了许多重要成果。其中，文献［3-5］采用解析法建模计算了吊放声纳的搜潜概率;文献［6-7］对扩展方形进行了研究，并得出了一些结论。但是，运用解析法建立多机扩展方形搜潜概率模型的相关文献很少。

扩展方形一般运用于目标航向未知时的应召搜潜［11］，这种情况下，目标分布具有对称性。常被研究的多机扩展方形阵［6］不具有对称性，搜潜概率偏低。因此，本文以双机使用吊放声纳应召搜潜为例，采用解析法，在建立扩展方形搜索概率计算模型的基础上，提出了双机对称扩展方形搜索法，最后通过仿真计算，对比分析了两种搜索方法。

1 目标位置分布

要计算搜索概率，首先要分析目标的运动与位置变化。应召反潜时，获知的信息一般包括最后接触时的目标位置坐标、坐标精度，可能还有目标航速、航向等。设获知的信息为:目标位于半径Rc的某圆形区内的概率为p1，圆心坐标已知，航速、航向未知。

假定目标位置服从等方差相互独立的二元正态分布［3］，即正态圆分布，以圆心为原点、纬度方向为X轴(东为正)、经度方向为Y轴(北为正)建立坐标系，则t0=0时刻的目标位置分布密度函数为［12］

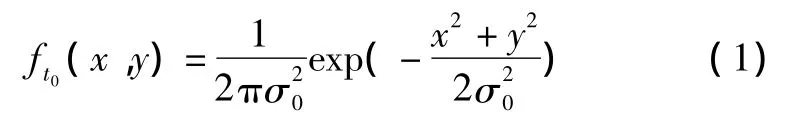
设目标航向、航速分布密度函数分别为fΨ(ψ)、fV(v)，则 t时刻目标位置密度函数［12］为

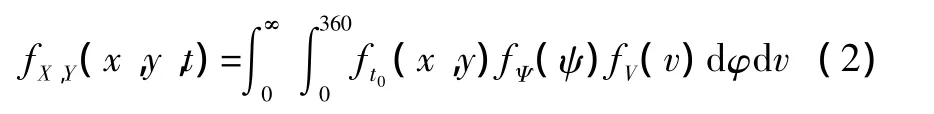
若目标航向服从［0，360］内均匀分布、航速服从参数v0的瑞利分布，则目标位置密度函数为［12］

2 吊放声纳搜索概率计算模型

吊放声纳搜潜为离散形式［11］，所以，搜索概率的计算分为两个步骤:首先计算单次探测的概率，然后计算整个搜潜行动的任务搜索概率。

2.1 单次探测概率

吊放声纳探测一次的区域为:以探测点为圆心，有效作用距离为半径的圆;故探测概率为目标位置分布函数在该区域内的积分。那么，吊放声纳探测时刻为t、到坐标原点距离为r'时的探测概率为［3］

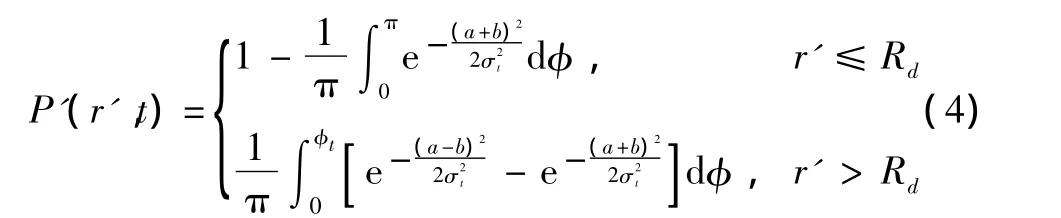
式(4)是独立探测一次的发现概率，没有考虑各次探测之间的影响。若假定已探测且没发现目标的区域不会有目标出现，忽略探测重叠区域，则ti时刻进行第i次探测的探测概率为

2.2 单次探测概率的修正

实际上，已探测区内不出现目标的面积会随着时间的推移而逐渐衰减，由于吊放声纳探测区为圆形，也就是每个已探测区圆的半径会衰减直至为0。衰减的程度由目标运动速度与衰减时间决定，则第i次探测时，第j(j≤i)次探测区的半径衰减为

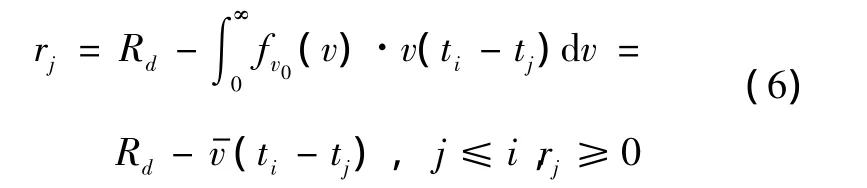
如果目标航速服从参数 v0的瑞利分布，则=。

文献［3］在假定已探测区的探测概率不随时间变化的前提下，引入概率衰减因子β，给出了第i次的探测概率计算公式

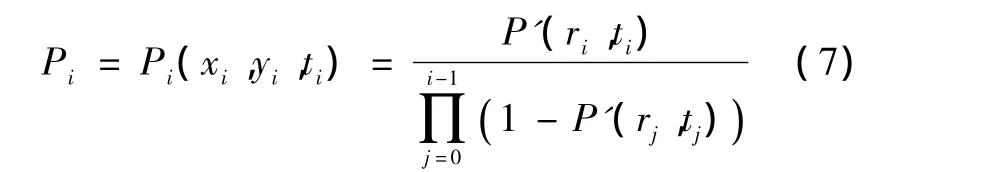
2.3 任务搜索概率

反潜直升机执行搜索任务时，设总共使用吊放声纳探测n次，则该任务下总的发现概率，即任务搜索概率为［3］

第n次探测时第一次发现目标的概率为［12］

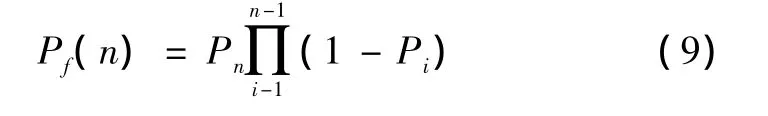
3 双机吊放声纳扩展方形搜索

使用吊放声纳搜潜时，执行不同的任务所采用的搜索方法也不同。当执行应召反潜时，吊放声纳搜索方法主要有扇形搜索、扩展方形搜索、螺旋线搜索等［1］。当目标航向未知时，一般从后两种方法中选择。直升机数量一般为单机或多机，为提高搜潜效能，常常采用多机协同搜索。本文重点分析双机扩展方形搜索，其他搜索样式的分析方法类似。

3.1 双机扩展方形搜索

双机扩展方形搜索方法如图1所示，相关研究文献较多［6-7］，各悬停点的坐标计算模型可参考文献［6］。为简化分析，同样忽略探测重叠区域，并假设双机开始第i次探测的时刻相同=ti，则双机第 i(i=1，2，…，n)次探测概率为

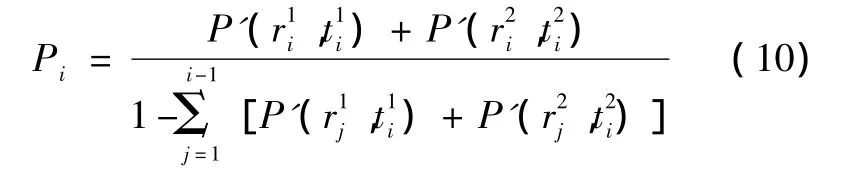
相邻两次探测时间间隔取决于直升机在两探测点之间机动的时间、一次收放吊放声纳与听测的时间。机动时间受风向、两点间距、直升机飞行速度等因素的影响，计算较为复杂，这里简化处理为间距与直升机平均飞行速度的比值。当确定吊放声纳工作深度后，收放与听测的时间一般为定值。所以，第i次探测的时刻为

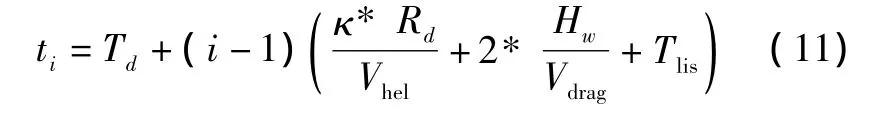
式中:Td为首次听测距t0的时间;κ为相邻探测点的间距系数，一般取1.2～1.8;Vhel为直升机平均飞行速度;Hw为吊放声纳工作深度;Vdrag为平均吊放速度;Tlis为单次听测时间。

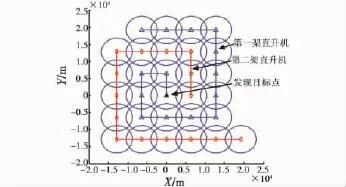
图1 双机扩展方形搜索示意图Fig.1 Two helicopters extended squared search

3.2 双机对称扩展方形搜索

由于目标位置散布具有对称性，而上述扩展方形搜索方法缺乏对称性，将导致探测概率偏低，因而提出如图2所示的搜索方法，暂称为双机对称扩展方形搜索法。双机各次探测概率的计算公式与上相同，只是探测时悬停点的坐标发生了变化。

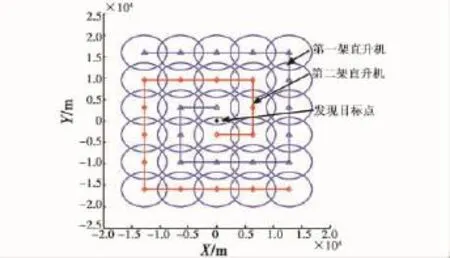
图2 双机对称扩展方形搜索示意图Fig.2 Two helicopters symmetrical extended squared search

3.3 双机搜索使用决策

反潜直升机的任务时间都是有限的，即探测次数的最大值一般是确定的。根据上述模型，可计算出不同探测次数下的搜索面积、搜潜概率与所需的搜索时间。依据这些参数，就可以根据战场态势和任务要求做出决策，如:选择搜索方法、确定探潜次数等。

4 仿真计算与分析

设t0=0时刻获知目标位于半径Rc为1 km的圆形区域内的概率p1为0.95;直升机10 min后起飞，平均飞行速度Vhel为220 km/h;吊放声纳探测半径Rd为5 km;工作深度Hw为水下150 m;κ取1.6;平均吊放速度Vdrag为3 m/s，Tlis为6 min;第一次探测时距 t0的时间Td为30 min;目标速度分布参数v0为6 kn或20 kn(1 kn=1.852 km/h)。不同探测次数下，双机搜潜概率仿真结果如图3与表1所示。

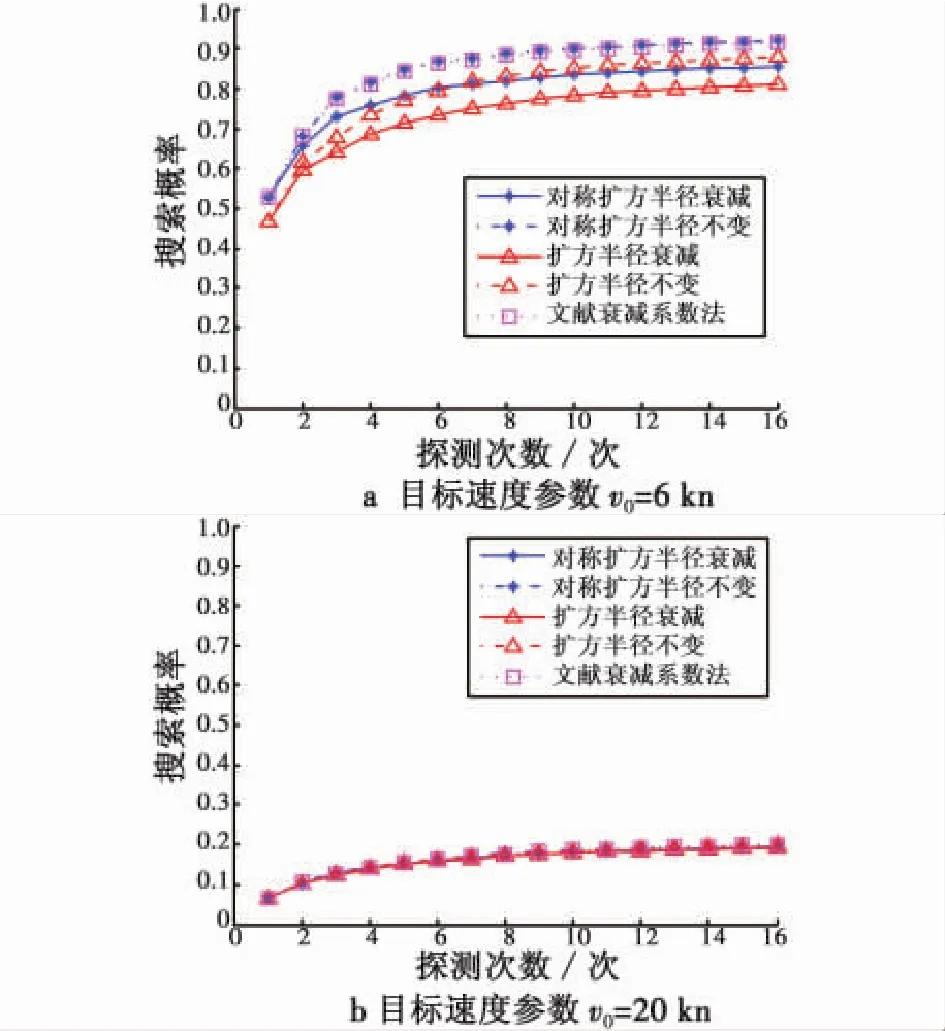
图3 不同探测次数下的任务搜索概率Fig.3 Search probalility with different detecting times

由图3a可得，当目标速度分布参数v0=6 kn时，有如下结果。

1)对称扩展方形搜索概率明显高于扩展方形。考虑已探测区半径衰减时，前者高出后者平均约8.2%;而不考虑半径衰减时，平均高出约7.6%。改变仿真参数发现，Td越小、Rd越大、v0越小，高出值越大，即对称扩展方形的优势越明显。

2)不考虑已探测区半径衰减时，搜索概率都高于考虑衰减时的。因为随着时间的推移，目标有可能会进入已探测区。因此，模型中考虑半径衰减使得计算结果更符合实际。

3)探测次数较少时，任务搜索概率随着探测次数的增加有明显提高;而探测次数较大时，增加探测次数对搜索概率的影响不大。这是因为目标散布面积增加，降低了吊放声纳单次探测的发现概率。

4)文献［3］中引入衰减系数计算得出的搜索概率一般较高，与不考虑探测半径衰减相差不大。衰减因子取不同值计算时，得出类似结果，说明引入衰减因子的效果不明显。

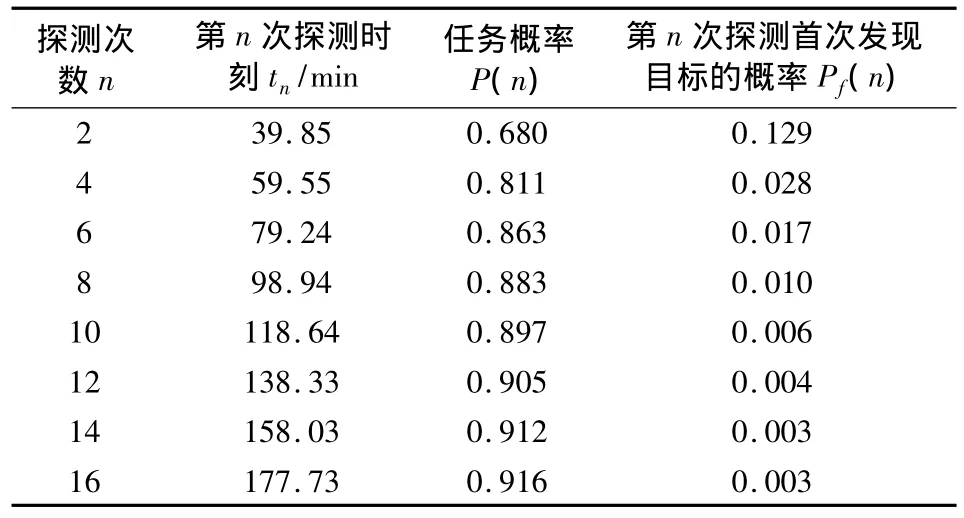
表1 双机对称扩展方形法仿真结果(半径衰减、v0=6 kn)Table 1 Simulation result of symmetrical extended squared search(radius revised，v0is 6 kn)

表1所提供的数据可作为当前参数下指挥决策的依据:1)如果要求搜潜概率达到0.9，则至少应搜索10次，直升机留空时间至少为118 min(未考虑返程与油料余量)，如果要求搜潜概率为0.95，则不能采用此搜索方法;2)首次发现目标概率随着探测次数的增加迅速减小，当探测次数超过10次时，Pf(n)已很小了，则继续搜索对搜索概率的影响很小，因而可设置一个阈值，当Pf(n)小于该值时，则终止搜索;

在目标速度分布参数v0=20 kn时，搜索概率很低，各种模型计算结果相差不大，仿真结果如图3b所示。说明对于高速目标，如核动力潜艇，两种搜索方法都难以满足搜潜要求。

仿真发现，目标初始位置精度对搜索有较大影响。对于v0=6 kn的目标，若要求搜索概率不低于0.75，不同Rc与所需探测次数的变化关系如图4所示。

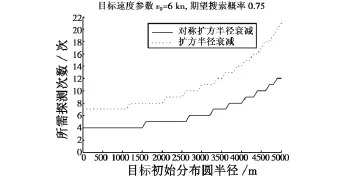
图4 Rc对所需探测次数的影响Fig.4 Effect of Rcto detecting times required

当Rc较小时，需要的探测次数也少;随着Rc的增加，探测次数也急剧增加。当前仿真参数下，对称扩展方形所需的探测次数比扩展方形的少3次以上。

5 结束语

对于速度较低的常规潜艇目标，本文提出的对称扩展方形具有比扩展方形更高的搜索概率;当指定搜潜概率时，前者所需的探测次数明显少于后者;表明对称扩展方形具有更高的搜索效能。然而，对于机动速度较高的核潜艇，两种搜索方法的发现概率都较低，难以满足反潜要求，可考虑采用其他搜索方法，或使用声纳浮标进行搜潜。当探测次数达到一定数量时，由于目标散布面积过大，继续探测对搜索概率的影响不大。本文通过修正探测概率计算模型，使得计算结果更符合实际，提高了模型的可信度。作战应用中，将实际参数带入本文的模型，则计算得出的结果对战术决策具有辅助和参考作用。

［1］孙明太.航空反潜战术［M］.北京:军事科学出版社，2003.

［2］MARTIN J.Multiplying the effectiveness of helicopter ASW sensors［J］.Sea Technology,2006,47(11):33-36.

［3］陈建勇，冷江，于传健.使用吊放声纳的直升机应召搜潜发现概率［J］.海军航空工程学院学报，2004，19(5):559-563.

［4］孙明太，赵绪明.解析法和模拟法在吊放声纳搜潜效能计算中的应用分析［J］.海军航空工程学院青岛分院学报，2004，27(3):8-14.

［5］赵绪明，孙明太.吊放声纳搜索效率模型探讨［J］.电光与控制，2005，12(2):37-41.

［6］吴芳，杨日杰.多机吊放声纳应召搜潜建模与仿真［J］.航空学报，2009，30(10):1948-1953.

［7］孙明太，王涛，赵绪明.反潜直升机吊声搜潜效能的建模仿真［J］.火力指挥与控制，2005，30(6):33-36.

［8］吴铭.多机吊放声纳检查搜潜建模与仿真研究［J］.计算机工程与设计，2010，31(3):676-679.

［9］吴福初，王磊，刘卫东.反潜直升机吊放声纳搜潜效能［J］.火力与指挥控制，2010，35(11):72-75.

［10］白晶，韩亮.舰载直升机吊声的搜潜方法探讨［J］.北京航天航空大学学报，2007，33(3):282-285.

［11］孙明太.航空反潜概论［M］.北京:国防工业出版社，1998.

［12］TRACEY P A.Search priorities for a target probability area［D］.Monterey,CA,USA:NavalPostgraduateSchool,1980.