基于概率神经网络的发动机故障诊断方法研究
朱明悦,李小申
ZHU Ming-yue1, LI Xiao-shen2
(1.河南化工职业学院,郑州 450042;2.河南科技大学 数学与统计学院,洛阳 471003)
0 引言
在传统的故障模式诊断技术中,模式分类采用的基本方法是利用判别函数来划分每个类别。然而,在很多情况下,特别是对于线性不可分的复杂决策区域,判别函数的形式也就格外复杂,而且全面的典型参考模式样本也不容易得到。神经网络作为一种自适应的模式识别技术,并不需要预先给出有关模式的经验知识和判别函数,它通过自身的学习机制自动形成所要求的决策区域。网络的特性由其拓扑结构、神经元特征、学习和训练规则决定。它可以充分利用状态信息,对来自不同状态的信息逐一进行训练而获得某种映射关系。而且网络可以连续学习,如果环境发生了变化,这种映射关系还可以自适应地进行调整。鉴于此,神经网络在故障模式识别领域的应用越来越广泛。本文提出一种径向基概率神经网络模型,用于发动机故障模式的诊断。仿真结果表明,该网络学习速度快,诊断准确率高,对样本噪声的鲁棒性强,可以对系统进行实时监测和诊断。
1 概率神经网络
概率神经网络(Probabilistic Neural Networks,PNN)是一种结构简单、训练简洁、具有较强容错能力和结构自适应能力的径向基函数(Radical Basis Function, RBF)神经网络,主要用于模式分类和故障诊断中。
1.1 概率神经网络的结构
概率神经网络是一种具有单隐层的三层前向神经网络。输入层将系统提取的特征参数直接传递给隐含层,不做任何处理,因此,输入层仅仅起到传输信号的作用,其神经元的个数与输入样本向量的维数相同。输入层和隐含层之间可以看作权值为1的连接。
隐含层也称为模式层,采用非线性优化策略,对径向基函数(通常为高斯函数)的参数进行调整,得到故障模式的估计概率密度函数。模式层神经元的个数由故障样本数据的多少决定,当故障样本的数量增加时,模式层神经元的个数也将随之增加。
输出层采用线性优化策略,是隐单元输出的线性加权和。输出层神经元的个数与故障模式数相等。输出层神经元是一种竞争神经元,它根据贝叶斯分类规则,将输入向量分到具有最大后验概率密度的类别中,即概率密度最大的神经元输出为1,其它神经元输出全为0。
随着故障先验知识的积累,概率神经网络可以不断横向扩展,故障诊断的能力将不断提高。
1.2 概率神经网络的分类过程
概率神经网络的分类过程包括以下三步:1)网络在学习和诊断之前,首先对历史数据进行处理,包括预处理和特征参数提取,以获得网络所需的诊断输入和训练样本。处理后直接送入隐含层;2)用一定数量的训练样本集对网络进行训练,得到期望输出;3)根据当前诊断输入对系统进行诊断,诊断的过程就是利用神经网络进行前向计算的过程。基于概率神经网络模式分类功能的诊断系统结构如图1所示。
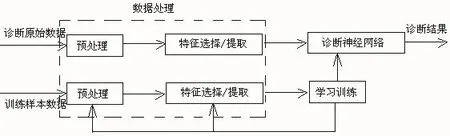
图1 概率神经网络模式分类功能的诊断系统结构
2 建立发动机故障诊断的概率神经网络模型
2.1 发动机故障诊断模型
故障模式的诊断就是根据给定的故障征兆,实现故障征兆集到故障模式集之间的非线性映射的过程。进行发动机故障诊断时,首先要从发动机瞬时转速信号提取相关的特征参数作为故障征兆,然后利用概率神经网络诊断得出故障模式。其诊断模型如图2所示。
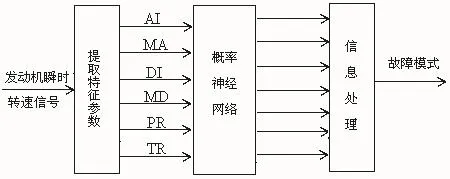
图2 基于PNN的发动机故障诊断模型
图中特征参数AI: 最大加速度指标,MA:平均加速度指标, DI:最大减速度指标,MD:平均减速度指标,PR:燃爆时上升速度,TR:扭矩谐波分量比,作为网络的输入。
2.2 故障模式的类别
发动机运行过程中,油路和气路出现故障是最多的。以发动机某一汽缸为例,这里将发动机汽缸故障分为单一故障和复合故障两大类。单一故障包括:油路故障、气门故障、汽缸故障三种模式;复合故障包括:油路—气门故障、油路—汽缸故障、气门—汽缸故障三种故障模式。考虑发动机的正常状态模式,可知发动机故障模式共有七种,分别用A(正常)、B(油路故障)、C(气门故障)、D(汽缸故障)、E(油路—气门故障)、F(油路—汽缸故障)、G(气门—汽缸故障)表示。由此可知,所设计的概率神经网络输出层应有7个神经元。
2.3 概率神经网络的拓扑结构
概率神经网络是一种单隐层的前向型神经网络,由输入层、隐含层和输出层组成。其输入层神经元个数与输入样本向量的维数相同,输出层神经元个数等于训练样本数据的总数。由以上分析可知,网络输入层神经元的个数有6个,分别对应发动机运行特征参数:AI、MA、DI、MD、PR、TR。隐含层神经元的个数由故障样本数据的多少决定。这里取12个节点,分别对应六个输入节点的故障和正常中的12种模式。输出层的神经元个数有7个,分别对应发动机汽缸的七种故障模式:A、B、C、D、E、F、G。所设计的概率神经网络的拓扑结构如图3所示。 隐含层传递函数采用高斯函数,输出层传递函数采用线性函数。
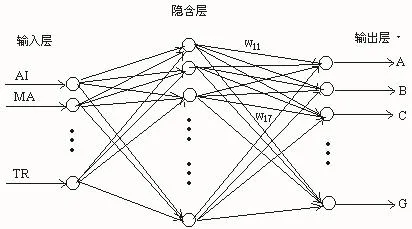
图3 PNN网络的拓扑结构
3 概率神经网络的学习过程和性能测试
3.1 概率神经网络的学习过程
无论是哪种神经网络,设计完成后,必须对其进行训练。概率神经网络的学习算法属于有导师的学习。在训练网络时,网络直接将训练样本向量存储为网络的模式样本向量,而不做任何的修改,只需对激活函数(高斯函数)的平滑因子进行经验式统计的估计。这种算法模型具有很好的推广能力,适于故障模式的识别。训练好的网络计算速度快,内存消耗低,可用于实时监测和诊断。用于网络学习的样本数据如表1所示。
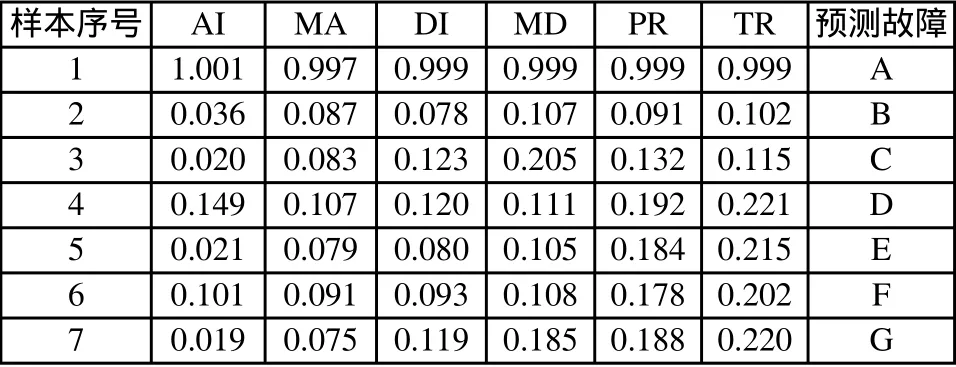
表1 网络训练样本数据
由于这些数据之间相差不大,因此,不需要进行归一化处理,可以直接对网络进行训练。
在MATLAB提供的软件环境下,应用语句:net=newpnn(P,T,Spread) 创建概率神经网络函数。其中,P为网络的输入样本向量,对应表1中的故障征兆;T为网络的目标向量,对应表1中的故障类别;Spread为径向基函数的分布密度,其默认值为0.1。Spread的取值大小,决定了网络包含的聚类区域的范围大小,对网络的性能有较大的影响。为了更好地分析Spread对网络性能的影响,仿真过程中,分别取Spread=0.1、0.2、0.3、0.4、0.5。
利用上述语句创建概率神经网络的同时,可以自动增加隐含层神经元的个数,直到均方差满足要求为止,也就是说,在用newpnn创建概率神经网络的同时,已经完成了对网络的训练。
调用以下语句检验网络在Spread 不同取值下对训练样本数据的分类情况。
for i=1:5; net=newpnn(P,T,i/10);temp=sim(net,P); yc=vec2ind(temp); end
在Spread分别取0.1、0.2、0.3、0.4、0.5时,概率神经网络都输出了同样的结果:
yc=1 2 3 4 5 6 7
以上仿真结果表明,此概率神经网络能够成功地将故障分为七种预定的故障模式。学习速度快,诊断准确率高,对Spread小范围内的变化不敏感。
3.2 概率神经网络性能测试
为了检验概率神经网络的泛化能力,运用表2中的测试样本数据对网络进行测试。
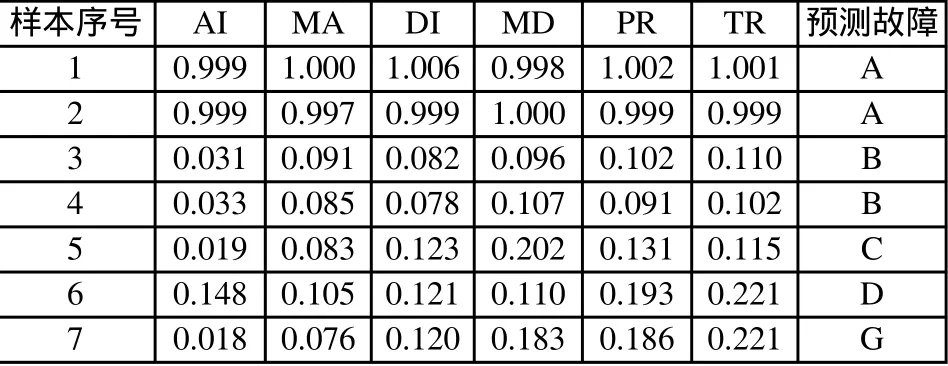
表2 网络测试样本数据
调用测试语句如下:
P_test=[ ]’; y_test=sim(net,P_test); yc_test=vec2ind(y_test);yc_test
网络输出为:
yc_test=1 1 2 2 3 4 7
网络输出结果与实际运行情况一致,该网络能够有效地对发动机故障进行诊断。
当故障样本增加时,隐含层神经元的个数也将随之增加。因此,随着故障先验知识的不断积累,网络可以不断横向扩张,故障诊断的准确度将不断提高。
4 结束语
本文基于径向基概率神经网络理论设计了一种可用于发动机故障诊断的网络模型。MATLAB实验表明,概率神经网络可以最大程度的利用故障先验知识,按照贝叶斯最小风险准则对发动机故障进行定性诊断。网络训练速度快,适于对故障的实时监控和诊断;网络泛化能力强,故障诊断准确率高;对样本噪声的鲁棒性强。概率神经网络为开发以人工神经网络为框架的故障诊断系统提供了研究的理论基础。随着神经网络技术的不断发展,概率神经网络在各种故障诊断中的应用也会越来越广泛。在一些实时性要求较高的场合,概率神经网络只需对少量的权值和阈值进行调整,网络训练速度快,诊断准确率高,易于工程实现。
[1] 张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2009.
[2] 付芹,谷立臣.PNN在旋转机械故障诊断中的应用[J].煤矿机械,2009,30(11):243-245.
[3] 谷雷,杨青,王大志.概率神经网络在化工过程故障检测中的应用[J].控制工程,2008,(5):128-130.
[4] 姬东朝,宋笔锋,易华辉.基于概率神经网络的设备故障诊断及仿真分析[J].火力与指挥控制,2009,34(1):82-85.
[5] 杨青,宋英俊.基于提升小波和PNN的三容水箱故障诊断[J].工业仪表与自动化装置,2011,(2):3-6.
[6] A.MORADKHANI,K.AHMADI,Load cell Design and Contruct with Fault Detection by Probabilistic Neural Network[C],Proceedings of 2008 IEEE international Conference on Mechatronics and Automation,2008.

