轮毂孔双键槽对称度误差测量方法研究

屈 波QU Bo

（重庆工业职业技术学院，重庆 401120）

0 引言

在工程机械中，如大型水泵、大功率减速机，其工作的额定功率较大，其输出轴若使用单键来传递扭矩，键联接的强度往往不够，若用花键来传递功率，虽可满足强度要求，但花键的制造成本较高，所以工程设计中常使用双键联接来传递较大的功率，是一种性价比较高的选择。在双键联接中，对双键键槽的对称度要求较高，如果键槽对称度的精度要求无法保证，将满足不了承载能力的需求，所以必须完善实际生产中双键对称度误差的测量方法问题。

1 轮毂孔双键键槽对称度其公差带特征分析

一般情况下，轴毂联接在采用双键传递动力时，两键在圆周方向必须是均布的，即2个键的中心平面的理想夹角为180°，图1是轮毂孔双键槽对称度的图纸标注示例。

图1 轮毂孔双键对称度公差要求的图纸标注

在此图纸标注中，对2个键槽都标注了相对于基准轴线的对称度要求，表面上看这是分别对2个键槽的中心平面提出的对称度要求，但实际上对称度公差要求从本质上说是一种位置公差要求，只不过此时2个被测键槽的中心平面的理想要素应是通过基准轴线的一个公共理想平面（笔者认为：这种公差要求如用位置度来标注能更准确地表达设计意图），双键键槽对称度的公差带应是以理想轴线为中心要素，对称布置在此中心要素两侧的2个理想平面之间的区域，如图2所示，两理想平面之间的距离为对称度公差值（图中公差值为0.04 mm）。此类公差带的位置有确定的一面，即此公差带的中心平面必须通过基准轴线，但同时，这种公差带也可以浮动，即评定键槽对称度误差值时，此公差带可绕其基准轴线转动，只要被测的2个键槽的中心平面位于此公差带内，则这2个键槽的对称度误差就符合对称度公差要求，工件此项检测就是合格的。在实际测量与评定此类双键键槽的对称度误差时，应使用定位最小包容区域来评定，其几何特性与上述对称度公差带的几何特性基本相同，不同的是此定位最小包容区域必须紧紧包容被测键槽的实际中心平面且具有最小的宽度，而此定位最小包容区域的宽度即为被测双键键槽的对称度误差值。

1.公差带边界平面；2.键槽Ⅱ的中心平面；3.公差带的对称中心平面；4.公差带的基准轴线；5.键槽Ⅰ的中心平面图2 轮毂孔双键键槽对称度公差带示意图

2 轮毂孔双键键槽对称度误差测量方法

2.1 采用的测量装置及需要测出的尺寸数据

如图3、图4 所示。在检验平板上放置一个带夹紧装置的V形架，准备一个与被测工件内孔直径尺寸相同的检验心轴安装在V形架的V形槽中，用压紧装置将其适当固定，将被测工件通过其内孔安装在上述检验心轴上，要求配合间隙最好为零，实际配合面占孔面总长的一半即可，其目的是要露出需要检测的双键键槽。然后分别组合出2组量块，量块组的尺寸分别要根据两键槽的实际尺寸j1、j2进行组合，并将这2组量块与被测键槽无间隙地装配在一起，再将一带表架的千分表放置在检验平板上，用此千分表找正工件，使安装在键槽中的量块组工作面平行于检验工作台工作面。在一般此类轮毂孔双键键槽加工中，键槽的分度并不是通过分度头进行的，而是在加工好一个键槽后，通过直接拆下插刀刀头，将其翻转180°后再次插入刀杆中夹紧，即可开始第2个键槽的加工，所以加工好的两键键槽的中心平面一般是平行的，上述工艺方法是可以保证这一点的。所以在检测中一般可同时将安装在键槽中的量块组工作面找正，使之平行于检验工作台工作面。

然后，运用相对测量法的原理，用量块校对好千分表，分别测出安装在键槽中的2组量块的上工作面到检验平板工作面的实际距离尺寸h1、h2，以及心轴相对于平板的最高素线到检验平板工作面的实际距离尺寸h3，再用内径千分表测出工件内孔的实际直径尺寸Da。

1.检验平板；2.V形架；3.心轴；4.V形架紧固装置；5.工件；6.千分表；7.量块；8.千分表调零量块组图3 测量装置示意图的主视图

2.2 数据处理及对称度误差的计算

工件轮毂孔轴线到检验平板工作面的实际距离hx= h3－Da/2

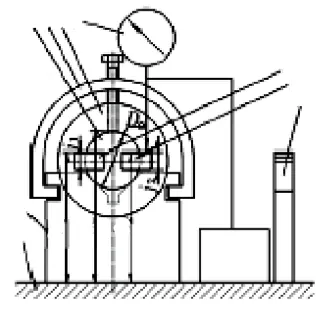
1.检验平板；2.V形架；3.心轴；4.V形架紧固装置；5.工件；6.千分表；7.Ⅰ号量块；8.Ⅱ号量块；9.千分表调零量块组图4 测量装置示意图的左视图

Ⅰ号量块中心平面到轮毂孔轴线的实际距离

b = h1－j1/2－hx

Ⅱ号量块中心平面到轮毂孔轴线的实际距离

a = h2－j2/2－hx

当计算得到的a值和b值符号相反时，说明两被测键槽的中心平面分别位于基准轴线所在的水平面的异侧，如图5所示。图中FM 线代表Ⅰ号量块的中心平面，NH线代表Ⅱ号量块的中心平面，这些平面分别模拟了两个被测键槽的实际中心平面，下面要进行对称度误差的评定，但这里涉及到一个定位最小包容区域的判别问题，需要说明：国家标准中，并未给出定位最小区域的判别法，但可以根据最小包容区域的定义做出判别，而且本文所针对的此类对称度误差的最小包容区域有一些特殊性，首先，这种对称度误差的最小包容区域相对于基准是对称的，其次，这类对称度误差最小包容区域的中心要素是一条基准轴线，即此类对称度公差是所谓面对线的对称度公差。

1.Ⅰ号量块；2.Ⅱ号量块；3.工件图5 轮毂孔双键键槽对称度误差分析与计算示意图

所以根据上述特点，如图5所示，因图中的最小包容区域的基准轴线的投影具有投影积聚性，其投影成为一点O，过O点的最小包容区域的中心平面将评定对称度误差的最小包容区域分为对称的两半， 因此只要在此最小包容区域的一半区间内，点O与2个被测要素按评定直线度误差的相间准则构成局部的最小包容区域，再以此为基础得出的整个最小包容区域的宽度就应该是最小的。

根据上述分析，可在图5中画直线l1l2，使之过FM平面的点F和NH平面的点H，点O与点F和点H就构成高、低、高相间的状态，即可构成局部的最小包容区域， 但这只是半个定位最小包容区域，然后再画直线l2，使之平行于直线l1，并使直线l2到O 点的距离等于直线l1l2到点O 的距离，因此图5 中上下2 条倾斜的直线l1、l2之间的区域就是评定对称度误差的定位最小包容区域。当然，除此之外还有一种画l1的可能，就是过点N和点M画线，点N和点M 和点O构成高、低、高相间的状态，但很明显由此形成的包容区域并不能完全包容被测键槽的实际中心平面，故不能采用。

所以，评定对称度误差的定位最小包容区域应如图5所示，直线l1、l2代表包容被测键槽实际中心平面的极限包容面，竖直中心线与直线l1的交点为点P，过圆心点O的EK线为此定位最小包容区域的宽度，因此只要求出EK 线的长度即可求得此种情况下两键槽的对称度误差，但图中EK线的长度求解比较困难，而实际测量时直线l1倾斜角一般很小，在简化计算而又能保持一定的测量精度前提下，可得OE≈OP，EK 线的长度约等于2倍的OP，而OP线的长度可按下面的方法求出：

因为△FDC ∽△HGC ∽△OPC

有

而FD＝b、GH=a

所以式（1） 变为

则OP=a OC/GC

又从图5 中的几何关系可知OC+GC=R+h

则

将式（4）代入式（3），则

再从图5 中的几何关系可知DC≈OC+R而根据式（1）可知DC=b GC/a

所以可得b

再将式（ 4）代入式（6） ，可得

再将式（7）代入式（5），可得

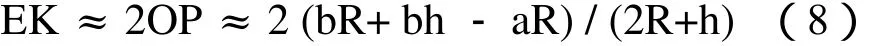
所以，最后式（8）变为

由于上述推导过程中没有考虑各参数的正负号，考虑到可能出现|b|＜|a|的情况，为使公式更具普遍适用性，式（9）可变为

3 结束语

1）本文论述了在使用通用计量器具的条件下检验轮毂孔双键键槽对称度误差的方法，并给出了具体情况下计算其对称度误差值的理论公式， 在工程实践中对此类零件的相关检测具有一定的指导作用。

2）本测量方法推导时忽略了键槽长度方向的位置误差对对称度误差的影响，这是因为此种误差易被工艺控制，一般来说误差值极小。

3）本方法在测量开始阶段，必须调整、找平工件的键槽中心平面，较耗费时间，也需要一定的技能，所以一般较适合首检或小批生产的场合。

[1] 赵小明, 张武坤. 双键对称度误差的测量与计算[J]. 现代制造工程, 2005(2): 107-108.

[2] 刘庆胜, 赵文广. 国家标准中的轴键槽对称度误差计算公式的推导[J]. 工具技术, 2008(11): 107-109.

[3] 弓立明. 轧辊双键槽对称度的测量[J]. 工具技术,2003(9): 61.