基于运行状态信息融合的电站制粉系统实时优化研究

朱龙彪，王 恒，贾民平，陈左亮

（1.南通大学 机械工程学院，南通 226019；2.东南大学 机械工程学院，南京 211189；3.大唐南京下关发电厂，南京 210011）

0 引言

在我国，球磨机制粉系统是火电厂主要的辅助系统。对于中间仓储式制粉系统，火力发电厂厂用电占电厂总发电量的10%左右，而制粉系统约占厂用电的15%～20%，是电厂的耗电大户之一，也是潜在的节能大户[1～3]。降低制粉系统的能耗，实现经济优化运行，对于电厂降低成本、提高竞争力具有重要的意义。由于制粉系统具有非线性、时变性和强耦合的特点，同时由于受到测量手段的局限，一些工艺参数(如料位、煤粉细度)难以在线直接测量，导致了用常规的机理模型来进行系统优化具有一定的局限性。

球磨机制粉系统优化的方法一般是根据电厂制粉系统的实际情况，设计和安排系统优化试验，通过试验来确定制粉系统的最佳工作点和最佳运行方式[4,5]。这种优化方法多是基于试验基础上的区间优化或结构参数的调整，一般可以根据实际情况对制粉系统进行优化调整，指导实际运行。但是，需要做大量的试验、成本高、工作量大、实验数据分散，同时该方法并且没有形成具有定量和适合于自动控制的参数化工况，使得系统的优化和自动控制是相互独立的。

随着人工智能技术的发展，目前文献出中已有基于建模法来对热工系统进行优化[6～8]，其基本思路是依据系统的过程特性与生产过程中的技术要求、限制条件和安全性等，抽象出具体的数学模型，包括目标函数、约束条件，在数学模型的基础上，采用适当的优化算法进行系统的优化求解，以获得热工系统的优化运行参数，指导运行人员的操作。但是上述算法中的模型都是离线得到的，并不适合在线建模和实时优化。所谓实时优化，就是指根据所得到的各种信息，利用计算机自动地周期性地完成优化计算，并将最优参数值直接送到控制器作为设定。事实上，由于电厂DCS系统或专用的实时数据库中保存了机组运行时所有必要的实时数据，这些数据反映了机组的运行状态信息，利用这些实时数据，并通过非线性在线建模技术，就能得到制粉单耗与当前运行工况之间的数学关系。

针对目前制粉系统优化方法的不足，本文基于在线神经网络建模算法，建立了制粉单耗与各种影响因素之间的非线性模型，并结合遗传算法对上述模型进行寻优，获得可控变量参数的优化值，为实现系统优化控制奠定了基础。

1 球磨机制粉系统的优化目标

球磨机制粉系统的优化目标是在保证系统安全稳定运行的基础上、在满足锅炉燃烧煤粉细度的前提下，使球磨机运行在高出力工况下，使得制粉单耗尽可能降低。

球磨机消耗的电网功率按下式计算[9]：

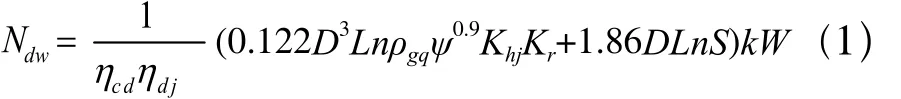
式中，ηcd—电动机至球磨机的传动效率，一般可取为0.885；

ηdj—电动机效率，取为0.92；

Kr—考虑燃料性质的系数，与燃料种类和钢球充满系数有关，对无烟煤Kr=0.95，其他的煤Kr =1.05，筒中无煤时Kr=1.0；

S—筒体和护甲的总厚度(波浪型护甲按波的中心线计算)，一般有S=D/40。

根据磨煤出力和消耗的电网功率，可以确定磨煤单耗为：

由于给煤机电耗占制粉系统总电耗的比重很小，而且几乎不随系统调整而变化，一般情况下不考虑给煤机的电耗。因此，整个制粉系统的电耗主要包括球磨机电耗和排粉机电耗两部分，即：制粉系统总电耗：Ps=Pdw+Ptf，则制粉单耗Es为：

式中，Em—磨煤单耗，KWh/t；Etf——通风单耗，KWh/t。

由式(1)可知，钢球磨煤机磨煤时的功率消耗与无煤空载功率消耗相差无几。在正常的钢球装载系数范围之内，磨煤功率消耗只比空载运行增加5%[9]。这是因为球磨机运动部分(带护甲的筒体和钢球)的质量要比其中的燃料大许多倍，绝大部分能量消耗在转动筒体和提升钢球上。由此可知，球磨机的磨煤功率与磨煤出力无关，而磨煤的单位电耗随出力的增加而降低。因此，为了提高球磨机的运行经济性，通常要求球磨机在高出力下运行。

由式(3)可见，制粉单耗所包含的磨煤单耗和排粉单耗都与球磨机的出力有关，提高制粉出力不仅可以降低磨煤单耗，也可以有效降低排粉单耗，从而降低制粉单耗，是实现制粉系统系统优化的关键所在。因此，可将球磨机制粉系统优化问题转化为单目标优化问题，即在保证安全运行的基础上，如何调整制粉系统的运行参数，使得制粉单耗降低。

2 制粉单耗在线监测模型的建立

2.1 资源优化网络算法

人工神经网络模型具有很强的非线性映射能力、自学习适应能力、联想记忆能力、并行信息处理能力及容错能力，这些特点使神经网络非常适合于复杂系统的建模与控制，特别是当系统存在不确定性因素时，更体现了神经网络方法的优越性。神经网络离线建模技术在实际中已经得到了较多的应用，目前在线建模方法也得到了越来越多的重视。Platt提出的资源分配网络(Resource Allocating Network, RAN)[10]是典型的RBF神经网络在线学习算法。V Kadirkamanathan和M Niranjan从函数空间的角度对RAN方法进行了描述，并采用扩展卡尔曼滤波器 (Extended Kalman Filter, EKF)算法[11]代替LMS算法调整网络参数，改进了RAN方法的收敛速度，并可以降低网络的复杂性，且在函数逼近和时间序列预测方面的性能明显优于RAN方法，所得到的网络称为RAN-EKF。Lu针对RAN中隐节点数只增不减的缺点，提出了隐节点数可以按一定要求减少的最小资源分配网络(Minimum RAN,MRAN)[12]。MRAN除满足距离准则和误差准则外，当前网络对过去多个样本偏差都过大时，才增加新隐节点；某隐节点对多个连续输入的样本不被激活后就删除该节点。

RAN、RAN-EKF和MRAN可以实现在线学习，但这些方法存中，隐节点一旦添加就不能删除。在线学习的情况下，随着学习时间的增加，网络的隐节点将越来越多，其中相当一部分隐节点可能是无用的或冗余的。根据神经网络泛化理论，在满足学习精度的情况下，网络的规模越大，不仅会浪费系统资源，更会导致泛化能力变差。MRAN对隐节点的删除做了简单处理，但存在误删隐节点的可能性。此外，由于RAN、RANEKF和MRAN只用最新的单个样本训练网络，容易陷入局部最优，且抗劣质样本能力较差。另外，在数据中心调节过程中，部分数据中心的位置可能与网络中其他数据中心趋于重合，还有部分数据中心可能移出正常工作区域，这都将浪费系统资源并影响网络的泛化能力。

因此，比较合理的在线建模方法是在学习过程中使用最近的多个样本，并动态调节网络参数：在当前网络对样本偏差过大时在线生成隐节点；当偏差较小时，调节数据中心、输出权值和偏移，消除误差；当网络中产生重合的隐节点时，合并冗余的节点；删除对多个连续输入的样本不被激活的隐节点。基于上述思想，魏海坤提出了一种RBF网络在线建模算法—资源优化网络(Resource Optimized Network, RON)[13,14]，本文基于RON算法对制粉单耗进行在线建模与监测。

2.2 制粉单耗在线监测模型的结构

制粉单耗的影响因素有很多，其与球磨机出力、筒内料位、钢球装载量、钢球直径及配比、系统通风量、粗粉分离器折向门开度、煤种及煤质等诸多因素相关。这些影响因素归纳起来可以分为两类，即设备参数和运行参数。设备参数主要是指钢球装载量、钢球直径配比、煤种和粗粉分离器挡板开度等设备相关参数，这些参数在运行时基本不会发生改变或者是随时间缓慢变化；运行参数主要是指进出口压差、磨电流、出口温度等实时参数，这些参数直接反映了球磨机当前的运行状况。

在煤种稳定的情况下，原煤水分和可磨性系数的变化对制粉单耗的影响不是主要因素，可以忽略这些因素的影响；现场实际运行中，当煤粉细度满足要求时，粗粉分离器折向门开度一般维持在某个固定值，不需要经常变动；钢球装载量和直径配比是慢时变过程，通过对球磨机电流的监测，定期补充一定数量的钢球，可以基本维持不变，钢球装载量变化的影响可以不予考虑。因此，在上述影响因素稳定或者忽略不计的情况下，制粉单耗的主要影响因素归结为球磨机出力、系统通风量和料位。

综上所述，采用球磨机出口温度反映煤粉干燥能力，用给煤量、球磨机电流表征磨煤能力，用筒体振动有效值、进出口压差反映筒内料位的变化，用球磨机入口负压和排粉机电流来反映系统的通风量。因此，选取球磨机电流、筒体振动信号、排粉机电流、球磨机出口温度、入口负压﹑进出口压差和给煤量这7个过程参数作为资源优化网络模型的输入变量，将制粉单耗作为模型的输出变量，制粉单耗在线监测模型结构如图1所示。该模型反映了系统当前工况与制粉单耗之间的非线性映射关系。

图1 制粉单耗在线监测模型结构

2.3 数据样本的获取

为了获取制粉单耗建模的数据样本，以某电厂135MW机组球磨机系统作为试验对象，进行制粉出力全负荷的测试试验。其中，球磨机筒体振动信号由现场同步采集，采集方法可参见文献[15]，其他工艺量数据由电厂DCS系统的工程师站获得。实验开始时，调整现场采集计算机时间，使其与DCS系统时间保持一致。最后，将同一时刻采集的筒体振动数据和其余工艺量数据作为一组样本，制粉单耗离线计算求得。试验中球磨机的相关参数如表1所示。

表1 球磨机相关参数

2.4 建模结果与分析

选取给煤量为45t/h的工况下所获得的试验样本数据50组，前40组数据作为神经网络的训练样本，后10组数据用来验证模型的泛化能力。在建模之前，输入、输出数据都进行归一化处理。

RON 算法的参数选择为：γ =0.97，L=10，εmin=0.001，δmax=18，δmin=1，κ=0.3，η=0.5，Cmax=100，max Epoch=200，Δcmin=Δrmin=0.01。模型计算结果如表2所示。

由表2可见，对于验证样本，RON建模结果的最大相对误差为0.33%，建模的精度非常高。因此，可以认为建立的神经网络模型具有良好的泛化能力。

表2 制粉单耗实际值与模型值的比较

为了便于比较，在Matlab运行环境下，给出RON算法与RBF网络离线学习的正交最小二乘法算法(Orthogonal Least Square algorithm, OLS)、资源分配网络算法(RAN)的辨识结果比较，定义性能指标PER如式(4)，比较结果如表3所示。

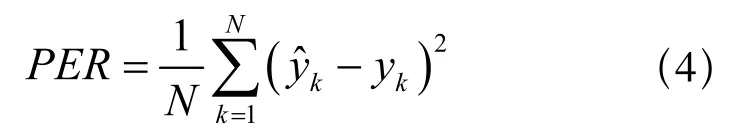
表3 几种算法的辨识结果比较

由表3可见，无论是训练误差还是最终的隐节点RON都要优于RAN和OLS算法。在获得较高建模精度的同时，也获得了优化的网络结构。尽管CPU运行时间上，RON算法要慢于OLS和RAN算法，但是由于球磨机系统对象时间常数比较长、惯性较大，故RON的运算速度是可以满足工程实际建模需要的。

3 基于遗传算法的球磨机系统的优化

应用已训练好的制粉单耗模型来优化球磨机系统是从输出到输入，即求取在给定条件下当制粉单耗达最小时，各输入参数所对应的工况。因此，球磨机系统优化的问题转化成给定条件下使得目标函数制粉单耗最小的优化问题，优化参数采用决策模型中所选取的7个参数。在保证球磨机系统安全运行的前提下，同时兼顾现有的运行情况和设备状况，每一个优化参数都有一定的运行范围，这样就构成了优化的约束条件。设优化参数为Xi(i=1,2,…,7)，每一个参数范围设定为[ai,bi]。

综上所述，球磨机系统优化问题可以描述为：

式中，Es为制粉单耗（KWh/t），f表示已训练好的神经网络所建立的非线性映射关 系；Xi(i=1,2,…,7)为优化参数，[ai,bi]是每个优化参数所对应的约束条件。

在对球磨机系统进行不同工况测试的基础上，对已建立的制粉单耗优化模型利用遗传算法进行寻优。遗传算法优化的主要步骤如下：

1） 参数编码

在研究的实际问题中，需要寻优的参数就是神经网络模型的7个输入量，同时分别对待寻优参数进行范围限制，以保证系统在有效的范围内寻求最优参数或次优参数，采用固定长度的二进制编码的方式。

2 ）初始群体的设定

根据先验知识对参数的取值进行限制，然后在满足这些要求的解中随机选取，即待寻优参数范围的确定是参数的合理范围，初始种群从该范围内随机选取。用这种方式产生初始种群可使遗传算法更快地到达最优解。

3） 适应度函数的设计

适应度函数是根据目标函数确定的用于区分群体中个体好坏的标准，是算法演化过程的驱动力，也是进行自然选择的惟一标准。球磨机系统优化的目标是寻求最优运行参数值，使得制粉单耗最小，这是目标函数最小化问题。因此，适应度函数可以直接取为制粉单耗，即

4）遗传操作

图2 制粉单耗遗传算法寻优过程

遗传操作主要包括选择、交叉和变异。选择运算采用比例选择算子、交叉运算采用单点交叉算子、变异运算采用基本变异算子。

5）算法控制参数的设定

遗传参数设置: 遗传代数G=200，群体规模N=100，交叉概率Pc=0.6，突变概率Pm=0.10。

制粉单耗遗传算法寻优过程如图2所示。由遗传算法优化优化得到的结果如表4所示（只列出可控参数）。同时为了便于比较，表4中列出了试验中获得的制粉单耗最小的实际工况参数。

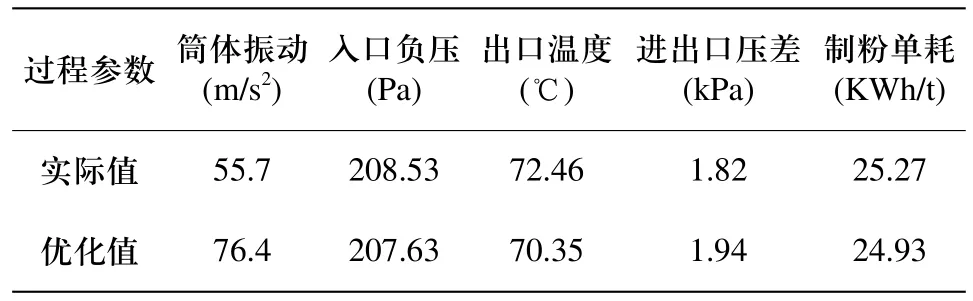
表4 遗传算法优化结果

由表4可见，通过遗传算法优化得到的制粉单耗比实际运行中的最小制粉单耗低0.34 KWh/t。经计算，优化后的制粉单耗比测试试验中的平均单耗低0.84KWh/t,此机组年耗煤量为40万吨，上网电价为0.38元/千瓦时，则年效益可增加：

ΔP=4×105×0.38×0.84=127,680（元）

4 结论

针对目前制粉系统优化算法的不足，引入神经网络非线性在线建模技术，提出了一种基于改进资源分配网络算法的球磨机系统在线优化算法。基于资源分配网络算法获得制粉单耗与过程参数之间的非线性映射关系，在此基础上，建立起球磨机系统在线监测模型，并利用遗传算法对决策模型进行寻优，获得优化运行参数。优化结果表明，该算法能有效地降低制粉单耗，较之传统优化算法更为简单实用，并且获得料位、入口负压和出口温度等可控变量参数的优化值，为实现系统优化控制奠定了基础。

[1] Peltier R.Coal plants work to stay competitive, compliant[J].Power, 2003, 147(1): 35-45.

[2] Leonard G.Austin, Heechan Cho.An alternative method for programming mill models[J].PowerTechnology, 2002,122(2-3): 96–100.

[3] M.A.Van Nierop, M.H.Moys.Exploration of mill power modeled as function of load behaviour[J].Minerals Engineering, 2001, 14(10): 1267-1276.

[4] 周名亮.300MW机组中储式制粉系统优化运行的试验研究[J].上海电力学院学报, 2006, 22(3): 217-220.

[5] 吴东垠, 盛宏至, 魏小林, 等.燃煤锅炉制粉系统的优化运行试验[J].中国电机工程学报, 2004, 24(12): 218-221.

[6] 罗子湛, 何祖威.基于系统辨识的中储式制粉系统的运行优化[J].重庆大学报, 2005, 28(1): 60-64.

[7] 刘定平, 肖蔚然, 陆继东.基于煤粉细度反馈控制的制粉系统优化[J].华南理工大学学报, 2007, 35(6):34-37.

[8] 禤莉明,卓小芳,何祖威.基于遗传算法的火电机组制粉系统运行优化[J].系统仿真学报,2007,19(1): 156-158.

[9] 范从振.锅炉原理[M].北京: 中国电力出版社, 1985: 48-62

[10] Platt J.A resource allocating network for function interpolation[J].Neural Computa, 1991(3): 213-225.

[11] Kadirkamanathan V, Niranjan M.A function estimation approach to sequential learning with neural network[J].Neural Computa, 1993(5): 954-975.

[12] Lu Y, Sundararajan N, Saratchandran P.Analysis of minimal radical basis function neural network algorithm for real-time identif i cation of nonlinear dynamic system [J].IEEE Proc.Control Appl., 2000, 147(4): 476-484.

[13] 魏海坤, 徐嗣鑫, 宋文忠.基于RBF网络的火电机组实时成本在线建模方法[J].中国电机工程学报, 2004, 24(7):246-252.

[14] 魏海坤, 丁维明, 宋文忠, 等.RBF网的动态设计方法[J].控制理论与应用, 2002, 19(5): 673-680.

[15] Peng Huang, Minping Jia, Binglin Zhong.Investigation on measuring the fill level of an industrial ball mill based on the vibration characteristics of the mill shell[J].Minerals Engineering,2009, 22(14): 1200-1208.