A*算法在游戏寻路中的应用

胡正红，张俊花

(太原师范学院计算机系，山西 太原 030012)

随着科技的发展，人工智能技术应用在许多游戏开发过程中以提高游戏的可玩性。路径探索是游戏开发过程中经常遇到的问题，通常可以采用广度优先搜索算法或深度优先搜索算法来实现路径搜索，但这些常用搜索算法在“连连看”游戏寻路中存在数据冗余、运行时间长的缺点。针对该游戏路径搜索的特点，首先我们对常见的广度优先搜索算法进行详细分析与研究，结合游戏中的应用情况，研究A* 搜索算法和启发式搜索技术，设计估价函数，改进A*算法用于游戏寻路。

1 广度优先搜索算法在游戏中的应用

“连连看”游戏规则是:在有限的时间内，将图案相同的两张牌用三根以内的直线连在一起就可以消除，只要把所有的图案全部消完即可获得胜利［1］。

采用广度优先搜索，将目标函数修改为从一个点到另一个点的转弯次数，首先把图形Start (x1，y1)压入队列。然后扩展图形Start(x1，y1)可以直线到达的节点，用集合S0=Find(x1，y1)表示这些节点都可通过转弯数为0的路径到达，如果图形Target(x2，y2)包含在集合S0 中，结束搜索。

否则，继续扩展集合S0 中空格可以直线到达的节点，用集合S1={Find(p)|p∈S0}表示，令S1’=S1－S0(S1 包含了S0)，表示S1’中的节点和图形Start(x1，y1)之间可以通过转弯数目为1的路径连起来。如果图形B(x2，y2)在S1’中，则图形S，T 之间可以用转弯数目为1的路径连接，结束搜索。

否则，继续展开S1’集合中的空格可以直线到达的节点，用集合S2=Find{Find(p)|p∈S1’}表示，令S2’=S2－S0－S1=S2－S0－S1’(S2 包含了S0和S1)，集合S2’是图形A(x1，y1)可以通过转弯数目为2的路径到达的格子。如果图形T(x2，y2)在集合S2’中，则图形A，B 之间可以用转弯数目为2的路径连接，否则图形A，B 之间不能通过转弯小于3的路径连接。

2 A*算法的估价函数设计

A*算法具备很多优点。首先，如果起点和终点之间存在有效路径，A* 就一定能够找到;其次，只要H(n)是可纳的，它就一定能找到一条最短路径;第三，A*算法是启发式搜索算法中搜索状态最少的一种算法，它使启发式函数得到了最有效的应用［2］。

启发式搜索的核心是估价函数F(n)，“连连看”中连线不能从尚未消去的图案上经过，节点只能在四个方向移动，两个相同图案之间的连线不能超过两个弯。

因此估价函数中，需要考虑当前格Current 到目标格Target的移动耗费，当前格Current 与开始格Start的转弯数，用估价函数表示为［3］:

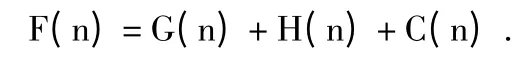
在“连连看”游戏中，格子S的移动方向分水平上、水平下、竖直上、竖直下四个方向，每个格子对应着有图案、无图案两种状态。

设计二维数组map［Rows］［Cols］表示对应的方格是否有图状态，当数组元素值取1 表示该位置有图，取0 表示无图。

估价函数F(n)的取值设定:

G(n):移动的距离。结合游戏的要求，这里设定沿着四个方向移动，移动位置上有图则距离值为无穷大，这样的格子不考虑扩展，如果无图距离值为1，如图1所示。

图1 G值的设定

H(n):指定格子到目标格横向走的步数与纵向走的步数和;例如T(Tx，Ty)是终点，C(Cx，Cy)是当前点，则:h(n)=|Tx－Cx|+ |Ty－Cy|。

C(n):起点Start 到指定格子的转弯数，直线连接C 取值为0，转一次弯，C值为1;转两次弯，C值为2;转弯数为3，估价函数无穷大。

例如:开始点S 与终点T 在一条横线上，周围的格子状态如图1所示;计算S 点的四方向节点的F(n)，上方和左方的节点估价函数无穷大，右方节点的f(n)=1+3+0，下方节点的f(n)=1+5+0;计算过程如图2－图4所示。

图2 初始状态

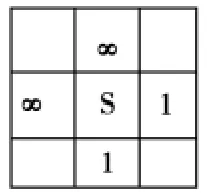
图3 G值的计算

图4 H值的计算

展开右方F值=4的点，计算其右节点估价函数f=4+(1+2+0)=7，如图5所示。

展开F值=7的节点，计算出其右节点估价函数f=7+(1+1+0)=9，如图6所示。

展开F=9的节点，终点就在它的展开节点中了，完成了最短路径工作。

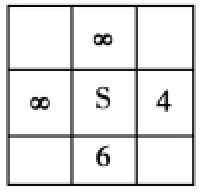
图5 估价表示

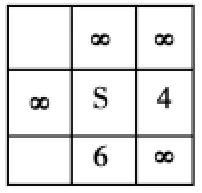
图6 展开f=4的节点

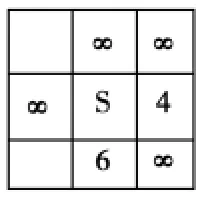
图7 展开f=7的节点

3 A*算法的应用设计

A*算法是一种典型的启发式搜索算法，它除了利用上述的启发函数来对搜索过程中的每一个节点进行评估，另外它还必须有两个表:Open 表和Close 表［4］。

Open 表由未考察的结点组成，保存了打开节点的F值;每次从Open 表中取F值最小的节点展开后续节点。

Close 表由已考察的结点组成，将已展开的节点加入其中(不包括终点)。

结合“连连看”的要求，A*算法实现的过程可以用伪代码描述，假设起始节点为Start，目标节点为Target，其中Current是每次被考察的节点，临时节点Temp 代表Current的四方向上的有效子结点，所谓有效子结点就是指在“连连看”中没有图案的格子。当Current 等于Target 时搜索成功。

A*算法作为“连连看”中的寻路算法，用伪代码表示如下:

4 A*算法在“连连看”中的应用

4.1 数字化运动方向

A*算法的数据结构设置，程序设计有其一定的模式，这里针对“连连看”，给出A*算法的实现代码。

“连连看”中节点的运动方向是4个，可以设置一个常量数组，把每个方向的移动坐标变动量存入数组，定义类的方法，传入参数:起始点坐标和目标点坐标:

图8 数字化方向

4.2 计算转弯

“连连看”中计算节点的转弯数很关键，因此定义类方法GetCrossing，传递节点的ID 号，返回起点到节点的转弯数。

4.3 寻路设计

展开节点后，定义类方法FindPath 传递相关参数计算节点坐标，记录节点ID 号，增加节点到OpenList，计算G、H、E、F值，然后把展开的节点加入到whichNode 中。

5 算法分析

假设游戏地图n 行m 列，设N=m* n，由于每个节点做为扩展节点进入Open 表最多一次，因此Open 表中最多处理N个展开节点。扩展每个节点需要O(1)的时间，因此算法最多耗时O(N)。构造相应的最短路径需要O(L)的时间，L是最短路径的长度。当节点数为N 时，广度优先搜索算法的复杂度为O(N* N)，A*算法的复杂度为O(N+L)，计算量不会随着节点的展开迅速增加，只要起点和终点之间存在有效路径，A*算法就能够快速找到。

6 总结

本文将A*算法应用在“连连看”游戏寻路搜索上，给出了改进的估价函数、算法运行流程，能够用O(N+L)的时间完成最短路径搜索，很好地适应游戏的要求。A*算法结合了启发式方法和形式化方法，为许多即时战略游戏所用到，可以修改方向参数，对于游戏中八方向移动搜索路径也具有一定的实际应用价值。

［1］胡正红.一种寻路算法在游戏中的应用［J］.山西电子技术，2009(6):53－54.

［2］陈和平，张前哨.A算法在游戏地图寻径中的应用与实现［J］.计算机应用与软件，2005(12):118－120.

［3］Hu zhenhong，Jinli.Application and Implementation of A* Algorithm in Picture Matching Path－finding［G］.In:2010 International Conference on Computer Application and System Modeling(ICCASM 2010)，Taiyuan，China，2010:224－227.

［4］陈炼，邓少波，万芳.A算法在梵塔问题中的应用［J］.计算机工程，2005(4):168－170.