大坝施工期应力应变监测资料分析

曾 超

（武汉大学水利水电学院，湖北 武汉 430072）

0 引言

某水电站由大坝枢纽、引水系统和厂区枢纽三部分组成。大坝为混凝土双曲拱坝，坝顶高程578.70 m，最大坝高108.7 m。拱冠梁上下游坝面采用两条抛物线，坝顶宽5.5 m，坝顶轴线弧长276.695 m，装机容量为2×64.5 MW。

坝内布置有安全监测系统，监测项目包括渗流、变形、应力应变和环境量监测。大坝分为16个坝段，混凝土应力状态采用5向应变计组监测，25组应变计主要布置在拱冠梁附近的8号坝段473 m、506 m、530 m、560 m高程以及506 m、530 m、560 m高程两坝肩部位，其中8号坝段位于主河道基础最深部位，被确定为标准观测断面，共埋设11组应变计，详见图1。

主要对8号坝段应力应变进行系统分析，并对该坝段应力应变监测性态进行评价。

1 混凝土应变常规分析

1.1 线膨胀系数计算

无应力计测值代表了测点混凝土的自由体积变形ε0，ε0包含三部分变形，即温度变形、自生体积变形G(t)和湿度变形εw，即：

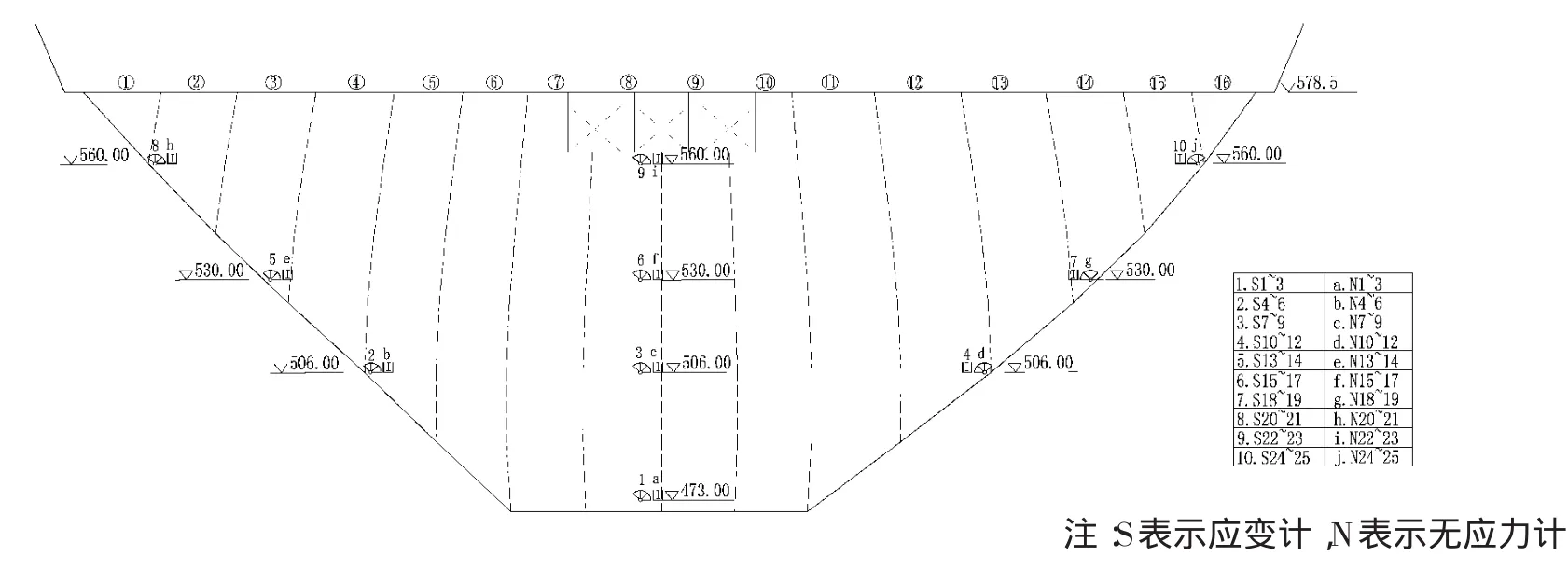
图1 五向应变计组和无应力计布置图Fig.1 Distribution of the 5-d stain meters and the stress-free strain meters on the dam

常规的线膨胀系数的计算方法是将无应力计应变测值和温度测值绘制成过程线，在这一曲线上取降温段短时间间隔的应变变化Δε0和相应的温度变化ΔT0，假定ΔG(t)+εw≈ 0，计算得温度膨胀系数为：α=Δε0/ΔT0。但该方法计算得到的温度膨胀系数误差较大，故采用线性回归方法建立统计模型得到该系数，结果表明基本符合工程实况。

在充分考虑有关影响因子后，建立自由体积变形的统计模型为：ε0=f(ΔT,τ)，其中 ΔT 为测值与基准值的温差，τ为时效因子。温差的回归系数可认为是该部位混凝土的最接近温度膨胀系数的近似值。

以8号坝段N2无应力计为例建立逐步回归统计模型为：Y=-3.606+5.769X1+1.099X2，复相关系数R=0.9412，表明模型基本能反映自由体积变形变化规律。式中X1为测值与基准温度的温度差，X2为ln(t+1)，t为观测日期减基准日期得到的日序，统计成果见表1。

根据表1，去掉最大和最小者，算得坝体混凝土综合线膨胀系数为5.57×10-6（1/℃），与室内试验值（5.7～6.0）×10-6（1/℃）接近。

1.2 自生体积变形

结合式（1）和差阻式应变计应力计计算公式，忽略湿度变化，可得出混凝土自生体积变形为：Gt=f ΔZ+(b-α)ΔT 。8号坝段混凝土自生体积变形特征值计算成果见表2。

混凝土自生体积变形的膨胀特性对增大压应力有利，反之会增大拉应力。自生体积变形在混凝土浇筑初期变化较大，随着混凝土龄期增加，自生体积变形趋于稳定。从统计成果看，坝体自生体积变形大多呈膨胀变形，有利于改善混凝土内部的应力状况。

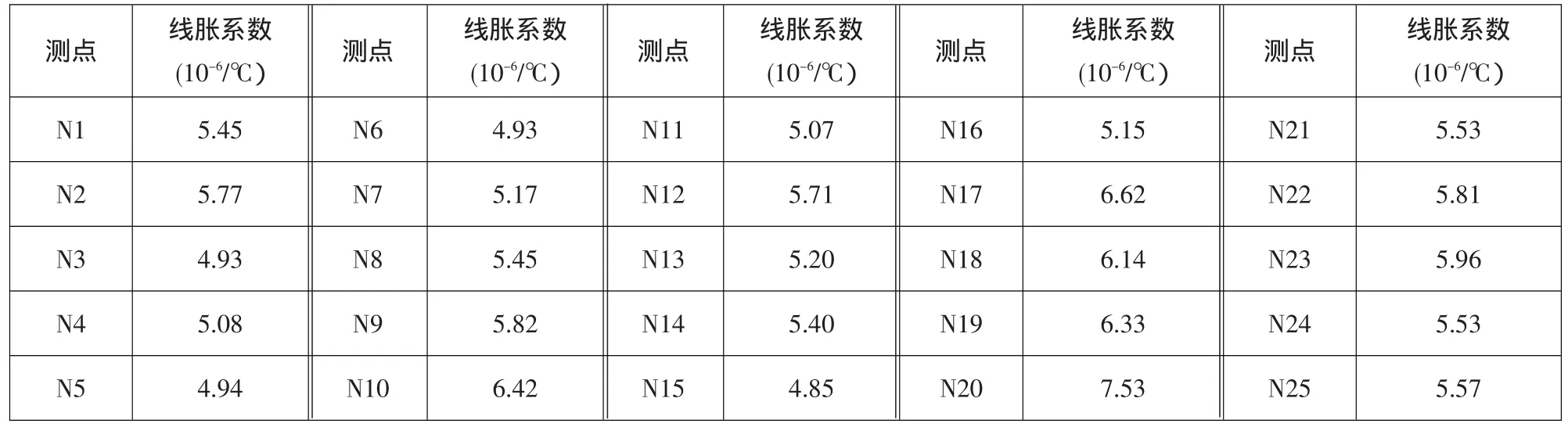
表1 混凝土线膨胀系数计算成果表Table 1 :Statistics of linear expansion coefficient

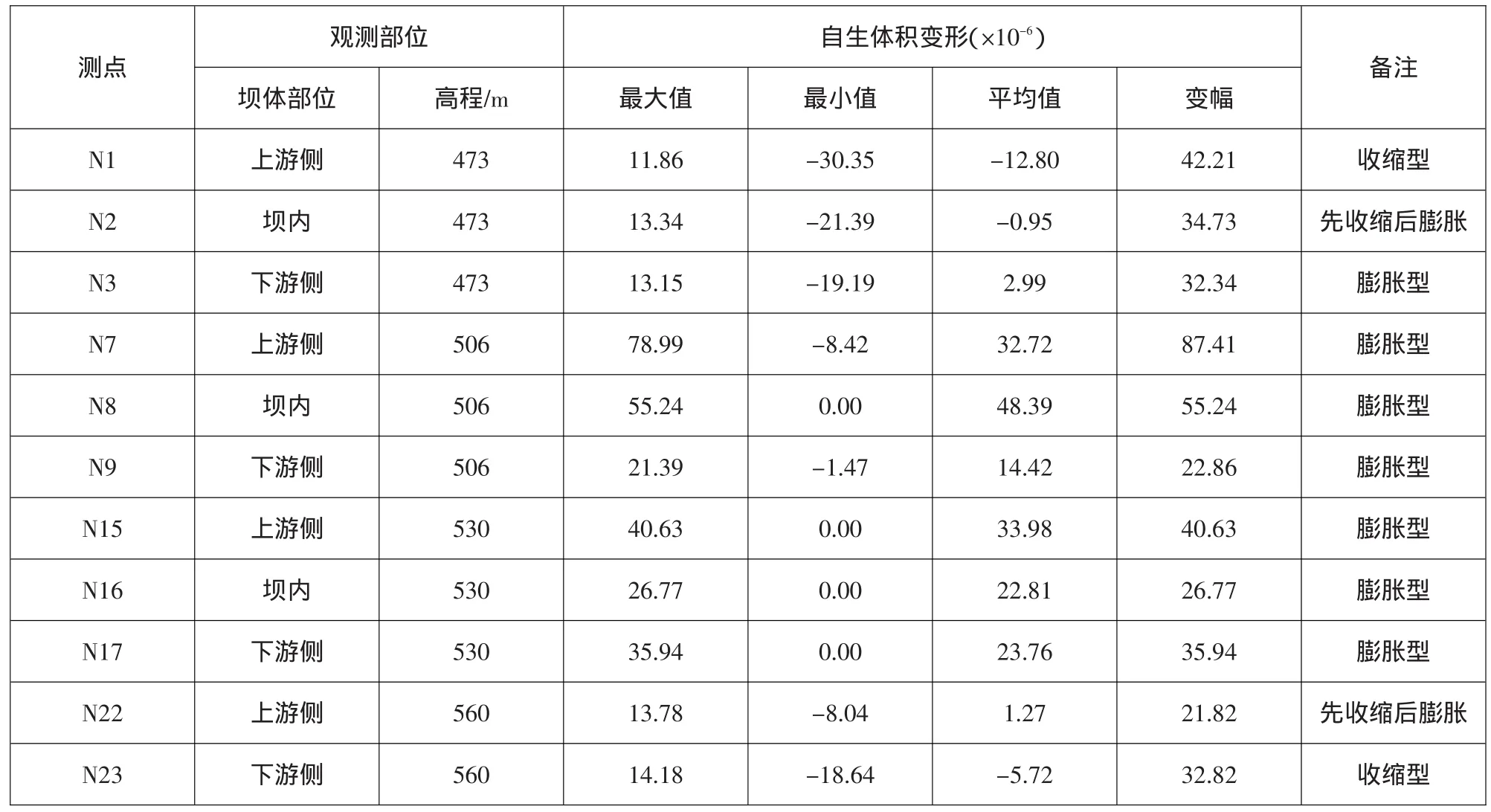
表2 8号坝段混凝土自生体积变形特征值统计表Table 2 :Statistics of the concrete autogenous volume deformation on the eighth dam block

1.3 单轴应变计算

坝内埋设的差阻式五向应变计组布置如图2所示。

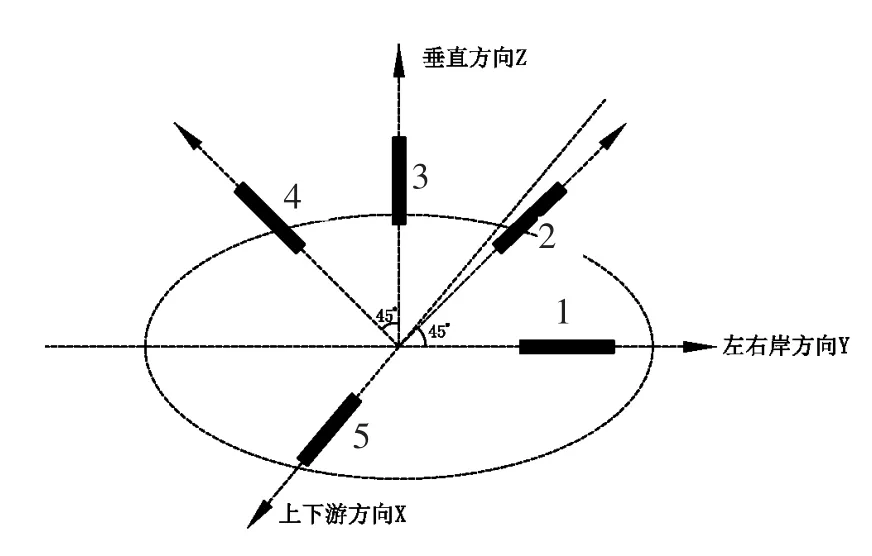
图2 五向应变计组示意图Fig.2 Sketch drawing of the directions of the 5-d stain meters

根据弹性变形理论，在坝体内的任意一点，三个互相垂直方向应变ε1、ε2、ε3之和为一个常数。在理想情况下，图2所示的五向应变计组中有：ε1+ε3+ε5=ε2+ε4+ε5，即ε1+ε3=ε2+ε4。

实际上总存在观测误差，而且应变计组的各支应变计并不是在一个几何点上，因而上式并不相等，须进行应变平衡。平衡后的单轴应变计算公式如下：

2 坝体应力

2.1 应力计算

由计算所得的单轴应变，结合混凝土徐变试验资料及弹性模量试验资料，利用变形法计算混凝土应力。

变形法将单轴应变过程线划分成若干时段，根据徐变的概念，每一时段的应力增量都将引起该时段的瞬时弹性变形和徐变变形，二者之和为总变形，对以后各时段的应变都将产生影响，计算各个时段应力增量时都应加以考虑。变形法的基本计算公式如下：

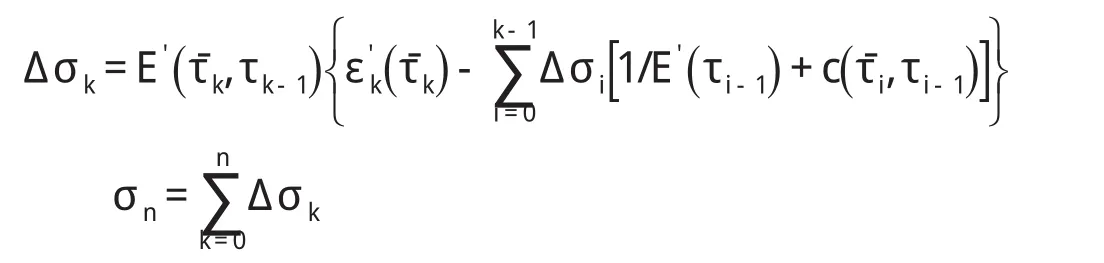
式中：Δσk——τˉk时刻的应力增量；

Δσi—— τi-1～ τi时段的应力增量；

σn——τˉk时刻的实际应力；

利用本实验室变形法应力计算程序对资料进行处理，表3为变形法计算所得8号坝段应力成果，“+”表示受拉，“-”表示受压。由于2009年至今施工未完成，水库尚未蓄水，成果只反映施工期应力情况。

2.2 坝体应力应变分析

2.2.1 自生体积变形过程分析

自生体积变形主要是水泥在水化过程中由于化学作用而产生的变形，随着水化过程的结束而逐渐趋向结束。该坝在坝体内4个高程，即473 m、506 m、530 m、560 m处布设了无应力计。一般自生体积变形，无论是收缩或膨胀，基本上应是单调变化，尤其不应在水化过程基本结束后还发生周期性变化。从推求得的混凝土自生体积变形看，大部分测点为单调膨胀变形，但有些测点出现了先收缩后膨胀的不单调发展情况，笔者认为这是由于外界温度的影响，造成无应力测值包含温度应力部分，已不完全是无应力状态，这对后面的应力计算精度有影响。

2.2.2 应力过程分析

从单个测点应力统计情况看，最大拉应力一般在1 MPa以下，个别测点最大拉应力超过1 MPa，实测最大拉应力为1.57 MPa，为S1测点，发生在相应部位混凝土浇筑后约8个月。根据该电站混凝土配合比及性能试验成果报告，此时混凝土抗拉强度大于2 MPa，故该点处拉应力处于允许范围内。从

坝体整体应力变化过程看，目前坝体混凝土拉、压应力皆在允许范围内变化。

（1）垂直方向（z向）应力分析

坝体混凝土垂直方向应力基本表现为压应力。在应变计埋设初期，一些测点出现拉应力，随着坝体混凝土浇筑升高，z向混凝土压力保持缓慢增加。目前压力数值稳定，压应力水平在0.44～1.52 MPa之间，整体表现为受压状态，坝踵不存在被拉裂的危险。

（2）上下游方向（x向）应力分析

上下游方向应力多数表现为拉应力状态，少数测点为压应力状态。目前应力数值在-0.29～0.78 MPa之间，在混凝土抗拉、抗压允许范围内变化。

（3）左右岸方向（y向）应力分析

左右岸方向应力多数表现为压应力。少数测点为拉应力，但随着时间推移，应力数值缓慢向压应力发展。目前左右岸方向应力数值在-1.1～0.29 MPa之间，混凝土应力数值和分布均在合理的范围内。

3 结语

（1）采用变形法计算了该坝8号坝段的混凝土应力，分析了该坝段的混凝土应力状态，对该坝段的应力状态做出了评价。分析表明，该坝段的应力数值在合理范围内变化，应力已趋于稳定，无明显的异常突变，可认为该坝段的应力状况良好。

（2）用变形法计算应力存在一个精度问题，原因在于变形法计算时把应力变化过程当成是台阶式的变化，但实际应力变化过程是连续过程。大量的监测资料表明，利用应变计组计算的混凝土应力准确性有限。要进一步提高应力计算的准确性，除严格按照规范进行仪器埋设、定时采集数据外，还应重点创新新的应力计算方法。

[1]储海宁.混凝土坝内部观测技术[M].北京:水利电力出版社,1989.

[2]李珍照.大坝安全监测[M].北京:中国电力出版社,1997.

[3]刘宇利,黄立波,杨威.江垭大坝应力应变监测资料分析[J].大坝与安全,2011(04).

[4]王同生.混凝土自生体积变形与无应力计[J].水利规划与设计,2009(5).