固态断路器中快恢复二极管的反向恢复模型

彭振东 任志刚 王华敏

（中国船舶重工集团公司第七一二研究所舰船综合电力技术国防科技重点实验室，武汉 430064）

0 引言

基于功率半导体器件的固态断路器，因其分断时不产生电弧，能快速完成电路分断，具有广阔的应用前景。快恢复二极管作为一种重要的半导体开关器件，在固态断路器中得到了广泛的应用。但是二极管关断时的反向恢复过程会影响断路器的安全工作和运行性能，因此需要建立能准确描述快恢复二极管反向恢复过程的模型，指导断路器参数设计，优化断路器性能[1-2]。

二极管模型主要分为功能模型和物理模型两大类[3]。功能模型只考虑器件的外部特性，不考虑器件内部复杂的物理过程，仿真速度快，但是精度不够。物理模型虽然精度很高，然而需要的参数太多，并且计算速度很慢。Lauritzen利用“分段”概念，将传统的物理模型进行简化，仅含两个参数，可方便的从数据手册中提取出来[4]。

Matlab因其强大的控制系统优化设计功能而在电力电子电路仿真中获得广泛应用，本文在Simulink中实现二极管的反向恢复模型，让其功率器件模型更完善，仿真更精确。

1 二极管的反向恢复模型

在常规的功率二极管基础上通过少子寿命控制技术来获得快恢复二极管，图 1所示为典型p-i-n二极管通态时的载流子分布情况[5]。

1.1 二极管关断过程

由图2（a）测试电路得到二极管关断感性负载时的电流波形如图 2（b）所示[6]。t＜0时，S1断开，S2闭合，二极管稳态导通；t=0时，S1闭合，S2断开，二极管电流开始以diF/dt=－VR/L的速率减小，进入关断过程的载流子清除阶段，直到正向电流减小到零并反向增加至反向恢复电流峰值 Irrm时，才基本完成对 i区过剩载流子的清除工作；此后（t＞T1），少数载流子已不充分，二极管开始恢复阻断功能，其反向电流开始迅速减小到反向饱和电流值。

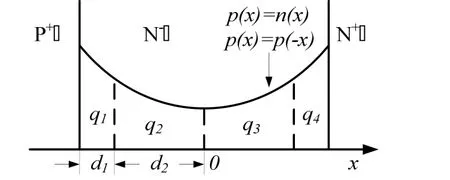
图1 二极管通态载流子分布

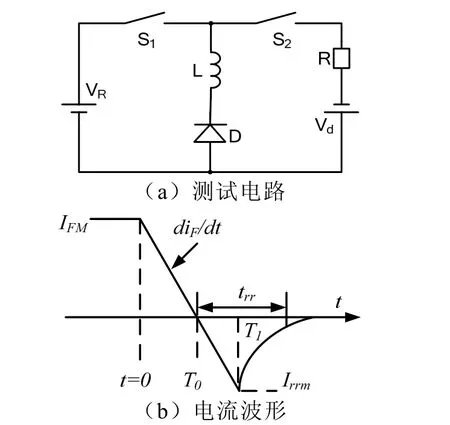
图2 二极管关断感性负载时电流波形

1.2 集总电荷模型

集总电荷的概念是将电荷存储区分为几个部分，过量的存储电荷被集中置于每个存储部分中间的一个节点中。在大注入条件下，中性区电子与空穴浓度相等，即p(x)=n(x)。当二极管正向导通时，假定电荷 q1、q2、q3、q4储存在图 1所示的四个节点当中。为了使模型简化并且能符合实际运行情况，我们认为电子与空穴在 i区对称分布，且d1＜＜d2。在模型中我们让d1→0，那么在忽略x=－( d1+ d2)处电子电流的条件下，根据载流子运动方程可得二极管电流为[4-5]

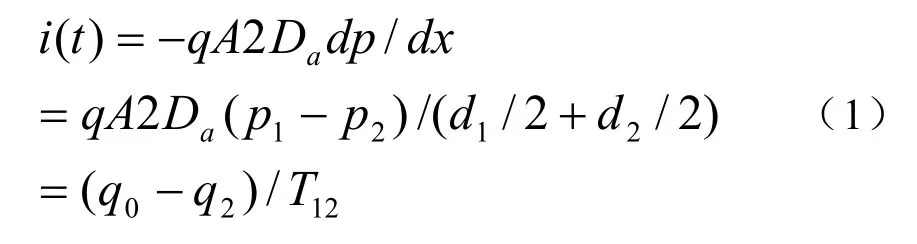
式中，q为电荷电量，A为 pn结横截面积，Da为双极扩散系数，p1为 d1区的平均空穴浓度, p2为 d2区的平均空穴浓度，q0＝qAd2(p1-pi0)表示d1→0 时 d1区的剩余电荷，q2＝Ad2(p2-pi0)表示d2区的存储电荷，T12=d22/4Da表示穿过d2区的运输时间。

设载流子寿命为τ，电荷连续方程为

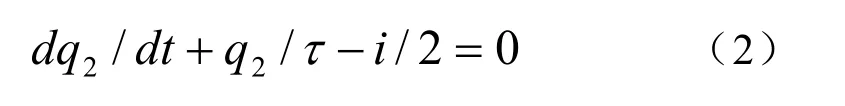
令 qM＝2q2，TM＝2T12，qE＝2q0，则完整的二极管模型如下

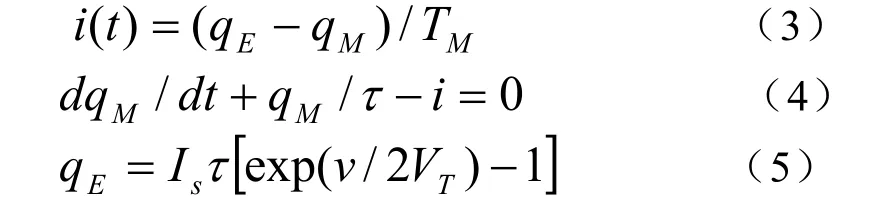
式（5）中Is为二极管反向饱和电流，v为二极管结电压，VT=kT/q为温度电压当量，k为玻尔兹曼常数，T为pn结绝对温度。

1.3 模型参数提取

图2（b）中的反向恢复时间trr，反向电流峰值 Irrm及测试条件 diF/dt，IFM均能从产品手册中获得。设α=－diF/dt，τ为i区少子寿命，则在少数载流子清除阶段（0≤t＜T1），由 i(t)=IFM－ɑt可得

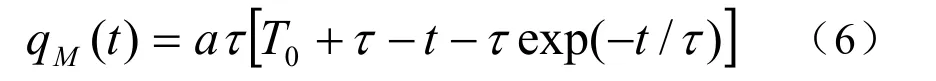
当t=T1时， qE=0，则

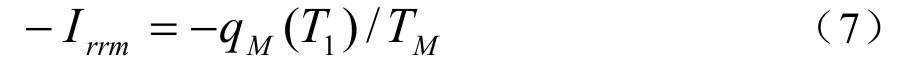
当t≥T1，二极管开始恢复阻断功能，反向恢复电流开始独立于反向电压，由式（3）、（4）、（7）和qE=0联立得

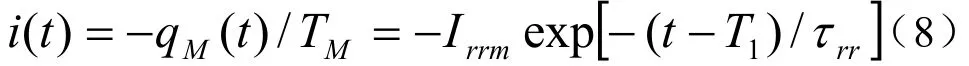
其中τrr为反向恢复时间常数，满足如下关系

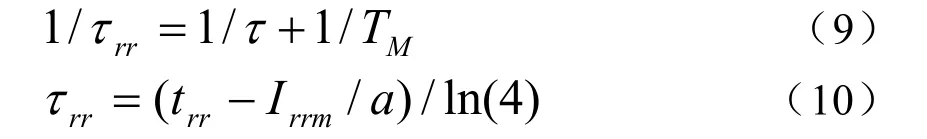
联立式（6）和（8）并令t=T1，则

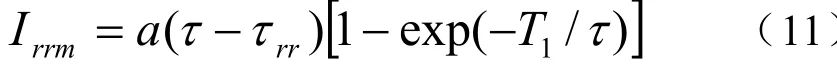
先从式（10）计算τrr，再利用式（11）求得τ，然后从式（9)中解得参数TM。

2 模型的实现

本文利用 MatlabSimulink中的模块对上述模型进行实现。模型以可控电流源为核心部件，通过电压传感器采集电流源两端的实时电压并传给控制子系统，控制子系统接收模型参数和实时电压值，按照式（3）、（4）和（5）进行计算，得到二极管的实时电流值，将该电流值作为可控电流源的控制输入信号。如图 3所示，其中的 IC模块是为解决仿真出现代数环而加入的。

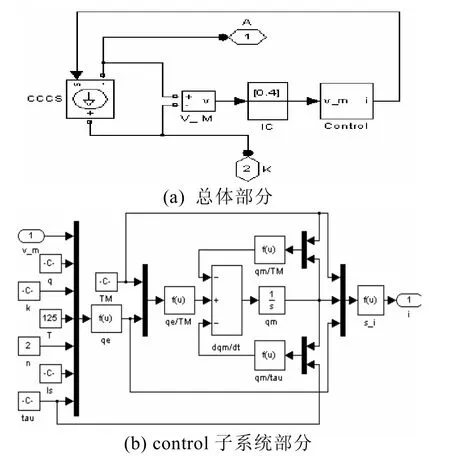
图3 二极管模型的Matlab实现

3 仿真和实测结果

本文对 ABB公司的快恢复二极管5SDF04D4504进行了建模和仿真，模型主要参数见表 1，按数据手册标准测试条件进行了测试，结果见表2和图4。

表1 模型主要参数

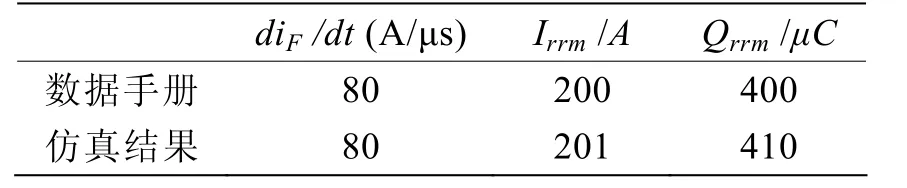
表2 反向恢复主要参数

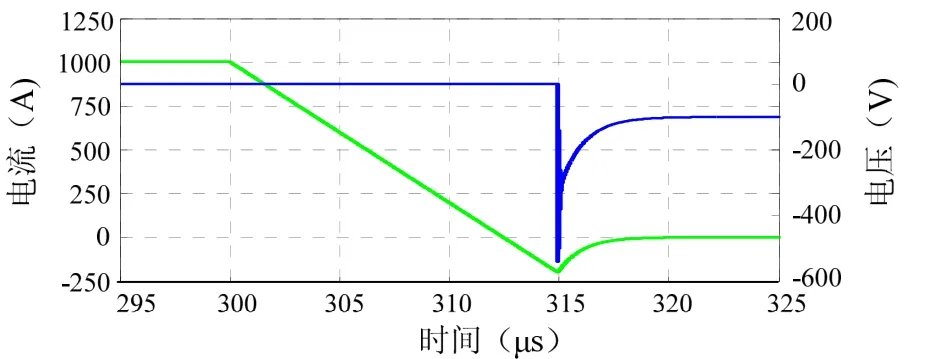
图4 关断电压电流仿真波形

不同 IFM条件下，Irrm随－diF/dt变化的仿真结果如图5所示。

从上述仿真结果可以看出，在标准测试条件下，二极管反向恢复特性主要参数与数据手册中保持一致，仿真波形和数据手册实测波形比较吻合，表明所建模型的有效性，能在一定工作条件下对快恢复二极管的反向恢复特性进行准确的模拟。但是在图5中，当IFM和－diF/dt较小时，Irrm的仿真结果比数据手册中的值小；当 IFM和－diF/dt 较大时，Irrm的仿真结果比数据手册中的值大。这是因为模型的参数是根据IFM=1000 A，－diF/dt=80A/μs来提取的，不同条件下的Auger复合效应的不同以及式（1）中忽略电子电流所造成的误差均会影响仿真结果的精度。除此之外，trr的差异和实际二极管的电容效应也会给仿真结果带来偏差。

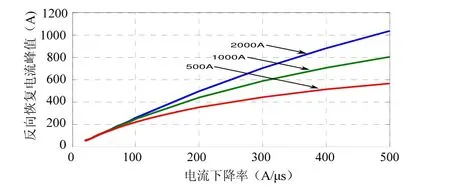
图5 Irrm随IFM和－diF/dt的变化曲线

4 结论

本文分析了固态断路器中快恢复二极管的反向恢复特性，并在MatlabSimulink中建立了反向恢复的集总电荷模型。仿真结果与数据手册对比结果表明了该模型的有效性，在一定范围内能对快恢复二极管的反向恢复特性进行准确的模拟，具有一定的实用性，可用于固态断路器和其他大功率变换器的仿真当中。

[1]温家良, 傅鹏, 刘正之, 汤广福.EAST托卡马克大功率双向直流快速晶闸管开关可靠关断理论分析及参数优化设计[J]. 中国电机工程学报, 2005, 25（14）：62-67.

[2]易荣, 赵争鸣, 袁立强.高压大容量变换器中快恢复二极管的模型[J].电工技术学报,2008, 23（7）： 62-67.

[3]Kraus R, Mattausch H J. Status and trends of power semiconductor device models for circuit simulation[J].IEEE Trans. on P. E. , 1998, 13： 452—46.

[4]Ma C L, Lauritizen P O. A simple power diode model with forward and reverse recovery[J]. IEEE Trans. On Power Electron. , 1993, 8(4)： 342—346.

[5]维捷斯拉夫·.本达. 功率半导体器件—理论及应用[M].北京： 化学工业出版社, 2004.

[6]汤广福, 刘文华.提高电网可靠性的大功率电力电子技术基础理论[M].北京： 清华大学出版社, 2010.