基于Saber的高压大功率IGCT器件的建模与仿真研究

张新民 李明勇 代科

(中国船舶重工集团公司第七一二研究所，武汉 430064)

0 引言

由瑞士ABB公司研发的大功率IGCT器件，以其低感的门极驱动电路，优化的可控硅技术，高度集成化，应用简易化等优点，成为中压传动领域，机车牵引，工业，输配电行业的半导体器件的可靠选择[1]。近年来，围绕着 IGCT功率器件的建模，成为IGCT应用中的一个研究热点。然而，在当前的仿真工具，如MATLAB，Pspice，Saber等软件中，都没有现成的IGCT功率器件模型，给IGCT功率器件的应用带来诸多不便。

从已有的文献来看，IGCT建模的方法有：基于载流子运动的物理模型，电荷控制模型，电学模型，以及功能模型。物理模型[2,3]，以载流子的运动过程建模，最贴近功率器件的实际开关过程，仿真精度高，但参数过多，不易获取。电荷控制模型[4]以双晶体管作为 IGCT等效模型，过程繁杂。功能模型[5]以符合实际器件开通关断波形特点为前提，建模过程相对简单，且具备一定的仿真精度，特别适合于实际工程应用。在当前仿真环境中，Saber仿真软件与Pspice及MATLAB相比，在电力电子暂态仿真中，具有明显的优势。本文采用 Saber仿真软件，建立 IGCT的功能模型，并应用于仿真电路中，以期达到实际工程应用的目的。

1 IGCT开通关断暂态分析

IGCT开通关断的一般波形可从IGCT器件的datasheet参数表获得。

从图 1可以看出，IGCT开通和关断过程都是在开通关断信号发出后经过一定的开通关断延时开始的，对IGCT而言，开通关断延时时间约为几个微秒。开通时，IGCT电压近似直线下降，电流线性上升，经过一个波峰后，下降到通态电流水平。电流峰值由与之相连的IGCT反并联二极管反向恢复电流引起。关断时，电流的下降分为两个过程，tf时段内电流下降阶段及拖尾电流阶段，两阶段电流近似线性下降；关断过程中电压出现两个波峰，VDSP与功率回路中串联杂散电感有关，其值随着杂散电感的增大而增大，关断过程的第二个尖峰VDM与DC-Link环节参数相关，主要随着RS、LS1、LS2的增大而增大，随着箝位电容 CCL的增大而减小。因而，可将IGCT在开通过程中等效为可变电压源，其特性可用一阶线性电路来模拟；在关断过程中等效为可变电流源，其特性可用分段二阶电路来模拟，第一阶段持续的时间由下降时间tf确定，第二阶段持续的时间由拖尾电流时间确定，通常为20～30 µs左右。

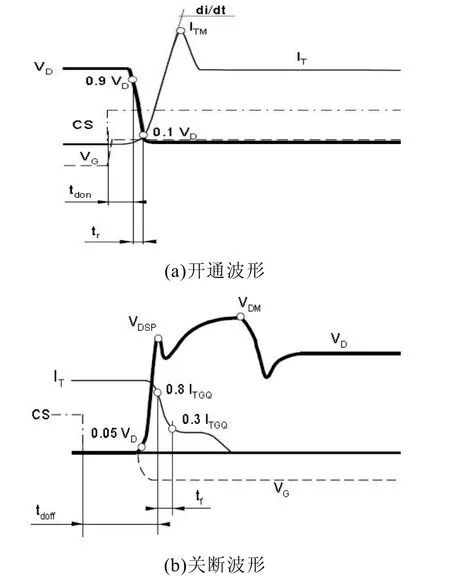
图1 IGCT开通关断的一般波形

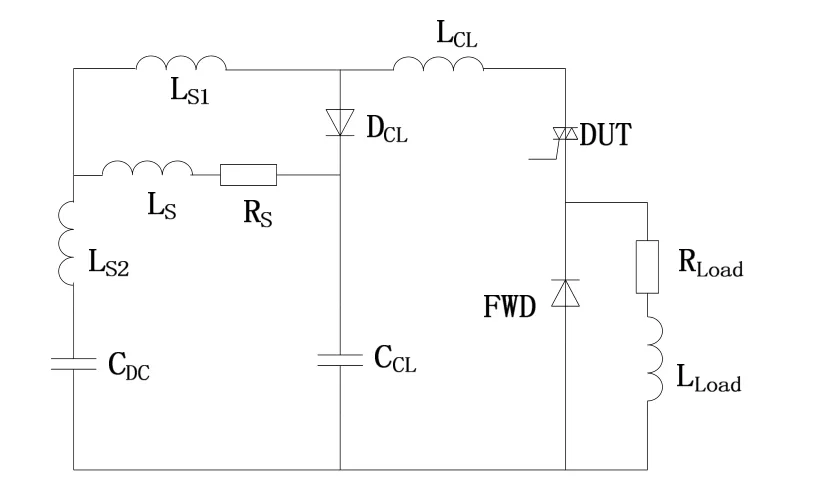
图2 IGCT测试电路

2 Saber中仿真模型的建立

2.1 开通过程等效电压源模拟

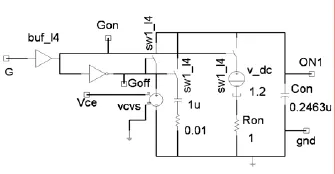
图3 开通过程模拟

开通过程将 IGCT看成一可变电压源，电压近似线性下降，用一阶 RC电路来模拟。如图 3所示，Gon及Goff分别为门极信号经过延迟后的开通和关断信号；电容 Con的初值为 IGCT断态时加在器件两端的电压，通过VCVS-Con回路充电获得；电路中V_dc的值用来表示IGCT的通态压降，其值随器件功率等级而变。

开通过程的电压方程如式(1)。

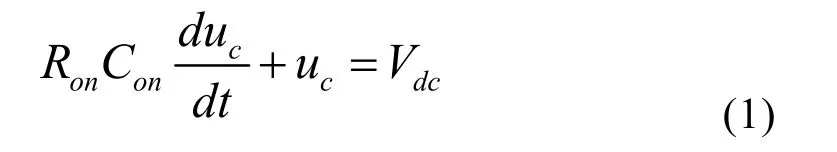
由式(1)得到

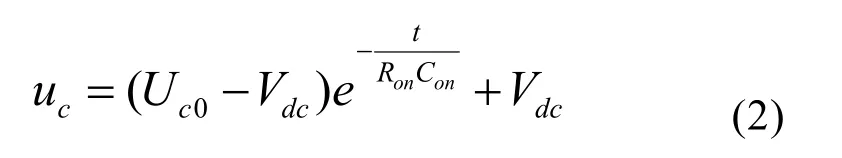
式(2)中，Uco为电容 Con的初值。通常经过 3～4个时间常数τ，电压uc稳定在Vdc。

2.2 关断过程等效电流源模拟

关断过程将 IGCT看作一可变电流源，用两个阶段的二阶RLC电路来模拟。通态时通过回路vcvs1-sw1-sw3-Cini-R2及回路 vcvs1-sw1-Coff2使电容Coff2及Cini初值为通态电流值ITo。关断过程的初始阶段，电容Coff2通过回路Coff2- sw2- vcvs2-Loff1-Roff1- pwld1放电，该阶段结束后，电容Coff2的值稳定在k1·ucoff2(k1为vcvs2的比例系数)；关断拖尾阶段电容 Coff2通过回路 Coff2-sw4-Loff2Roff2-pwld2放电，放电结束后，电容Coff2上的电压趋近于零。通过压控电流源Coff2上的电压变化特性即为IGCT关断过程的电流特性。

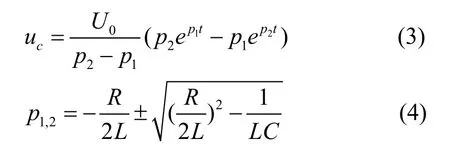
图4 关断过程模拟环节

2.3 仿真参数

选择 ABB公司型号为 5SHX19L6010型IGCT器件作仿真原型。各环节仿真参数如表 1所示。其中 tplh，tphl分别为开通，关断设置的延迟时间。

表1 模型仿真各器件参数

3 IGCT仿真及实验结果

仿真及实验主电路如图 5所示，应用 Saber层次图将IGCT封装为元件模型，方便仿真调用。如图所示，电路由4个IGCT组成两电平H桥，前端配置DC_Link环节。

采用的 IGCT的型号为 ABB的5SHX19L6010电路中的各参数如下，VDC=1500 V，Lcl=320 nH，Ls1=3.7 µH，Rs=1.25 Ω，CDC=5 µF，Cc1=2 µF，Rload=4Ω，Lload=2 mH 两电平 H桥的调制采用载波层叠法，调制原理如图6所示。其中调制波与正向载波 carrier_1比较用于控制IGCT4，IGCT1的控制信号为正R＞2半周导通负半周关断，IGCT3的控制信号与IGCT1相反，调制波与负向载波carrier_2比较作为IGCT2的脉冲信号。

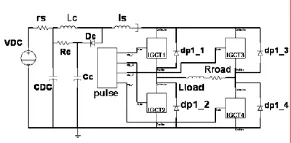
图5 IGCT两电平H桥原理图

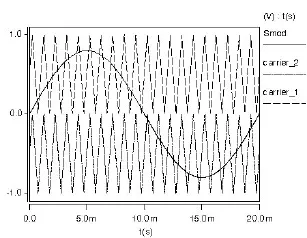
图6 载波层叠调制原理图

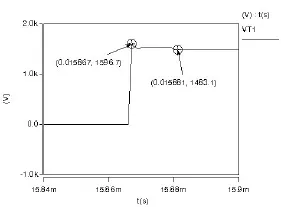
图7 仿真关断波形

图7、图8给出了IGCT1的关断波形，IGCT2的开通波形，图9示波器的第一个波形为IGCT1关断波形，仿真波形与实验波形保持着良好的相似性，体现在关断过程的第一波峰及第二波峰的幅值大致相当，另一波形为IGCT2的开通波形，开通时间与实验波形较一致。

图10为电路运行过程瞬态波形，从上至下四个波形依次为 IGCT1，限流电感 Lc，IGCT3，IGCT4两端上的电压波形。在这个瞬间，VT3常通，VT2斩波，VT2关断瞬间，由VT1反并联续流二极管续流，续流过程中，负载输出电压逐渐降至零，限流电感电压逐渐上升至母线电压，VT3，VT4上的电压被箝位为零。

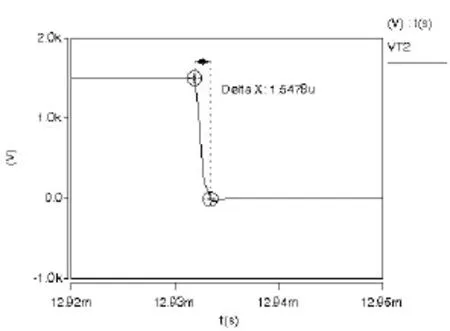
图8 IGCT开通波形

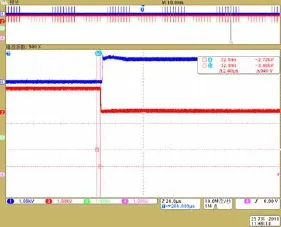
图9 开通关断实验波形

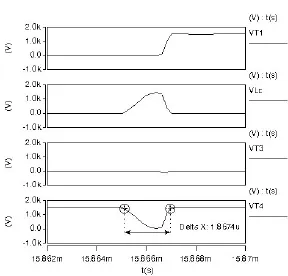
图10 瞬态波形

图11实验瞬态波形与仿真波形一致，持续时间大致相当。从仿真与实验对比的结果看，验证了本文在 Saber中所建立的 IGCT功能模型的准确性及实用性。

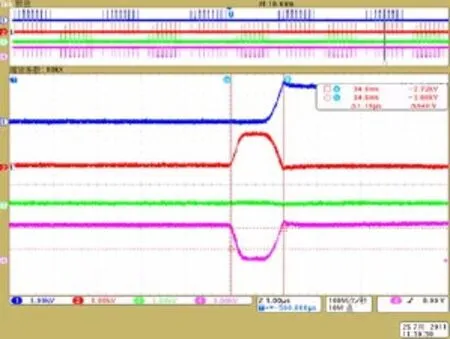
图11 瞬态实验波形

4 结语

本文在 Saber中建立了 IGCT的功能模型。在该模型中，IGCT开通及关断时分别等效为可变电压源及可变电流源。通过软件仿真以及与实际波形的比较分析，结果表明了该功能模型的有效性，可作为IGCT选型及电路设计的参考依据。

[1]Nagel, S. Bernet, P. K. Steimer,etc. A 24 MVA Inverter using IGCT series connection for medium voltage applications[J]. Thirty-Sixth IAS Annual Meeting.Conference Record of the 2001 IEEE,vol.2,867 ～870 .

[2]H. Kuhn and D. Schroder. A new validated physically based IGCT model for circuit simulation of snubberless and series operation[J]. Industry Applications Conference, 2000. vol.5, 2866 ～ 2872.

[3]H. Kuhn and D. Schroder. Implementation and validation of a physics-based circuit model for IGCT with full temperature dependencies[J]. Power Electronics Specialists Conference, 2004, vol 1, 597 ～603.

[4]张华曹, 段飞. IGCT综合型电荷控制模型的建立和仿真[J]. 电子器件, 2003, 26(1)： 25～28.

[5]袁立强, 赵争鸣, 白华等. 用于大功率变流器的IGCT功能型模型(英文)[J]. 中国电机工程学报,2004, 24(6)： 65～69.

[6]邱光源. 电路. 北京： 高等教育出版社, 1999.