基于PMU的支路电压稳定指标研究
张洪喜
(南瑞继保电气有限公司,江苏 南京 211106)
随着负荷的增加、输电线路传输功率的不断增长,电压稳定问题日益突出。电力系统实时电压稳定预警与控制是防御电力事故的重要环节。开发实用性高的电压稳定指标是目前广域电压保护课题的研究重点[1]。随着PMU测量技术的发展,国内外许多学者提出了基于PMU的电压稳定指标[2]。这些指标以负荷端母线电压为研究对象,反映支路运行状态的电压稳定指标研究较少[3]。在实际的电力系统中,不同区域之间的功率传输能力是影响电压稳定的重要因素[4]。开发普适的支路电压稳定指标是十分必要的。
本文提出基于PMU测量量的支路电压稳定指标LVSIK。该指标利用PMU测得的同步数据、综合考虑支路传输有功和无功两方面的因素,不受功率因数变化的限制,有很强的普适性。
1 支路电压稳定指标模型
对于系统中任一支路,利用PMU测量量对其网络等值[5]。原始网络如图1所示。
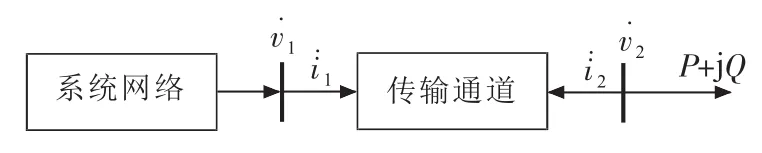
图1 原始网络图
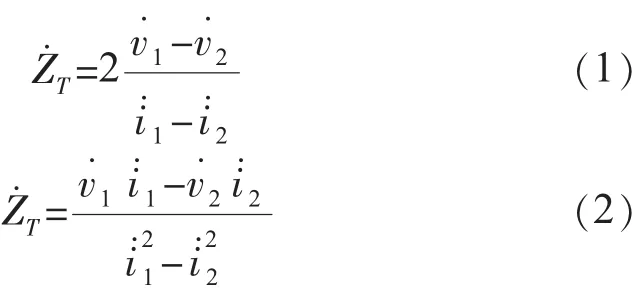
利用式(1)和式(2)将传输通道进行T型等值。等值后的模型如图2所示。
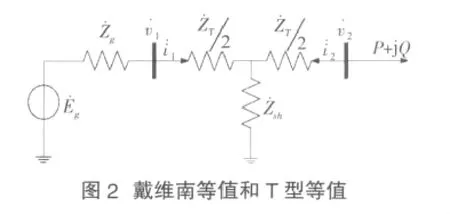
将模型进一步等值为简单两节点系统:

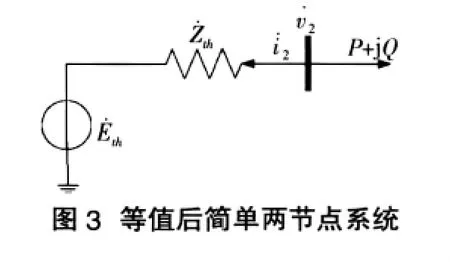
2 支路电压稳定指标定义
[5]中提出的支路电压稳定指标是将支路传输的功率等值为恒定阻抗ZL,用支路等值阻抗Zth和负荷ZL的比值来确定支路有功传输极限[5]。当Zth/ZL=1时,节点电压达到临界值,但是功率不一定达到极限值。只有在功率因数恒定的情况下,支路传输的有功才达到极限值Pmax,指标定义为:
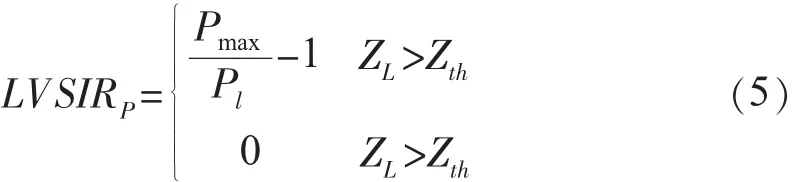
该指标从支路有功传输量来定义支路电压稳定指标,只适用于功率因数恒定的情况。支路功率传输能力的大小反映了系统电压的运行情况。随着负荷功率的增加,支路传输的功率逐渐增加,节点电压逐步下降。当电压下降到临界点时,支路传输的功率达到极限[7]。根据图3所示等值两节点系统,由支路潮流计算方法得:
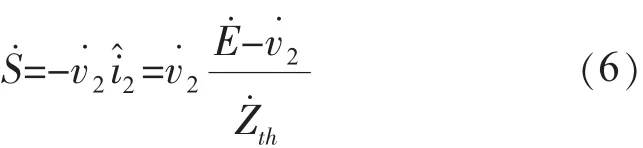
将式(6)的实部与虚部展开后得:
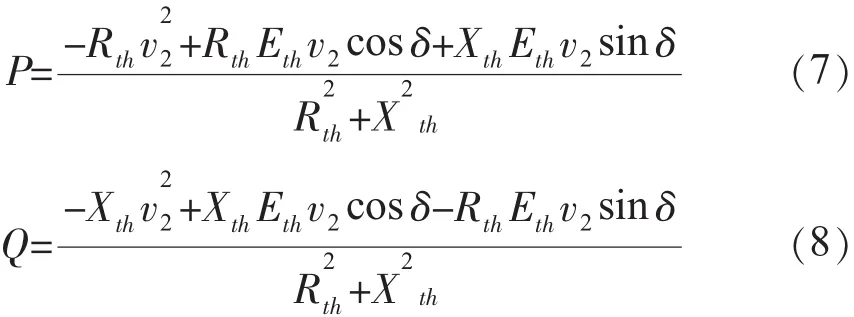
式(7,8)中:δ=δ1-δ2。
式(7)是P关于电压的一元二次函数,式(8)是Q关于电压的一元二次函数。它们的二次项系数都为负值,存在最大值点。根据式(7)和式(8),当dP/dv2=0时P达到最大值;当dQ/dv2=0时Q达到最大值[8]。它们达到最大值时的电压计算公式为:
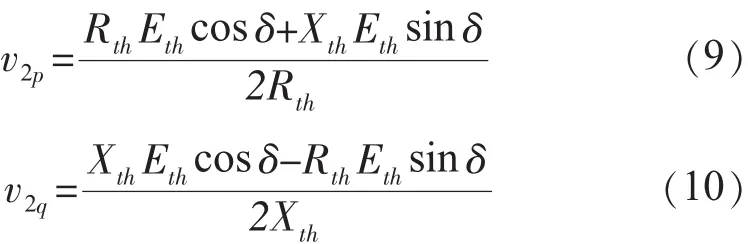
分别将式(9)和式(10)带入式(7)和式(8)可得P与Q的传输极限:
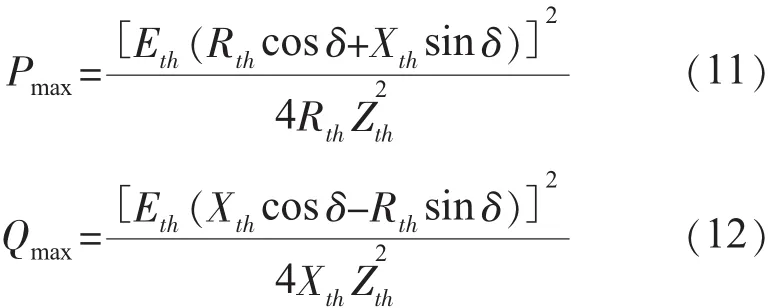
根据式(11)和式(12),定义支路的有功电压与无功电压稳定指标为:
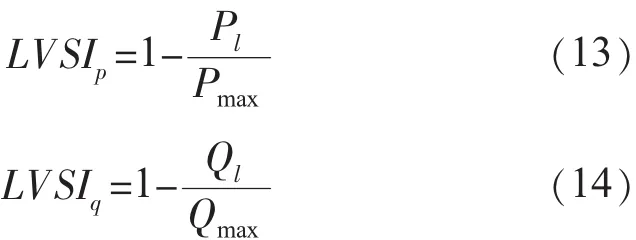
式(13,14)中:Pl和 Ql为支路当前有功与无功传输量。这两个指标反映的是同一支路在同一时刻的有功与无功传输能力的大小。在网络正常运行情况下,它们的取值区间为(0,1),其中0为临界点。综合考虑有功和无功这两方面的影响因素[9],定义某支路i在时刻k时的支路电压稳定指标为:
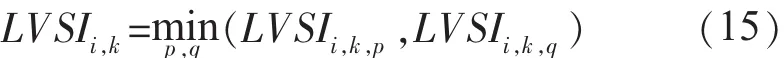
式(15)反映的是支路中功率传输能力的大小,它的值反映了支路的运行状态。该指标值越小,支路的功率传输能力就越小。当负荷端功率逐步增加到临界点时,支路的传输能力将达到极限,受端电压将达到临界点。如果进一步增加负荷端功率,支路将无法传输更多的功率,受端电压将会崩溃,进而扩展到整个网络[10]。对整个网络中所有或部分关键支路和传输通道的功率传输能力进行实时监测,定义整个网络的支路电压稳定指标为:
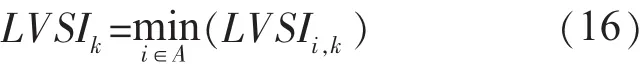
式(16)中:A为网络中需要监测支路或通道的集合。网络的电压崩溃最先发生在指标LVSIk的值最小的位置[11]。
3 算例分析
算例以IEEE14节点系统为研究对象。在变功率因数的情况下,分别增加第14号负荷节点的有功和无功,使14号节点电压逐步下降到临界点处。同时监测与14号节点强相关的四条支路传输的功率相量及这些支路两端的电压、电流相量。用这些仿真量模拟PMU的实测数据进行仿真分析。
将14号节点PV曲线的上半支和L13-14的支路电压稳定指标进行比较的仿真曲线如图4所示。
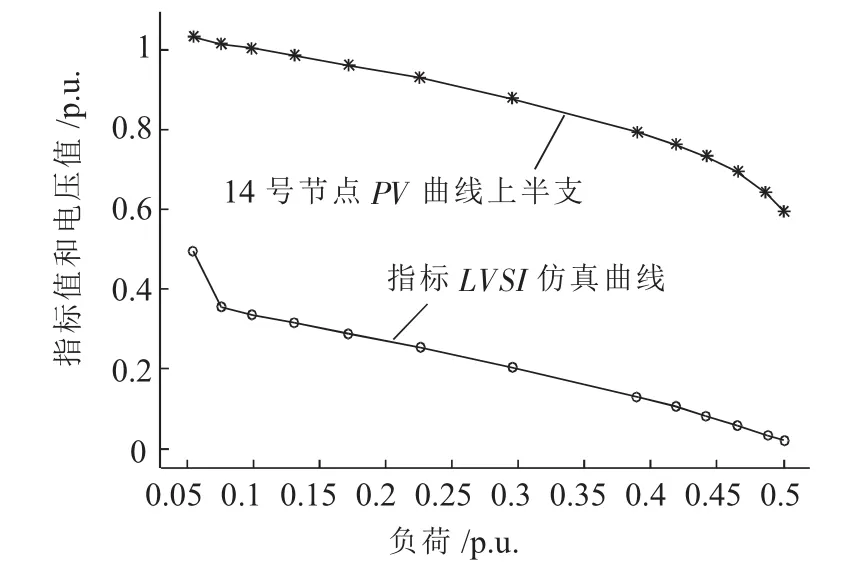
图4 L13-14指标曲线与PV曲线比较
从图4可以看出,随着14号节点负荷功率的增加,节点电压在下降,支路电压稳定指标值在减小。当电压逐渐降低到临界点时,支路电压稳定指标值随之降低到0附近。节点电压的临界点与支路指标的临界点功率都在0.5附近,因此支路指标值能够反映支路的运行状态和受端电压的稳定情况。
支路指标LVSI、参考文献[5]中支路指标LVSIR和14号节点PV曲线的上半支进行比较的仿真曲线如图5所示。
从图5中可以看出,支路指标LVSI随着负荷的增加逐步减小,在功率临界点处减小到0附近。而参考文献[5]中的支路指标LVSIR的值也随负荷的增加而降低,但是它在功率临界点之前达到0。这说明在功率因数变化的情况下,指标LVSIR存在一定的误差。

图5 L13-14的LVSI指标与LVSIR指标比较
与14号节点强相关的4条支路电压稳定指标LVSI和14号节点PV曲线上半支的仿真曲线的比较如图6所示。
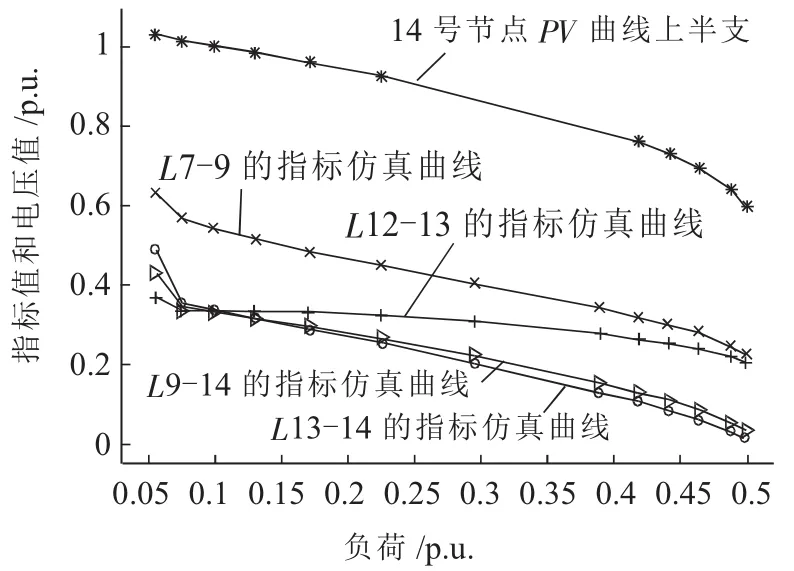
图6 4条支路的LVSI指标曲线的比较
在图6中,随着负荷节点功率的增加,4条支路指标值逐步减小,说明这些支路的功率传输能力在下降。在负荷功率增加过程中,支路L13-14和支路L9-14的指标值小于支路L7-9和L12-13的值。且在电压临界点处,支路L9-14和L13-14的指标值接近于临界值0,而支路L7-9和L12-13的值在0.2附近。这是因为支路L9-14和L13-14与14号节点直接相连,14号节点负荷功率的变化直接影响这两条支路的运行状态。临界点处4条支路电压稳定指标LVSI的值从小到大排列如表1所示。
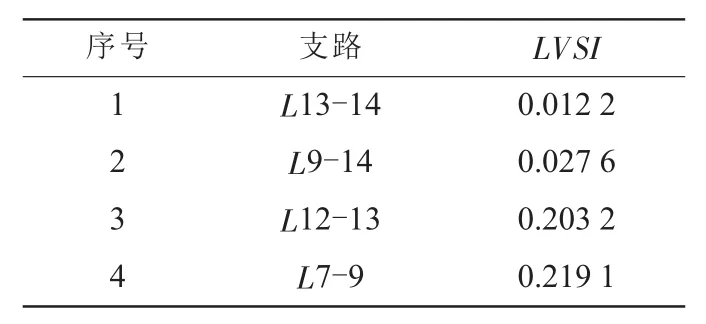
表1 功率临界点处LVSI值排序
从表1可以看出,在电压临界点处,支路L13-14和L9-14的指标值都很小,接近于0,它们是系统中的弱传输支路。因此通过支路指标的仿真分析可以确定网络中每条支路的运行情况,找出网络中的薄弱支路,增强了电力调度中心对电力系统的动态稳定检测和分析能力,为调度人员及时采取预防控制措施提供可靠依据。
4 结束语
本文利用PMU测量量开发了支路电压稳定指标LVSI。用该指标值的大小来确定网络中支路的薄弱程度,进而分析网络的电压稳定情况。该指标综合考虑了有功和无功两方面的因素,且避免了负荷功率因数恒定的限制。用IEEE14节点系统对该指标进行了仿真分析。仿真结果表明该指标能正确反映支路的运行状态和系统电压稳定的实际情况。
参考文献:
[1]薛禹胜,徐 伟,DONG Zhaoyang,等.关于广域测量系统及广域控制保护系统的评述[J].电力系统自动化,2007,31(15):1-5.
[2]闫常友,刘建飞,杨奇逊.基于当地量的电压稳定指标[J].电力系统自动化,2006,30(5):29-32.
[3]邢卫荣.基于PMU分析的电力系统电压稳定指标研究[D].南京:东南大学电气工程学院,2008.
[4]刘道伟,谢小荣,穆 刚,等.基于同步相量测量的电力系统在线电压稳定指标[J].中国电机工程学报,2005,25(1):13-17.
[5]REHTANZ C.Wide Area Monitoring and Control for Transmission Capability Enhancement[R].GIGRE,Paris,France,2006.
[6]牟善科,丁 涛,顾 伟,等.基于偏差校正的戴维南等值参数在线跟踪改进算法[J].电力系统保护与控制,2011(2):23-28.
[7]周双喜,朱凌志,郭锡欢,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2004.
[8]MILOSEVIC B,BEGOVIC M M.Voltage-stability Protection and Control Using a Wide-area Network of Phasor Measurements[J].IEEE Transactions on Power Systems,2003,18(1):121-127.
[9]常森伟,安天瑜,周苏荃.基于支路潮流的电压稳定指标研究[J].黑龙江电力,2007,29(4):252-254.
[10]姜 彤,艾 琳,杨以涵.基于支路裕度的在线电压稳定指标[J].电力自动化设备,2009,29(10):39-42.
[11]李大虎,曹一家.基于同步相量测量的实时电压稳定分析方法[J].电力系统自动化,2006,30(12):17-22.
[12]顾 伟,万秋兰.广域电压检测的线性稳定指标研究[J].电工技术学报,2010,25(1):1-6.

