白山地区地球化学元素组合分布特征及其地质意义

毕明丽

（长春工程学院勘查与测绘工程学院，长春130021）

0 引言

随着勘查地球化学的深入发展，对区域分散流和次生晕异常，即区域地球化学异常的评价日益引起人们的重视［1］，如何有效地评价地球化学异常成为众多勘查地球化学家关注的焦点［2］。由于地球化学元素直接携带某种矿化信息，对地球化学元素的空间关系进行精细化分析可以直接或间接地揭示矿化溯源问题。元素的富集规律和空间分布具有多重分形特征，地球化学元素分布规律的研究是揭示元素矿化富集及空间变化规律的重要途径之一［3－4］。传统意义上的化探异常处理方法一般均从单一元素入手，以单一元素的含量值与背景值之差来确定化探异常。这种方法简单、直观、适用，但单一元素异常分析往往凭高就位，单元素的含量值高低仅是求异的因素之一，而非唯一因素。事实上，某点元素含量高值也可能是环境污染所致，并不反映矿异常。

1 元素空间定量组合求异模型

成矿过程具有多期性和多源性，那么成矿条件也应是多样的。众多复杂地质因素对地球化学元素的控制必然表现出元素的群体特征，即共生组合特征。不仅原生晕元素具有共生组合特征，次生晕及水系沉积物分散流同样具有共生组合特征，只是一般情况下两者不呈一一对应关系。在元素共生组合中，各元素质与量的分配同样是不均衡的，即地球化学元素在空间组配上具有差异性，这种差异性有时表现为地质历史的阶段性差异，有时表现为空间组合关系上的差异性。

基于上述观点，本次采用因子—泛克里格模型对测区化探数据进行空间定量组合求异。因子分析方法具有压缩变量空间，再现原始变量内部相关关系的功能，利用因子取自原始变量线性组合及旋转变换这一处理技巧，可将化探数据矩阵中多元素变量集综合成少数具有特定含矿指示意义的元素定量组合指标，利用这些指标重新构造空间数据矩阵，作为求异基础，这些新的数据是统计量，仍具有空间结构性和相关性，在非平稳假设下，应用泛克立格法可求出漂移与剩余，从而确定异常。

在建模过程中综合借鉴因子分析与泛克里格法的原理，构造主因素泛克里格模型如下：

式中：n—— 样品数；

m——为地球化学元素变量数。

按因子分析原始模型

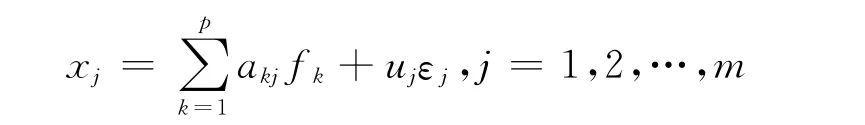
进一步求其旋转变换解（方差极大旋转或四次幂极小旋转）：

令F ＝ （f1，f2，…，fp）

则F＝XR－1B（R－1为X之相关阵逆阵）

即F ＝ （fkj）n×p，F 为因子计量阵。

然后对原始网格数据X重新构造，目的在于对变量进行线性组合，即构造所谓主成分，有：

因为PBL教学模式一般都是以小组的形式开展，所以，将学生进行合理地小组划分是最为关键的基础环节。小组划分应该以激发学生的参与积极性和主动性为基础，促使学生主动完成规定任务。教师则应对学生的英语口语水平进行综合评判，并根据水平差异进行小组划分，防止整体实力过强或者过弱。这样一来，才可以进一步避免在讨论的时候，出现强势或弱势极端群体。同时，教师还应在小组中，指定一名同学作为组长，负责小组成员的具体任务划分，并对小组成员的活动与讨论参与性进行实时监督。这就需要小组组长既具备良好的英语口语水平，又要具有一定的组织与管理能力。

将X（1）中的元素x（1）ik乘以相应因子计量，得：

其中，X（＊）中第j列可解释为以主因子fj为主的空间组合加权新变量，共P个。将X（＊）中元素每列按原始样品坐标顺序排列，构成P个点阵数据，每一点阵都相当于新的网格数据，于是可依空间分布的顺序进行求异。关于求异方法，将上述点阵数据理解成具有漂移的区域化变量Z（x），则

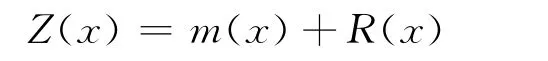
通过求数学期望m（x）可得R（x），即为区域异常。当然这里假定Z（x）存在变异函数，其增量具有一阶矩与二阶矩，在无偏性与最优性条件下通过解克里格方程组可求出m（x），这里的R（x）分布形态进一步可由DEM数字高程模型以图像形式表达出来。

2 白山地区地球化学组合分析

依原始数据矩阵X＝（xij）n×m进行原始数据的标准化处理，得到20个变量间的相关系数矩阵R（表1）。对其进行R型因子分析，只取大于1的特征值共有7个，其特征值分别为3.63、3.17、1.61、1.58、1.24、1.03、1.01，依次提取出7个互不相关的因子。这事实上得到了由7个公因子所确定的7维公因子空间。将20个变量简化成7个公因子，相当于将各变量用它们在公因子空间上的投影来代替，其方差贡献累计百分比达66%，可以认为这7个因子已包含原始变量大部分信息。

主因子解不是最终的因子解，基于因子解的不唯一性，以主因子解为基础寻求地质意义比较明显的而便于解释的因子解。主因子不满足：“简单结构准则”，出现相当多的中等载荷，使各因子的地质含义含混不清，不利于对因子进行解释。把载荷绝对值r＞0.5的元素看作该因子的主要载荷元素，求得各因子的特征组合（表2）。

根据方差极大正交旋转结合本区的地质概况，按因子载荷的大小将各因子所涉及的关联顺序排列（各关联中的正负号相当于正交因子轴的两端），可进行地质解释如下：

因子F1上具有高载荷的元素变量有：Co、Mn、Ti、Fe2O3。Fe、Co、Ti含量高，说明这部分元素基性程度偏高，属基性—超基性成因。且Fe、Co相关系数为0.6，Fe、Ti相关系数达0.8，元素间相关性较强。因子F1代表一个与Fe、Co矿化有关的基性元素的聚集过程。

因子F2上具有高载荷的元素变量有：Hg、Pb、Zn。Pb、Zn为亲铜族成矿元素，二者经常伴生，一起作为多金属矿的指示元素。Zn、Pb的相关系数达0.72。本组元素组合反映了低温热液成矿元素Zn、Pb为主的聚集矿化过程。

表1 相关系数矩阵

续表1

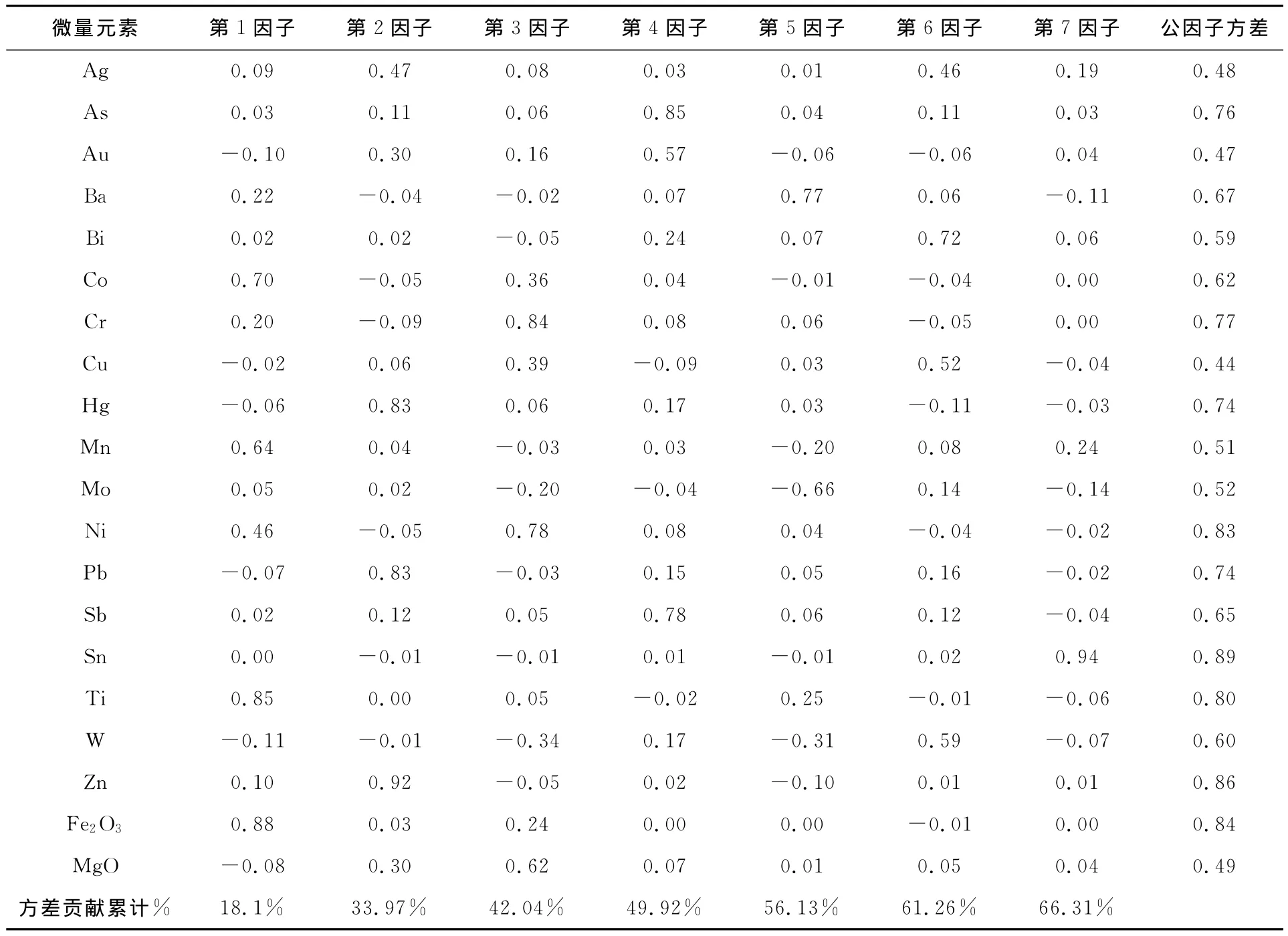
表2 方差极大正交旋转因子解

因子F3上具有高载荷的元素变量有：Cr、Ni、Mgo。Cr、Ni为亲铁族成矿元素，说明这部分元素与基性、超基性暗色火山岩类有关。且Cr、Ni相关系数达0.81，元素间相关性较强。

因子F4上具有高载荷的元素变量有：As、Au、Sb。砷、锑均为亲铜族成矿元素，属于岩石圈上部的稀有组分，地球化学性质接近，在自然界中常以自然砷、自然锑及砷锑合金的形式分布。这组元素的共生组合反映了中低温热液成矿元素的聚集过程，出现As、Sb矿化。

因子F6上具有高载荷的元素变量有：Bi、Cu、W。Bi、Cu二者为亲硫成矿元素。本组元素组合反映了与中酸性岩体有关的中高温热液成矿元素Cu、W的聚集矿化过程。

其他因子F5、F7上具有高载荷的元素变量少，且变量载荷也都很小，其地质意义较小。

3 组合异常空间分布DEM模型

数字高程模型（DEM）［5－7］原型是地形等值线的三维计算，地球化学元素组合及异常仍可用DEM进行三维表达。将墨江数据的公因子与泛克里格构和的元素组合水系沉积物地球化学异常计算结果分别以等值线。图［8］和DEM 表达（图1－5），从图中可观察异常的空间走向、规模与形态和空间分布位置。

图1 F1空间定量组合异常3D分布图

图2 F2空间定量组合异常3D分布图

图3 F3空间定量组合异常3D分布图

图4 F4空间定量组合异常3D分布图

图5 F6空间定量组合异常3D分布图

由DEM 图可直观看出：F1元素组合异常3D图起伏形态复杂，组合异常高值集中出现在玄武岩覆盖区，且在北东方向上异常值较高，呈串珠状分布，说明异常地分布受北东向鸭绿江断裂控制，但异常分布同时也受东西方向断层的控制。F2元素组合异常在空间上集中分布在老岭地区，元素组合空间位置单一，与荒沟山铅锌矿床位置重合，属于典型的成矿元素共生组合。F3元素组合异常所表达的Cr、Ni、MgO完全受鸭绿江断裂控制，异常方向与测区主构造线方向一致。呈北东向贯穿整个研究区。F4所表达的元素组合异常为As、Au、Sb异常集中出现在研究区的西南部，即老岭成矿带附近，异常的走向亦呈北东—南西向，异常突起明显，强度较高。异常方向与测区主构造线方向一致。F6所表达的元素组合异常为Bi、Cu、W。在空间分布上起伏形态相对简单，异常集中出现在研究区的南部，异常的走向呈北西—南东向，异常突起明显，强度较高。

4 组合异常空间分布特征

将空间定量组合异常图进行空间迭置，结合元素相关性确定综合异常元素，全区共圈定出组合异常22处，组合异常具有明显的分带性，可分为3个带（图6）：

图6 白山地区地球化学组合异常图

Ⅰ带出现在研究区的东南，临江市蚂蚁河乡到长白县的梨树沟一带，其出露地层主要为玄武岩。组合异常形态不规则，呈东西向展布，其异常带的分布主要受东西向断裂控制。带内出现组合异常10处，异常规模大、强度大，浓集中心明显，元素组合以Co－Mn－Ti为主，与一处异常位置与大横路铜钴矿床吻合。根据异常性质，该带异常揭示此带应为与基性－超基性岩有关的钴矿化、锰矿化和钛矿化的混合带。

Ⅱ带出现在研究区的西南，临江市三道岔—花旗镇一带，其出露地层主要为老岭群。异常呈北东向展布，与该区主干断裂构造—鸭绿江断裂展布方向一致。带内出现组合异常8处，异常规模大，元素组合以 As－Au－Sb为主，仅一处出现 As－Au－Sb－Hg－Pb－Zn组合异常，两组异常在空间上具有较好的叠加性。根据异常性质，该带异常揭示北动向断裂控制的中低温热液成矿元素的聚集过程出现As、Sb矿化。

Ⅲ带出现在研究区中部，湾沟镇—闹枝镇—松树镇一带，其出露地层主要为侏罗系。带内出现组合异常3处，异常规模较小，元素组合为Cr－Ni。该带异常揭示此带为与基性、超基性暗色火山岩类有关的元素聚集过程。

5 结语

（1）白山地区成矿过程存在4种元素定量组合，即：反映偏基性的Co、Ti、Mn元素定量组合；反映低温热液成矿的Pb、Hg、Zn；反映中低温成矿属性的Sb、Au、As元素定量组合；反映中高温成矿的Cu、Bi、W元素定量组合。

（2）上述元素定量组合特征再现了元素间的信息互补关系，反映了成岩成矿过程中地球化学元素的内在组配机制与空间关系，证明了白山地区成矿过程具有多源、多期次成矿特征，由此造成该区地表地球化学元素的不同组合类型。

［1］王瑞廷，毛景文，任小华，等.区域地球化学异常评价的现状及其存在的问题［J］.中国地质，2005，32（1）：168－175.

［2］王学求.矿产勘查地球化学：过去的成就和未来的挑战［J］.地学前缘，2003，10（1）：239－248.

［3］谢淑云，鲍征宇.矩分析法及其在粤北韶关地区金属成矿作用研究中的应用［J］.吉林大学学报：地球科学版，2003，33（4）：443－448.

［4］成秋明.多重分形理论与地球化学元素分布规律［J］.中国地质大学学报，2000，25（3）：311－318.

［5］陈敬周.数字高程模型的生成和应用［D］.太原：太原理工大学，2007.729.

［6］胡昌龙，易燕.数字高程模型DEM 及其显示［J］.黑龙江科技学院学报，2004，14（4）：233－236.

［7］刘小生，刘传立.在Arc／Info中建立和应用数字高程模型［J］.铁道勘察，2004（4）：8210.

［8］J aquet O.Factorial kriging analysis applied to geo2logical data f rom pet roleum exploration［J］.Math Geology，1989（7）：683－691.