复合外挂墙板刚度计算方法的研究

杨 君，李九阳

（1.吉林省通化东昌区市住房和城乡建设局，通化134001；2.长春工程学院土木工程学院，长春130012）

0 引言

复合墙板是由内、外两层钢筋混凝土板中间夹保温材料组成的一种新型墙体材料，适用于框架结构的外围护墙体。该墙板采用工厂预制、现场安装，具有保温节能、质量保证、施工速度快等多项优点，有着广阔的应用前景。为了研发复合墙板的构成，设计复合墙板的截面形式之一为：钢筋桁架穿过保温层，埋置在两层混凝土板中，钢筋桁架连接内、外层墙板形成空间体系，使内、外层墙板共同工作，形成整体。由于复合墙板是由2种性能差别较大的材料组成的复合截面，因此刚度计算理论与普通钢筋混凝土构件有很大的差异。为了研发得到新型复合墙板的刚度计算公式，利用有限元程序对复合墙板进行实际受力模拟分析其变形，结合普通钢筋混凝土弹性薄板的刚度公式，探索了复合墙板的刚度计算公式。

普通钢筋混凝土弹性薄板在均布荷载作用下的最大挠度fmax的计算式为：

式中：B——构件的刚度。

从式（2）中可以看出刚度影响因素有：材料的弹性模量E，泊松比υ，截面计算高度h。对于不同材料组合而成的复合截面墙板，考虑材料刚度不同，挠度公式可假定为：

因此研究的思路是首先按照复合墙板的截面组成，计算出合理的刚度，在此基础上，得到合理的修正系数ξ。

1 复合墙板截面刚度计算

1.1 截面折算高度计算

复合墙板的截面由两层钢筋混凝土和一层保温材料组成，由于材料特性不同，所以计算高度不能用三层板的高度之和，由于保温层通过钢筋桁架混凝土层连接，因此视为组合截面，根据惯性矩I相等的原则将计算截面折算高度h′取1m作为计算单元。首先计算截面的形心位置，之后计算惯性矩，再计算折算高度（h1、h2、h3为截面三层材料的厚度）：

截面的形心位置：

计算惯性矩：

按照惯性矩相等计算折算高度：

则折算高度h′为：

得到折合高度h′的计算表达式后，可以计算不同截面尺寸的试件的h′。

1.2 截面弹性模量与泊松比

复合墙板的截面材料分钢筋、混凝土与保温材料3种，所以弹性模量理论上采用折算弹性模量E′，根据常用高效保温材料聚苯乙烯泡沫塑料板的弹性模量、钢筋弹性模量、混凝土弹性模量计算，钢筋截面积占总面积的比例很小（≤0.02%）可忽略，计算截面折算弹性模量，其中混凝土弹性模量为Ec、苯板弹性模量为EP，折算弹性模量的表达式为：

同理计算截面的折算泊松比。但在有限元分析过程中发现，泊松比的变化对计算基本无影响。所以在刚度计算时仍采用钢筋混凝土的泊松比vc。

则复合墙板的刚度计算式为：

式中：E′——复合墙板的折算弹性模量；

h′——复合墙板的截面折算高度；

vc——混凝土的泊松比。

2 刚度修正

利用有限元程序计算得到均布荷载作用下复合墙板的最大挠度，根据截面性质计算得墙板截面刚度，然后计算修正系数ξ。

2.1 有限元分析试件的挠度

刚度的大小主要与截面构成有关，因此针对不开洞口的复合墙板进行有限元挠度分析。截面组成：两层内、外叶混凝土板，内夹聚苯乙烯泡沫塑料板；构件组成：放置竖向、水平桁架，桁架间距变化体现刚度变化；支座：四点简支在墙板上下边缘1／4处；荷载：水平均布荷载。设计试件工况对照组时，应考虑到截面和构件组成，其区分不同的混凝土板厚度、不同的保温层厚度、钢筋桁架的水平以及竖直间距等因素。针对影响刚度的主要因素设计了2种板型、4组截面尺寸、16个试件利用有限元程序，按照上述截面组成、荷载、支座形式，分析得到16个试件的最大挠度。

有限元计算步骤如下：

第1步，创建模型所需的单元。在ANSYS的Main Menu中选择Element Type，建立2种不同的单元。第1种为体单元，选用Solid concret 65单元；第2种为线单元，选用Link 3Dfinit stn 180单元。

第2步，定义线单元截面特性，在RealConstants的下拉选项中输入钢筋的截面积168（在ANSYS中默认单位为mm2）。

第3步，创建3种材料。在Material Props下拉选项 Models中，定义混凝土、钢筋、聚苯乙烯泡沫塑料的弹性模量、泊松比。

第4步，建模，创建节点、单元，分别形成两层混凝土墙板单元、聚苯乙烯泡沫塑料单元、钢筋桁架、钢筋网单元，复制单元形成墙板。

第5步，给模型加上力学性质。首先给模型加约束，选取4个约束的位置，分别限制X、Y、Z3个方向的移动。然后施加荷载，要注意的是，墙板加载的一面正好是约束位置的反面，对所有节点的加载，模拟均布荷载。

第6步，运算、求解。在Solution选项中执行计算命令，此时程序自动进入运算状态，伴随着自动跳出的模型文本信息，出现“Solution is done！”的命令提示窗口，表示此时模型加载运算已经完成。

第7步，模型加载后处理阶段。在加载运算结束之后，查看模型变形情况，在General Postproc选项的Plat Result菜单选择Contour Plot下的节点变形，查看节点变形中的Z方向变形。

2.2 墙板的刚度值计算及其修正系

根据有限元分析程序计算的挠度最大值和刚度计算值，由式（3）求得修正系数ξ的理论值。

修正系数ξ影响因素有：复合墙板内外叶厚度h1、h3、保温层厚度h2、钢筋桁架间距c、d。将上述组成因素进行无量纲化，得到修正系数ξ的3个构成因子：作为自变量。

将自变量与因变量组成函数分析矩阵，使用Matlab程序回归得出修正系数的公式。

假定ξ计算公式模型为：

利用Matlab一次线性函数回归程序，回归出了方差最小的ξ表达式各项系数：

将回归得出的系数代入式（10），得到ξ的表达式：

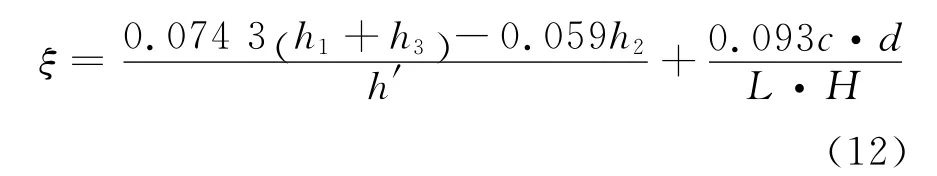
2.3 修正系数ξ的误差分析

将16个复合墙板试件的物理参数代入式（10），得出试件的挠度计算值，将得出的挠度计算值与有限元分析得出的试验值比较。计算所得的挠度值与有限元试验的挠度值平均误差率在5%以内，所以式（10）刚度计算公式具有足够的精度。

3 结语

3.1 挠度计算公式

将修正系数ξ代入式（3），则复合墙板挠度的计算公式为：

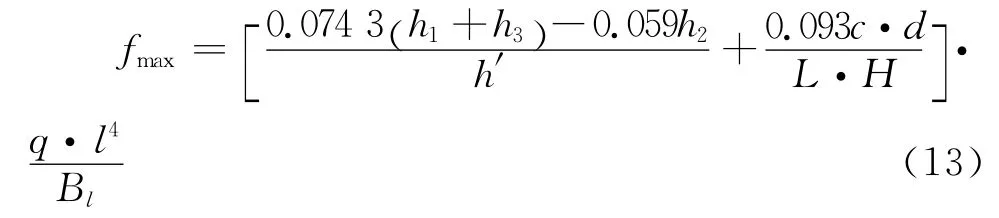
式中：h1、h3—— 分别为复合墙板截面内、外层墙板的厚度；

h2——复合墙板保温层厚度；

c、d——分别为复合墙板钢筋桁架的水平、竖直间距；

h′——复合墙板截面折算高度；

B——复合墙板的折算刚度。

3.2 墙板挠度影响因素分析

对比多组墙板试件的最大挠度数据可以得到影响复合墙板挠度的因素：内、外层墙板的厚度对变形影响最大；其次是钢筋桁架的间距对墙板的变形影响；另外，保温层厚度增大，墙板的变形也减小。具体结论如下：

（1）其他条件相同的复合墙板，内、外层板厚度h1、h3越大，挠度越小；

（2）其他条件相同的复合墙板，保温层厚度h2越大，挠度越小；

（3）其他条件相同的复合墙板，钢筋桁架的间距c或者d越小，挠度越小。

［1］王爱民，姚谦峰，吴敏哲.中高层密肋壁板结构弯剪受力性能有限元分析［J］.工业建筑，2005（10）：20－22.

［2］李九阳，王莹，刘娜.夹芯复合墙板在水平荷载作用下变形的有限元分析［J］.工业建筑，2010，40（12）：87－89.

［3］Jiuyang Li.Finite Element Analysis of Displacement of Composite Wall Cla0dding under Wind Loading［A］.ICETCE.The 1nd International Conference on Electric Technology［C］.Lushan：ICETCE，2011：2261－2264.