稳健估计在水准网数据处理中的应用
陈永星
(郑州市规划勘测设计研究院,郑州450000)
稳健估计是在粗差干扰不可避免的情况下,选择适当估计方法,尽可能地减免参数估值的影响,得出正常模式下的最优或接近最优的参数估值。测量数据受误差干扰是不可避免的,视其误差大小可分为有效数据、有用数据和有害数据3类。能正确揭示其分布模式的为有效数据,虽不是有效数据,但却能反映分布基本特征,对提高参数估值有用,称为有用数据,有害数据指含有粗差的数据。稳健估计原则是充分利用有效数据,限制利用有用数据和排除有害数据。在本文中采用了从一般到特殊的验证方法,选取了独立的水准网,用Matlab编写了选权迭代程序,分别采用Huber法、IGG1法在不含粗差、含有粗差的情况下,进行选权迭代,并和不含粗差、含有粗差的最小二乘估值结果进行比较,比较各种方法的优劣。
1 稳健估计选权迭代法
其计算的迭代过程如下:
(1)选择初始权P(V0),可令各权因子初值均为1,即w1=w2=…=wn=1,W =I,则P,P为观测权阵;
周江文教授1989年提出了不等权独立观测情况下的M估计的法方程写成矩阵形式为

(2)解算法方程(1),得出参数^X和残差V的第一次估值:

2 采用的选权迭代法
2.1 Huber法
Huber提出的ρ函数为:
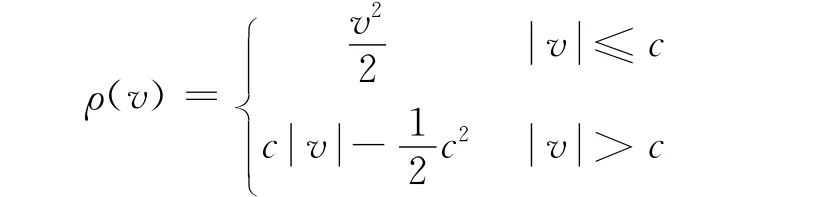
式中c为常系数,通常取c=2σ,相应的权函数为

2.2 IGG法(周江文法)
ρ函数为:

权函数为:
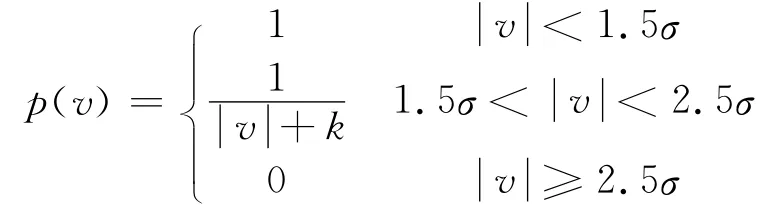
3 水准网观测值的稳健估计
某水准网,共有7个首级控制点,其中A点为已知点。网形如图1所示。

图1 水准网网形图
已知A点高程为HA=31.00m,观测高程为:

取5km观测高差的权为单位权,改正数以mm为单位。从S1~S9其对应的权阵为:
P = diag(1/3,1/4,1/2,1/6,1/6,1/4,1/4,1/3,1)
4 未加粗差时的各种方法平差
控制网采取间接平差法进行平差计算,平差以待定点高程为未知数。利用最小二乘法和稳健估计的选权迭代法对观测数据进行平差。
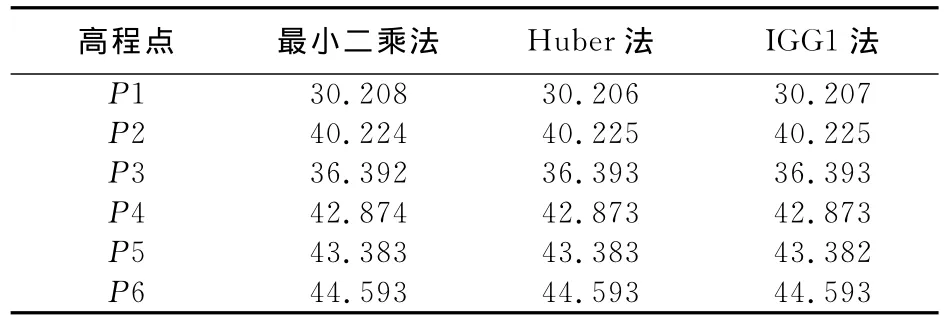
表1 各种方法平差后各个水准点高程值/m
从表1可以看出:在没有加入粗差的情况下,各种平差结果基本一致,都在可接受的范围内,都为正确的值。
5 加入一个粗差后使用各种方法平差
为了说明各种选权迭代法在粗差剔除中的应用,再加上观测路线比较长,在观测数据h6中加入120mm(远大于二倍中误差)的粗差,即观测值为6.601m。然后使用各种方法平差,其平差结果见表2,各路线平差后的权见表3。

表3 加入一个粗差后的各路线平差后的权
从表2可以看出:当观测值加入粗差后,最小二乘平差结果偏离正确值,说明最小二乘抗差较弱;各种选权迭代结果基本一致,都在正确值的范围内,说明稳健估计具有抗差性。
从表3可以看出:Huber法和IGG1法L6的单位权远远小于其余路线的权,可以认为为0。由此可推断,在观测值中含有粗差,这与实际一致。充分说明了Huber法和IGG1法具有发现粗差的能力。
6 加入2个粗差后各种平差结果
在数据中加入2个粗差,然后再用各种方法进行平差,其平差结果见表4,各水准路线平差后的权见表5。
从表4与不含粗差的正确结果比较可以看出:
(1)当加入2个粗差时,最小二乘平差结果大大偏离正确值。
(2)Huber法、IGG1法和正确值相比,都有所偏离,其中IGG1法在整体上与正确结果最为接近。
从表5可以看出:Huber法中只探测出一个粗差,IGG1法的L3、L6的权几乎为0,可以判断出其中含有误差,这与结论相符。
综上所述,在探测粗差时,IGG1法比残差绝对和最小法和Huber法都更优化,具有准确的探测粗差的能力。
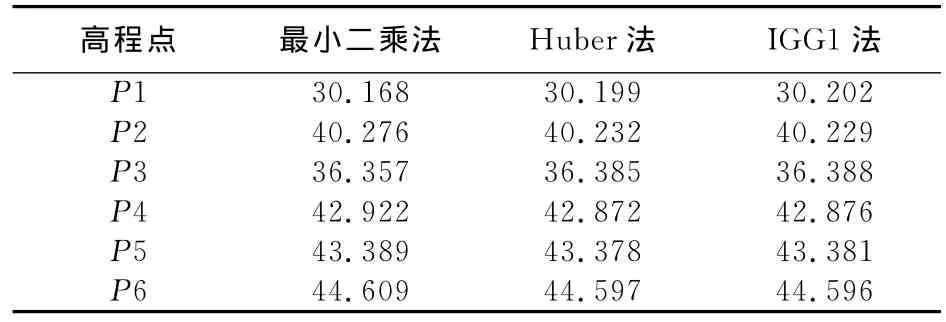
表4 加入2个粗差后的各点高程

表5 加入2个粗差后的各水准路线平差后的权
7 结语
通过本文的一些粗浅的研究,我们可以得出以下结论:
(1)在观测值不含粗差的情况下,最小二乘估计具有最优性,能得到最优的线性解;稳健估计也能很好地估计参数,但得到的解不是最优解。
(2)在观测值含有少量粗差的情况下,最小二乘估计失效,估计结果大大偏离正确值范围,而稳健估计具有良好的抗差性,能很好地进行估计,具有很好抵抗残差影响的能力。
(3)当批量采集测量数据时,在数据中是否含有粗差未知的情况下,不能通过人工剔除粗差,稳健估计具有很好的抗差效果。
[1]周江文,黄幼才,杨元喜,等.抗差最小二乘法[M].武汉:华中理工大学出版社,1995.
[2]陶本藻.测量数据处理的统计理论和方法[M].北京:测绘出版社,2007.
[3]余学祥,吕伟才.抗差估计在粗差探测及测量平差中的应用[J].测绘工程,1996(3):40-44.
[4]P J Huber.Robust estimation of a location Parameter[J].Ann.Math.Statist,1964,35(1):73-101.
[5]H P Shen,Z Y Zhu.Robust estimation of the self-similarity parameter in network traffic using wavelet transform[J].Signal processing,2007,87(9):2111-2124.
[6]S Baselga.Global optimization solution of robust estimation[J].Journal of Surveying Engineering,2007,133(3):123-128.
- 长春工程学院学报(自然科学版)的其它文章
- 数据挖掘技术在井斜控制中的应用
- 框架结构房屋抗震鉴定及加固措施

