电网非理想情况下的双馈风电机组锁相控制

刘昌金 徐 君 陈 敏 徐德鸿

（浙江大学电气工程学院 杭州 310027）

1 引言

在传统化石能源日益紧张和环境污染日益加剧的情况下，开发和利用风能受到了广泛关注。截至2010年，全球累计风电装机容量已接近 200GW，我国达到 44.7GW，成为风电装机容量第一大国。随着风力发电在整个电力系统所占比例越来越大，电网非理想情况下的风电机组并网运行性能成为了研究的重点[1-4]。

双馈风力发电系统的电压定向矢量控制通常基于同步旋转坐标变换，需要准确的电网电压频率和相位信息[5]。在电压畸变、频率跳变、相位突变以及三相不对称等电网非理想情况下，亟须解决的问题是快速、准确地锁定电网电压频率和相位。硬件锁相电路一般依赖于电压信号零点时刻的检测，当电网畸变时，信号零点与基波零点不一致，甚至可能在基波零点附近存在多个信号过零点，且在三相相位不对称时难以分离出正序电压的相位[6]。为此，文献[7,8]采用了一种不依赖于电压信号零点检测的软件锁相方法，但该方法在电网出现谐波和三相不对称时不能很好地跟踪电网的相位和频率。文献[9,10]指出，通过合理设计环路滤波器可有效降低谐波和三相不对称对锁相环路的影响，但又不可避免地降低了锁相环路的动态性能。为了消除三相不对称对软件锁相环路的影响，文献[5]给出了一种基于正、负序旋转坐标变换的双dq锁相方法，该方法需要利用截止频率较低的低通滤波器来提取正、负序分量的幅值，在获得较好稳态性能的同时影响了动态性能的提高。文献[11,12]采用了基于两相静止坐标系的延时信号消除方法来分离出所需正序电压分量，然而该算法并不能消除由于电网的5次正序、7次负序谐波分量而在锁相环路中引入的4倍、8倍工频周期脉动量，限制了锁相环路动态性能的进一步提高。为保证双馈风电机组在电网非理想情况下仍能获得较好的锁相性能，本文在上述研究的基础上，对电网非理想情况时的软件锁相性能进行了分析，从提高锁相环的稳态精度和动态性能方面提出了一种适用于电网非理想情况下的软件锁相控制方法。

2 dq坐标系中的锁相模型

同步旋转 dq坐标系的软件锁相算法如图 1所示，Park坐标变换相当于鉴相器，环路滤波器一般采用比例-积分（PI）控制器，积分环节相当于压控振荡器。图 1中，usa、usb和 usc为电网三相电压，usd、usq分别为 dq坐标系的 d、q轴电压，ω0、ωp分别为锁相环的初始角频率和输出角频率，fp、θp分别为锁相环的输出频率和相位，Gcon(s)为环路滤波器的传递函数。

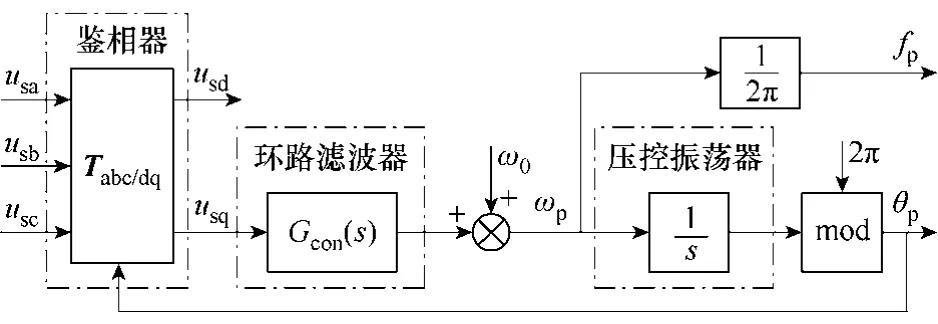
图1 基于dq坐标系的锁相算法框图Fig.1 Block diagram of dq-PLL

若电压为三相对称且不含谐波的理想电网，其三相电压的表达式可写成

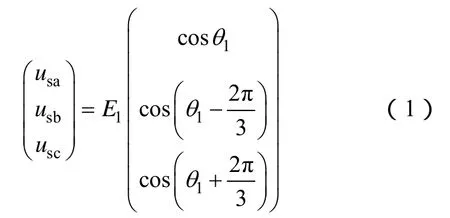
式中，E1、θ1分别为电网相电压的幅值和相位；θ1=ω1t+ φ1；ω1=2 π f1；f1、φ1分别为电网相电压的频率和初相角。经过Park坐标变换得到dq坐标系的电网电压为

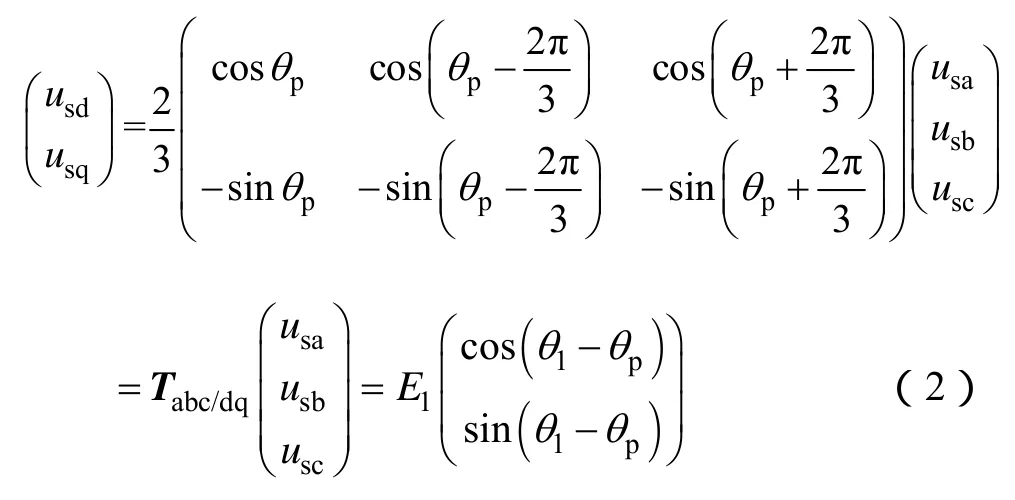
式中，Tabc/dq为三相静止 abc坐标系到同步旋转 dq坐标系的 Park变换矩阵；θp为锁相环输出相位，θp= ωpt + φp；φp为锁相环输出相位的初相角。

当电网相电压的相位与锁相环输出的相位之间的差值较小时，式（2）可近似认为

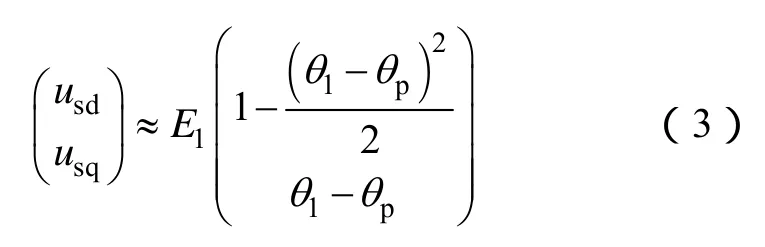
式中，K为鉴相器的增益，K=E1。

由此，可得出基于dq坐标系的软件锁相环的线性化模型，如图2所示。

因此，可用usq来反映相位的误差信息e(t)

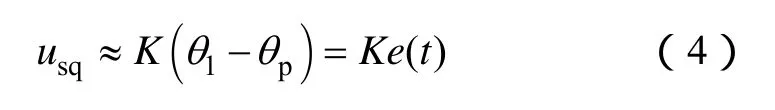
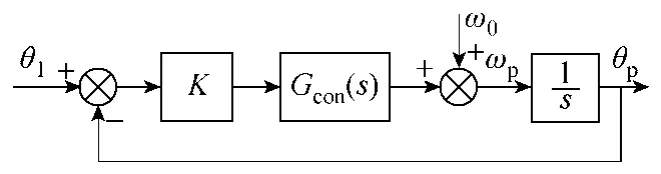
图2 dq锁相环的线性化模型Fig.2 dq-PLL linear model

3 电网非理想情况下的锁相实现

3.1 电网非理想时的锁相分析

电网非理想时，可能的电压质量问题包括电压骤变导致的相位和频率突变、电压畸变以及三相不对称。一般情况下，畸变电网的谐波分量主要为奇次谐波，每相电压为奇谐波函数[13]。当电网电压三相不对称时，基于对称分量法[14]，电网电压可描述为对称的正序电压、负序电压和零序电压的合成。因此，电网非理想时的三相电压可表示为

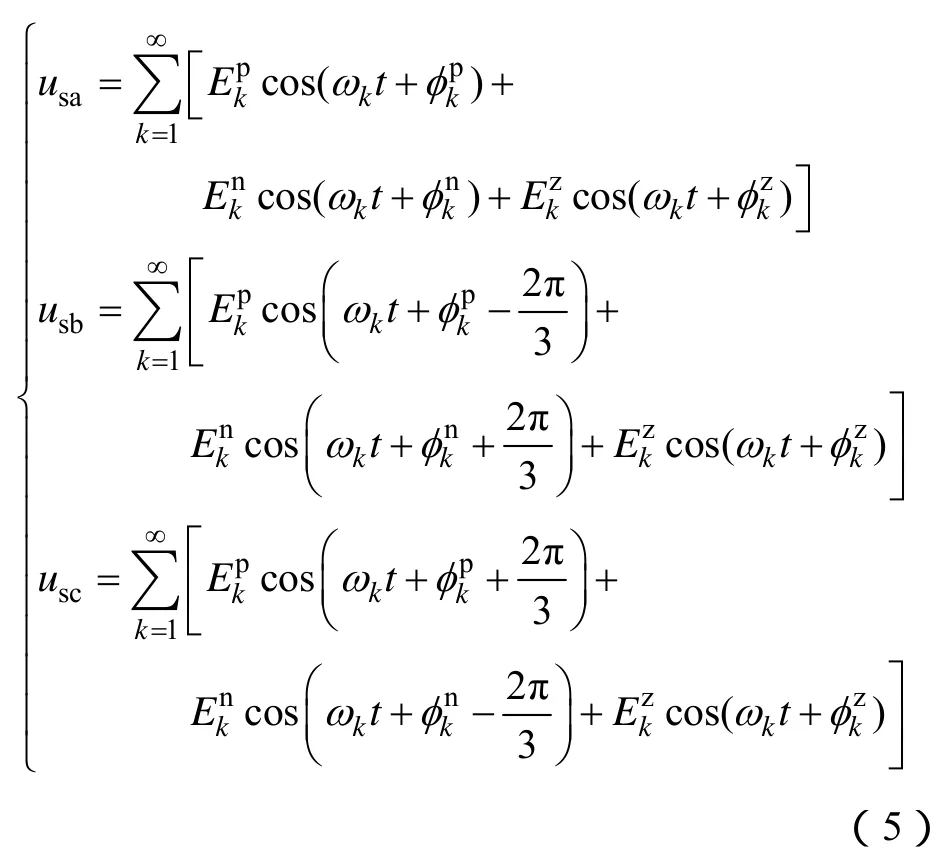
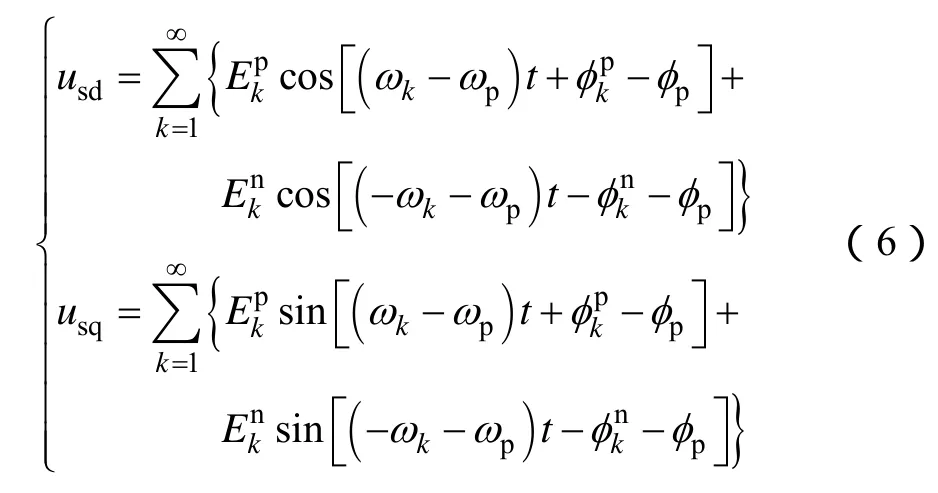
假定锁相环能够跟踪电网相位，从式（6）可知，式（5）中的基波正序分量将转换成直流量，基波负序分量转换成频率为 2f1的交流量，低次谐波成分中的5次负序、7次正序分量转换成频率为6f1的交流量，5次正序和7次负序分别转换成频率为4f1、8f1的交流量。这些低频的交流成分会在锁相环路中引入波动，影响锁相性能，甚至可能导致锁相失败。为了抑制交流成分，通常在锁相环路中串联一个截止频率远低于 2f1的低通滤波器，这使得锁相环的动态响应具有较大的延时，不利于电网发生故障时双馈风电机组并网变流器快速跟踪电网相位。

3.2 基于abc坐标系延时算法的dq锁相方法

为了进一步提高锁相环的动态性能，应增加锁相环路的带宽。然而带宽的增加可能削弱环路对低次谐波的抑制能力，影响锁相环的稳态性能。对于具有低通滤波特性的锁相环路而言，谐波频率越高则其在环路中的衰减系数越大。因此，可提高谐波在环路中的脉动频率来改善锁相环的稳态性能。

文献[14,15]给出了一种基于三相静止坐标系（abc坐标系）的延时信号消除算法分离正、负序分量，最大的延时时间为2T1/3 (T1为基波周期)。为了缩短延时时间，可采用式（7）的改进延时方法来提取基波正序分量

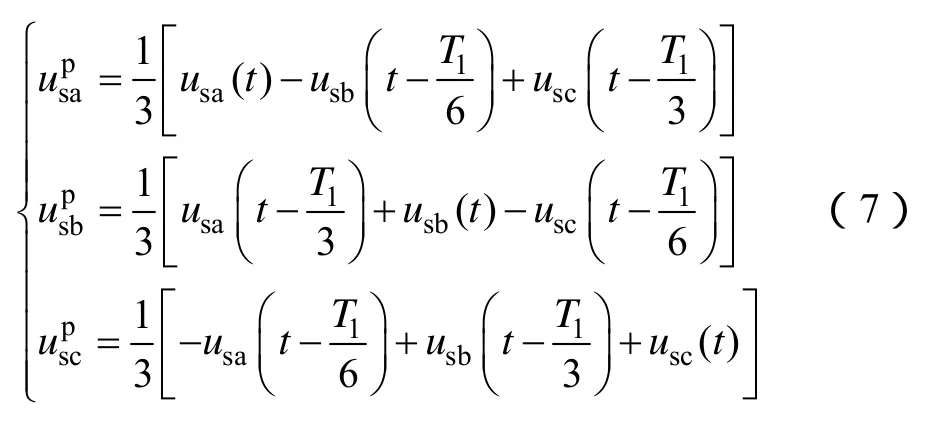
这样，经过T1/3就可以提取出正序分量。将式（5）代入式（7）可得到经过延时算法处理后的三相电压表达式为

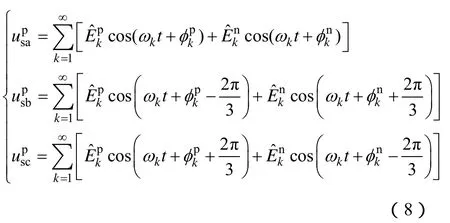
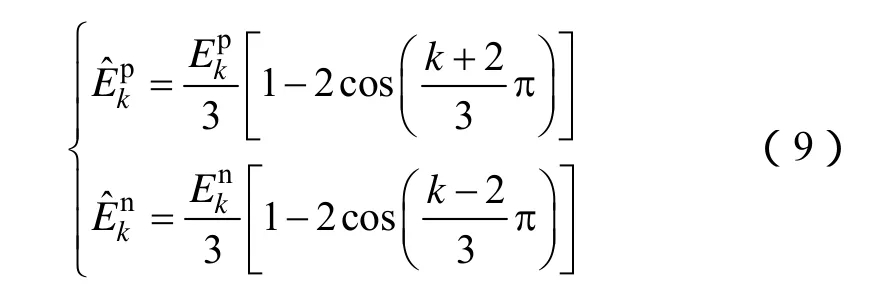
对于式（8）的三相电压表达式，经过 Park坐标变换后，可写出对应于dq坐标系的电压表达式为

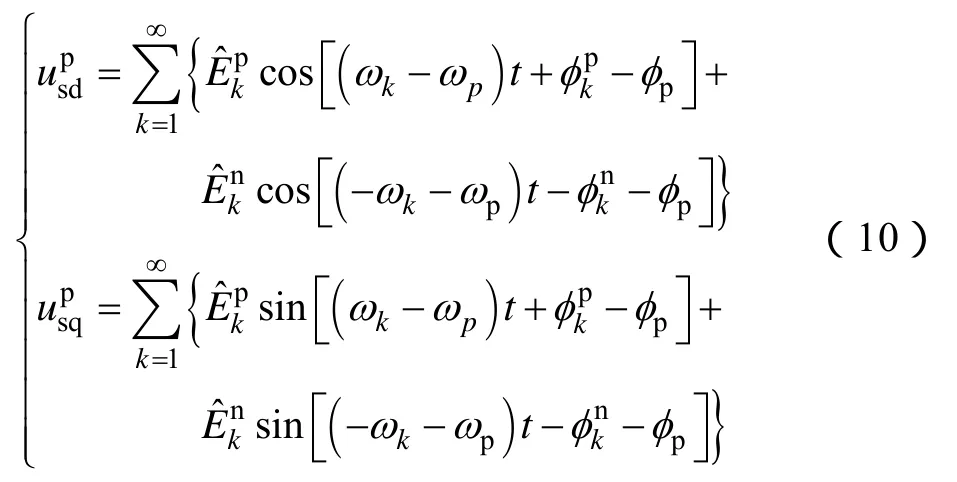
由式（9）可知，采用abc坐标系延时信号消除算法进行正、负序分离后，能够消除因基波负序分量而产生的频率为 2f1的脉动量，也消除了因 5次正序、7次负序谐波成分而引入的频率为 4f1、8f1的脉动量，同时将锁相环路中的最低脉动频率提高到了6f1。在保证锁相环稳态性能的前提下，理论上的环路带宽也可获得提高。基于abc坐标系延时算法的dq锁相控制框图如图3所示。

图3 基于abc坐标系延时算法的dq锁相框图Fig.3 Block diagram of dq-PLL based on abc delay signal cancellation

图3中，采用了截止频率为200Hz的二阶巴特沃斯滤波器来增大锁相环输出频率中可能存在的6f1脉动量的衰减率，Tp为锁相环滤波后的电压周期。

4 设计与分析

为获得较好的锁相精度，环路滤波器可由一阶低通滤波器串联PI控制器组成，其传递函数为

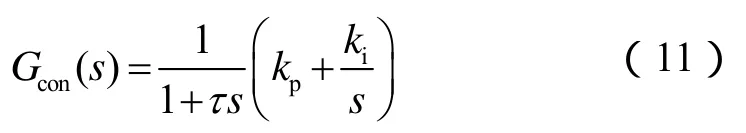
式中，τ 为低通滤波器的时间常数；kp、ki分别为PI控制器的比例、积分系数。为增大锁相环路在6f1频率处的衰减，可设置τ =0.001 6s，使得低通滤波器在300Hz处的获得-10dB的衰减率。

结合图2的锁相环线性化模型，可得到该系统的开环传递函数为

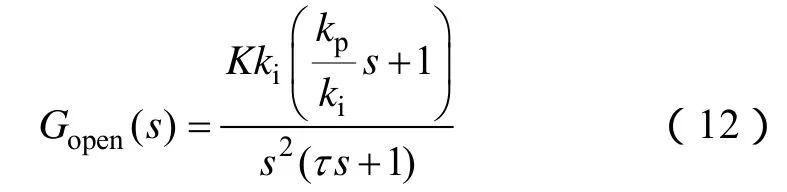
为获得较好的动态性能，设定 Gopen(s)的穿越频率fc为20Hz。为获得较大的相位裕量，可设计零点处的转折频率fT1和极点处的转折频率fT2为

由此，可算出在归一化锁相环路（K=1）的PI控制器参数为：kp=120，ki=800。图 4给出了开环系统的频率特性。从图4a可知，锁相环路在300Hz处的增益为-34dB。

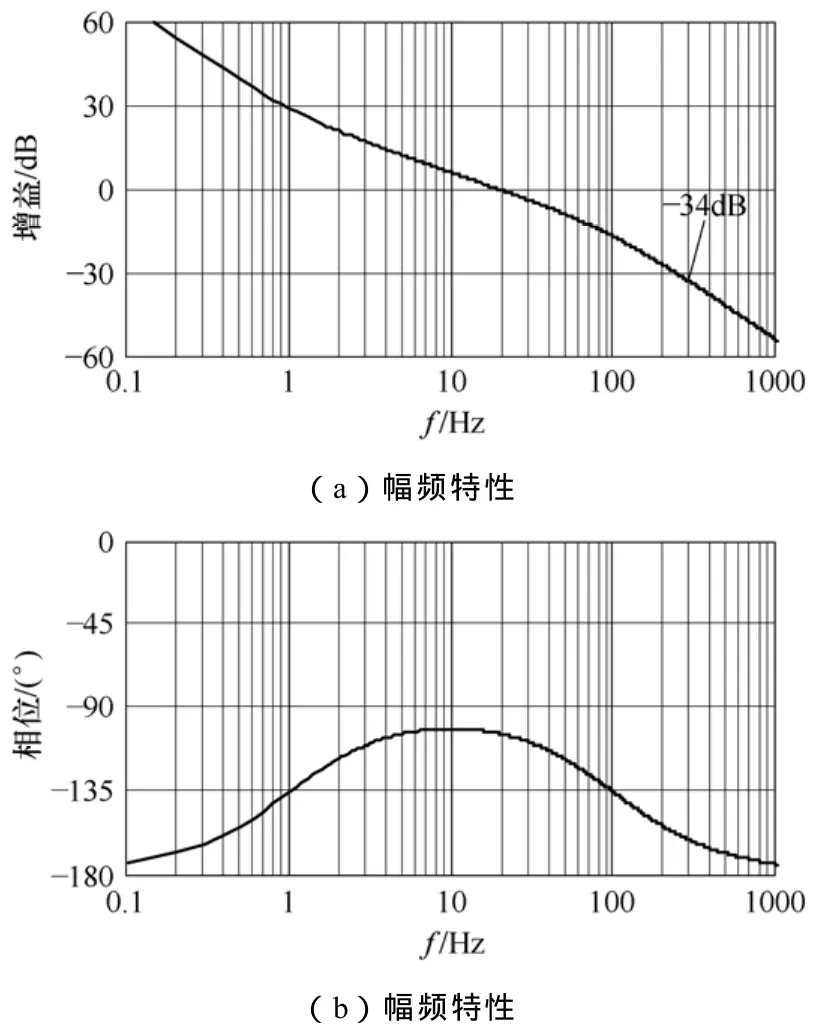
图4 锁相环路开环系统的频率特性Fig.4 Bode plots of PLL open-loop system

5 仿真与实验验证

为了验证在不同电网情况下的基于abc坐标延时算法的dq锁相方法的有效性，进行了实验模拟测试。实验中，主要由可编程交流电源（型号Chroma 6463）来模拟非理想情况时的电网电压，锁相算法由DSP（型号TMS320F2808）实现。单相接地短路故障是电网中最常见的故障，实验中让a相电压跌落80%，造成三相电压之间的不对称，也导致线电压之间出现相位偏移，图5给出了单相跌落时的锁相测试结果。图5a为dq锁相算法输出结果，频率含有由不对称所引入的100Hz波动成分，导致相位存在相应频率分量的波动成分。图 5b为利用 abc延时算法得到的改进dq锁相结果，消除了不对称所导致的频率和相位波动，相位跟踪较好；在a相电压跌落瞬间，频率调节平稳，较快完成了跟踪过程。

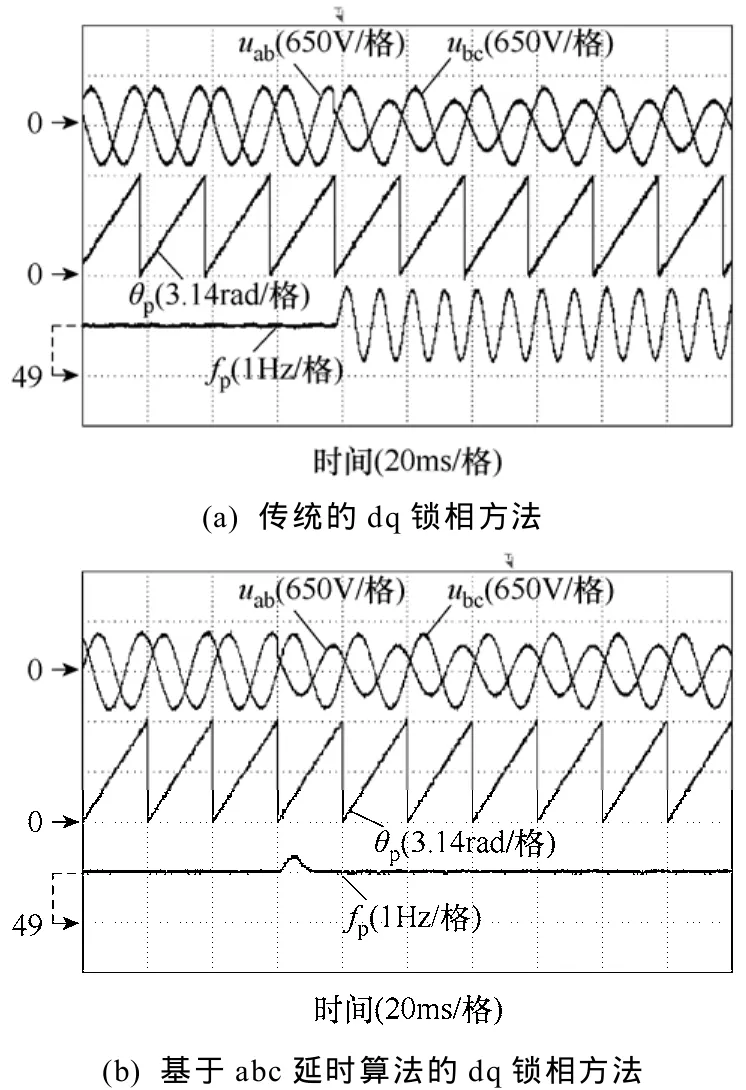
图5 电网从正常到单相跌落80%时的锁相结果Fig.5 Behavior of dq-PLL and improved dq-PLL under 80% voltage drop of phase a

图6给出了三相对称跌落80%时的锁相测试结果。此时传统的dq锁相方法和基于abc坐标延时算法的dq锁相方法都能够很好地跟踪电压相位，频率波动较小，实现了平稳过渡。

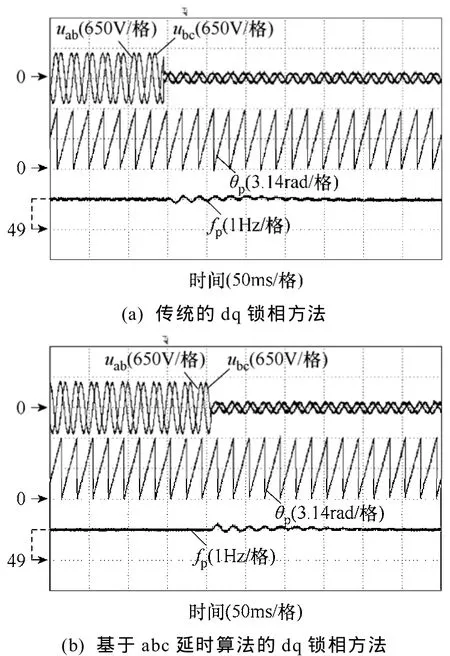
图6 电网从正常到三相对称跌落80%时的锁相结果Fig.6 Behavior of dq-PLL and abc-PLL under 80%voltage drop of three-phase

图7给出了电网发生畸变时的锁相测试结果。由于可编程交流电源尚无谐波注入功能，实验中利用双路数字信号发生器来模拟畸变时电压信号，电压信号直接送给DSP的采样端口，电压信号频谱如图7c所示，谐波次数主要为5次和7次，5次谐波含量为7.0%，7次谐波含量为6.9%，电压总畸变率（THD）为10%。图7a为传统dq锁相方法得到的结果，从图可知，锁相输出存在低频的波动成分。图7b采用abc延时算法后，5次正序和7次负序谐波被滤除，5次负序和7次正序谐波转换成300Hz的波动成分，该波动成分基本由环路滤波器消除，稳态性能较好，如图7b所示。

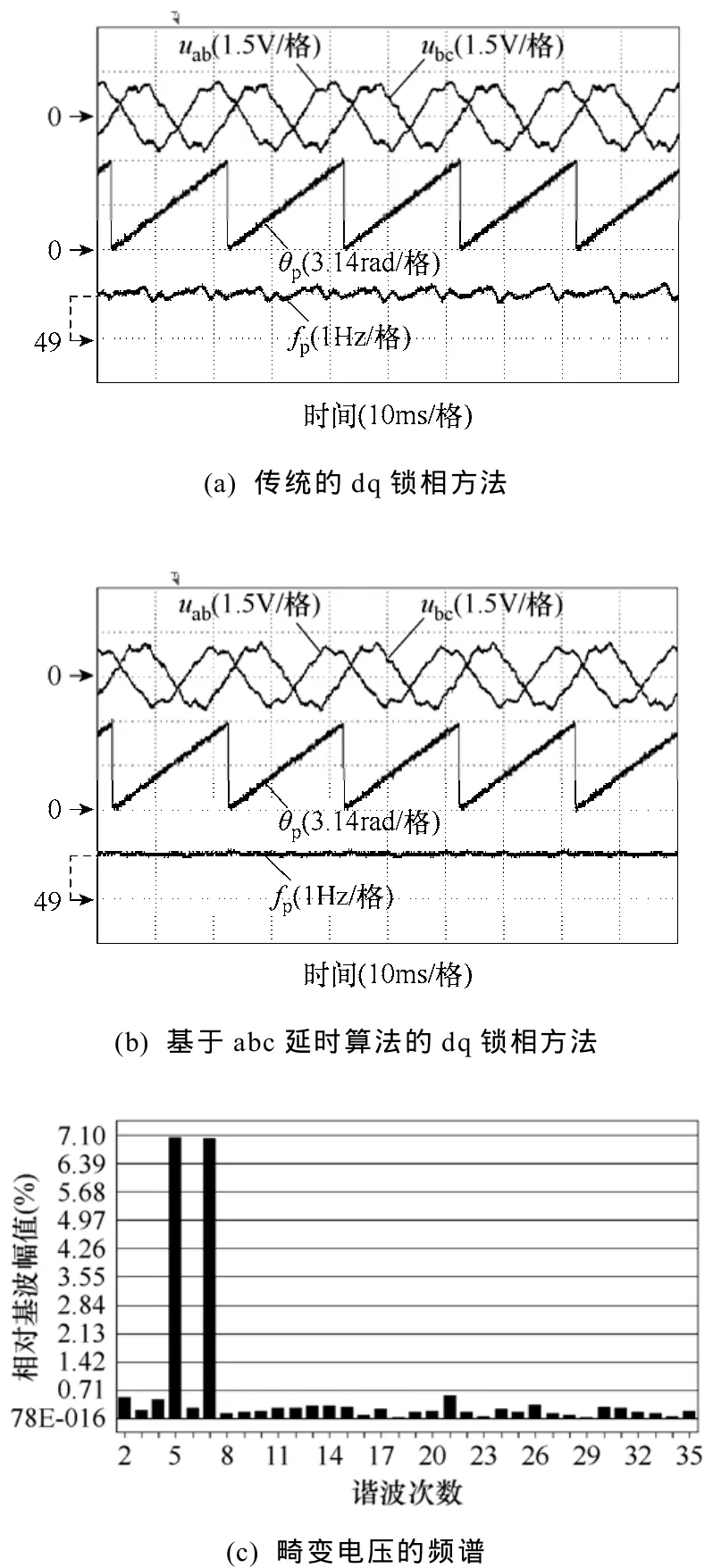
图7 电网畸变时的锁相结果Fig.7 Behavior of dq-PLL and abc-PLL under distortion grid

为了验证基于abc坐标系延时算法的改进锁相方法在同时含有电压畸变、电压跌落和相位突变等电网非理想情况时的相位跟踪性能，进行了仿真测试，结果如图8所示。图8a为注入5次谐波的三相电压波形，THD为7%，在0.1s时刻三相电压对称跌落80%并发生30°的相位突变。经过abc延时信号消除算法提取出的三相电压正序分量在图 8b给出。图8c为锁相环得到的电压相位。图8d为电压初相角的变化曲线，可以看到，该锁相环的输出能够在 0.08s内跟踪上电网电压的相位，具有较快的动态性能，能够满足文献[16]中列出的风电场并网规约（Grid Code）的动态要求。

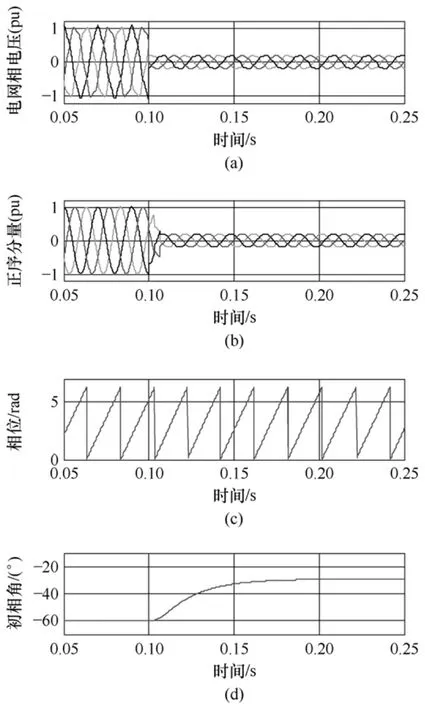
图8 改进dq锁相方法在电网非理想时的动态测试Fig.8 Dynamic behavior of improved dq-PLL under non-ideal grid

图9为改进后的锁相方法与其他两种主要的软件锁相方法的比较。在设计的控制参数（见下表）能够满足相同的稳态性能条件下，让电压频率从50Hz阶跃跳变到 51Hz时的动态性能比较结果如图9所示。由图9可知，改进后的dq锁相方法动态响应速度较快，而传统的dq锁相方法较慢，这是由于传统的 dq锁相方法需要设计较低的环路带宽来抑制由于电网不对称所引入的二倍工频脉动量。

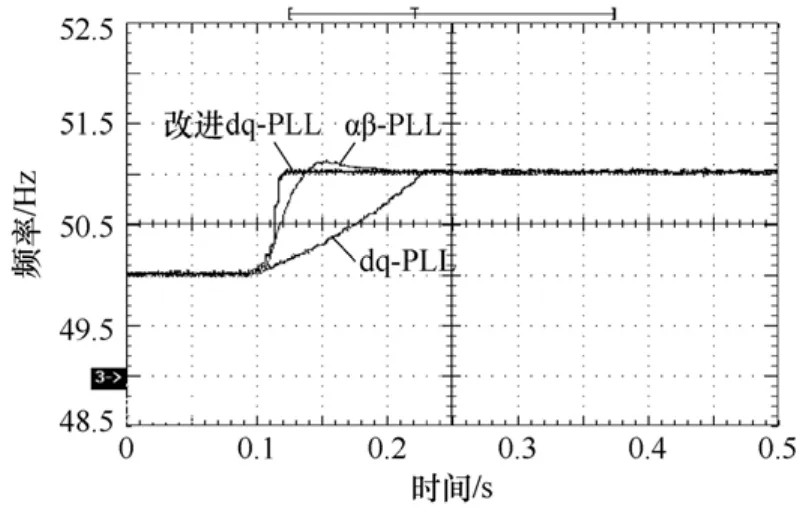
图9 频率突升1Hz时的锁相环动态响应Fig.9 PLLs response after frequency 1 Hz step change

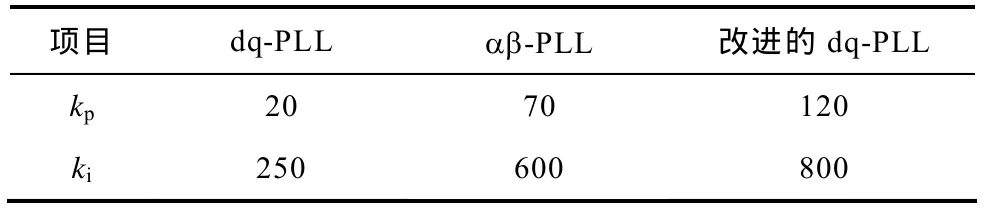
表 几种锁相方法的控制参数Tab. Control parameters of PLLs

图10是本文提出的锁相方法在1.5MW双馈风力发电实验平台上的实测波形。电网中接有较大容量的整流性负载并导致电压畸变，线电压的 THD为10.8%，其中5次为9.6%，7次为2.0%。从图10可以看出，在电网电压畸变较严重时，改进的锁相方法仍能准确跟踪基波相电压的相位。

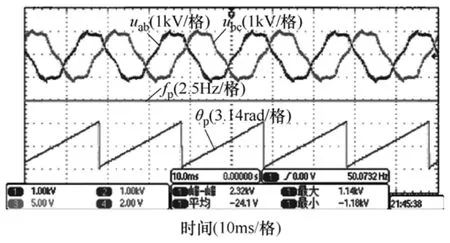
图10 1.5MW双馈风力发电平台的锁相测试波形Fig.10 Improved dq-PLL test in 1.5MW DFIG platform

6 结论

本文分析了电网在非理想情况下对双馈风电机组锁相的影响，提出了基于abc坐标系延时算法的软件锁相方法，锁相闭环控制器采用了一阶低通滤波器串联PI控制器的结构，该控制器增加了高频段的衰减率，给出了控制器参数的设计方法，并进行了仿真和实验验证。结果显示：该软件锁相方法具有较好的频率和相位跟踪性能，不仅抑制了电网三相不对称和畸变所引起的锁相环路的波动，同时也获得了较好的动态性能，能够在电网发生故障时快速地跟踪电网频率和相位，可为电网非理想情况时的双馈风电机组的可靠运行提供准确的电网频率和相位信息。

附 录

给出式（7）～式（9）的推导过程。以a相为例，将式（5）的电网非理想时的电压表达式代入式（7）可得到经过延时算法处理后的a相电压表达式

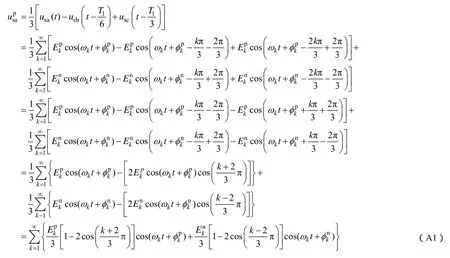
式中，k=2m-1（m=1，2，3，…）。

与之类似，可得到结果延时算法处理后的b相和c相表达式，分别为

[1]贺益康, 周鹏. 变速恒频双馈异步风力发电系统低电压穿越技术综述[J]. 电工技术学报, 2009, 24(9):140-145.He Yikang, Zhou Peng. Overview of low voltage ride-through technology for variable speed constant frequency doubly fed wind power generation systems[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 140-145.

[2]Hu Jiabing, He Yikang, Xu Lie, et al. Improved control of DFIG systems during network unbalance using PI-R current regulators[J]. IEEE Transactions on Industrial Electronics, 2009, 56(2): 439-451.

[3]Xu Lie. Coordinated control of DFIG’s rotor and grid side converters during network unbalance[J]. IEEE Transactions on Power Electronics, 2008, 23(3):1041-1049.

[4]Kiani M, Lee W. Effects of voltage unbalance and system harmonics on the performance of doubly fed induction wind generators[C]. 2008 IEEE Industry Applications Society Annual Meeting, 2008: 1-7.

[5]周鹏, 贺益康, 胡家兵. 电网不平衡状态下风电机组运行控制中电压同步信号的检测[J]. 电工技术学报, 2008, 23(5): 108-113.Zhou Peng, He Yikang, Hu Jiabing. Detection of voltage synchronization signals for a wind energy generation system unbalanced grid conditions[J].Transactions of China Electrotechnical Society, 2008,23(5): 108-113.

[6]周国梁, 石新春, 付超. 三相电压畸变条件下软件锁相环分析与实现[J]. 电力电子技术, 2007, 41(7):47-49.Zhou Guoliang, Shi Xinchun, Fu Chao. Operation of a software phase locked loop under distorted three-phase voltage[J]. Power Electronics, 2007,41(7): 47-49.

[7]Kaura V, Blasko V. Operation of a phase locked loop system under distorted utility conditions[J]. IEEE Transactions on Industry Applications, 1997, 33(1):58-63.

[8]Chung Se-Kyo. A phase tracking system for three phase utility interface inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(3): 431-438.

[9]Zhan C, Fitzer C, Ramachandaramurthy V K, et al.Software phase-locked loop applied to dynamic voltage restorer(DVR)[C]. 2001 IEEE Power Engineering Society Winter Meeting, 2001:1033-1038.

[10]Wu Longhui, Zhuo Fang, Wang Zhaoan. Soft phase locked loop for active power filter applied in small rating stand-alone power system[C]. 2007 IEEE Power Electronics Specialists Conference, 2007:2600-2606.

[11]Saccomando G, Svensson J. Transient operation of grid-connected voltage source converter under unbalanced voltage conditions[C]. 2001 IEEE Industry Applications Conference, 2001: 2419-2424.

[12]Bueno E J, Rodriguez F J, Espinosa F, et al. SPLL design to flux oriented of a VSC interface for wind power applications[C]. The 31th Annual Conference of the IEEE Industrial Electronics Society, 2005:2451-2456.

[13]邱关源. 电路[M]. 4版. 北京: 高等教育出版社,1999.

[14]Rioual P, Pouliquen H, Louis J P. Regulation of a PWM rectifier in the unbalanced network state[C].1993 IEEE Power Electronics Specialists Conference,1993: 641-647.

[15]Rodriguez P, Luna A, Ciobotaru M, et al. Advanced grid synchronization system for power converters under unbalanced and distorted operating conditions[C]. The 32th Annual Conference of the IEEE Industrial Electronics Society, 2006:5173-5178.

[16]Clemens J, Julija M, Thomas A, et al. International comparison of requirements for connection of wind turbines to power systems[J]. Wind Energy, 2005,8(3): 295-306.