连续Petri网的死锁和陷阱结构性态分析*
惠秀 李承家
(杭州电子科技大学理学院)
连续Petri网的死锁和陷阱结构性态分析*
惠秀 李承家
(杭州电子科技大学理学院)
连续Petri网是用来分析和描述具有连续变量的系统,被证明是有效的建模工具。本文主要讨论连续Petri网死锁和陷阱结构的性质,并结合算例对此进行了说明。
连续Petri网;死锁;陷阱;结构性质
1 引言
连续Petri网作为Petri网的一个重要分支,它的概念和相关理论由David[1]等人于1987年首次提出。连续Petri网建模优点是它的库所的标识可以是非负的任意实数,这样可以用连续Petri网近似逼近原型Petri以减少状态数目,从而解决原型Petri网的可达状态爆炸问题。连续Petri网可分为自主连续Petri网(Autonomous Continuous Petri Net,ACPN)和时间连续Petri网(Time Continuous Petri Net,TCPN)[2]。近年来很多学者致力于连续Petri网系统相关的研究,见参考文献[3]、[4]。本文主要研究具有死锁和陷阱结构的连续Petri网的性质。
随着人们对连续Petri网研究的深入,连续Petri网已经在实际领域如生产制造系统、流体系统、转换线系统[5]等得到广泛的应用。这些系统在设计过程中通常要对其性能进行分析和预测,而对系统结构方面性质的分析就更加重要。本文以具有死锁和陷阱结构的原型Petri网为基网,配置任意的库所标识,研究具有死锁和陷阱结构的连续Petri网在运行过程中的拓扑结构性质。
2 连续Petri网的定义及相关概念
本文主要参考文献[7]、[8]的相关概念理论,给出以下的定义:


定义2.2连续Petri网的变迁发生规则:

死锁和陷阱是Petri网系统中两种特殊的库所子集,关于死锁和陷阱的研究已经取得了大量的成果,主要可参考文献[7]、[8]。

在Petri网系统的运行过程中,一个不含有标识的死锁(即死锁中的各个库所的标识数均为0),永远不会得到标识;一个含有标识的陷阱(即陷阱中至少有一个库所含有标识)永远不会失去标识。
3 连续Petri网的性质分析
关于连续Petri网的可达性、有界性、活性、公平性等,文献[5]已经做了相关的论述,文献[6]研究了自主连续Petri网的相关性质以及判定方法。陷阱和死锁结构是Petri系统的拓扑结构性质,下面主要给出具有死锁和陷阱结构的连续Petri网的一些性质。性质3.1 设是一个连续Petri网,N={p,t;F}是其基网(其中p是非空有限库所集;t是非空有限变迁集;F是流关系),N'是N的逆网,P⊆P1。那么有:
(1)1P是网N的一个死锁当且仅当1P是N'的一个陷阱;
(2)1P是网N的一个陷阱当且仅当1P是N'的一个死锁。


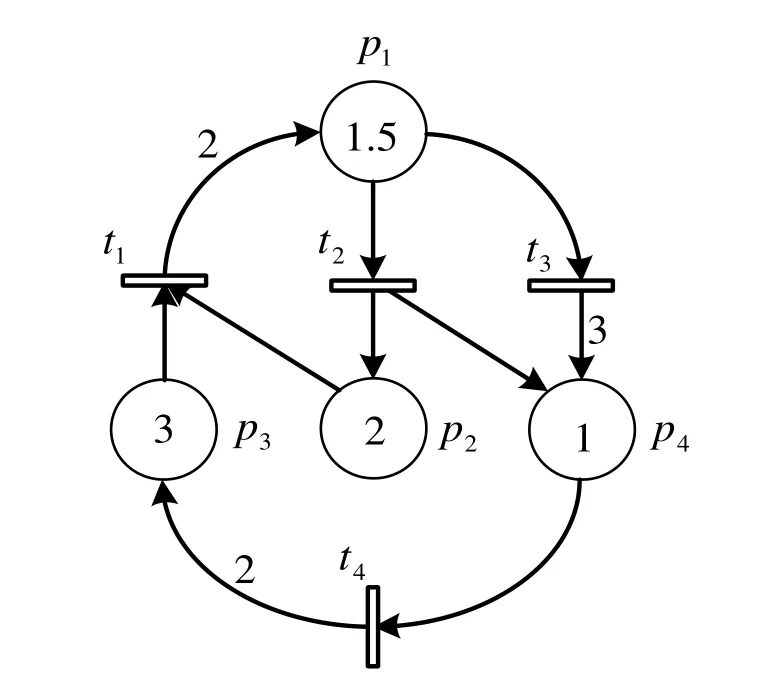
图1 具有死锁的连续Petri网R1

图2 连续Petri网R1的逆网
4 实例分析
图1的连续模型{p1,p2}为一个死锁,配置任意的初始标识,根据连续Petri网的运行规则,变迁分别以相应的发生量先后发生,得到如图3的一个状态演变图。从3图可看出存在一个m0的可达状态m1,其标识为在此状态下,m1的任意可达标识均有而验证了性质3.2 (1)的正确性。

图3 网系统R1的演变图

图4 网系统R1的逆网的演变图
5 结论
本文根据连续Petri网的运行特点,分析了具有死锁和陷阱结构的连续Petri网的性质,发现其与基网的性质保持一致,这对连续Petri网的性质研究有很重要的意义,尤其是对连续Petri网的活性等方面的研究具有很深远的意义。今后很重要的一个研究就是分析具有死锁和陷阱结构的连续Petri网的活性。
[1] R David, H Alla. Continuous Petrinets, 8th European Workshop on Applications and Theory of Petrinets[M]. Saragosse(E), 1987:275-294.
[2] R David, H Alla. Autonomous and Timed Continuous Petrinets, Advance in Petrinets[M]. G.Rozenberg Ed, Springer-Verlag, Berlin, 1993:71-90.
[3] J Julvez, L Recade, M Silva. Steady state performance evaluation of continuous mono-T-semiflow Petrinets[J]. Automatica ,2005, 41 (4): 605-606.
[4] 廖志文,文瑛,王汝凉.一类区间速率连续Petri 网的可达稳态分析[D].系统仿真学报, 2005:44-47.
[5] Isabel Demongodin, Mustapha Mostefaoui, Nathalie Sauer, Steady state of Continuous Neutral Weighted Marked Graphs[M], IRCCyN. 2000:3189-3194.
[6] 赵义军.自主连续Petri网的性质及判定方法[D].山东矿业学院学报(自然科学报),1999:89-92.
[7] 吴哲辉.Petri网导论[M].北京:机械工业出版社, 2006:88-89.
[8] Rene David, Hassane Alla. Discrete, Continuous, and Hybrid Petri nets. [M]. Springer , 2010:117-130.
The Structure Analysis of Continuous Petri Nets with Deadlock or Trap
Hui Xiu Li Chenjia
(Science College, Hangzhou Dianzi University)
Continuous Petri nets are widely used to analyze and describe the system with continuous variables. It is proved to be an effective modeling tool. This paper discusses the structure properties of the continuous Petri nets with deadlock or trap. An example is presented to illustrate the properties of the continuous Petri nets.
Continuous Petri Nets; Deadlock; Trap; Structure Property
惠秀,女,1986年生,硕士在读,研究方向:不确定控制系统的理论与应用。
国家自然科学基金资助项目(60934009)

