桥式试件微动疲劳寿命预测与试验研究

潘容，崔海涛，杜文军

桥式试件微动疲劳寿命预测与试验研究

潘容1，崔海涛2，杜文军1

(1.中国燃气涡轮研究院，四川成都610500；
2.南京航空航天大学能源与动力学院，江苏南京210016)

对钛合金桥式试件进行数值分析与微动疲劳试验研究，提出了用MSWT参数预测裂纹萌生位置的方法和基于MSWT参数的微动疲劳寿命预测模型。试验结果与断口分析表明：疲劳裂纹出现在微动试件的接触区边缘，与MSWT参数预测的裂纹萌生位置一致。利用桥式试件的微动疲劳试验数据，获得了寿命预测模型中的相关参数，并采用相关文献中燕尾榫连接结构的试验结果对该预测模型进行了验证。

MSWT参数；裂纹位置；寿命；钛合金

11 引言

航空发动机上相当多的构件(如压气机/涡轮的榫连接、盘轴安装边连接等)都存在着微动磨损，且因微动磨损引发的构件疲劳断裂事故多次发生。因此，在设计这些关键件时，其微动疲劳失效受到广泛重视。航空发动机的风扇/压气机盘和叶片通常采用钛合金制造，而钛合金对微动疲劳很敏感，极易发生微动疲劳失效事故。因此，针对长寿命、多次重复使用的航空动力装置，研究其易发生微动疲劳损坏的结构并采取相应的抗疲劳措施，对保障飞行安全十分重要。英、美等国从20世纪中叶开始研究微动磨损并提出了一系列理论。随着分析、测试技术的发展，人们不断揭示出微动运行机制和损伤机制之间的内在规律。国内北京航空航天大学主要研究了钛合金在常温、高温下的微动疲劳及其防护工艺，南京航空航天大学对航空发动机叶片和轮盘榫连接结构也进行了微动疲劳研究。

本文对钛合金桥式试件进行了微动疲劳理论分析与试验研究，提出了用MSWT参数预测裂纹萌生位置的方法，并验证了基于MSWT参数的微动疲劳寿命预测模型，可为航空发动机中榫连接等接触结构的抗疲劳设计与故障分析提供技术储备。

2 桥式试件的微动参数

桥式试件主要针对燕尾榫连接接触疲劳进行模拟，其中微动试件模拟发动机工作叶片榫头，微动垫模拟发动机轮盘榫槽，如图1所示。微动试件为普通疲劳试件，其中间两面分别放置微动垫。试验时微动试件承受一交变载荷(轴向载荷F)，微动垫在法向载荷(法向力P)作用下紧压在微动试件表面，从而使微动试件和微动垫在接触区域发生微动，同时产生摩擦力(剪切力Q)。

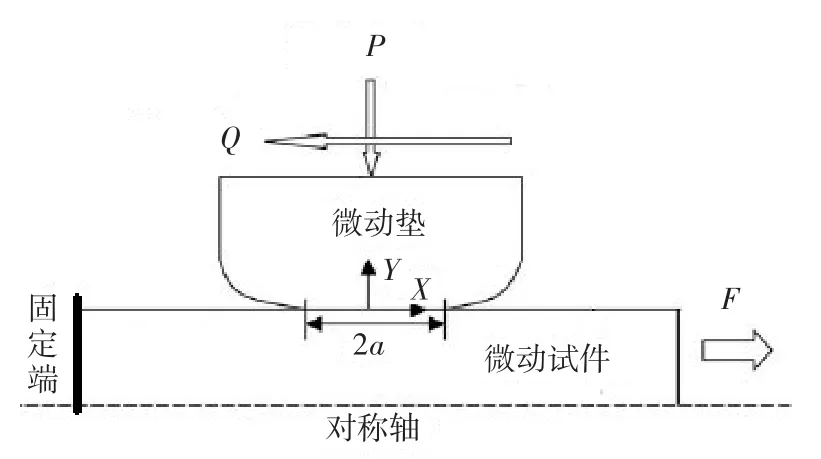
图1 桥式试件结构示意图Fig.1 Bridge-like specimen configuration

2.1 试验件及试验载荷

微动试件和微动垫的材料均为钛合金TC11，密度为4.48 g/cm3，室温下的材料性能[1]为：弹性模量E=120 GPa，泊松比μ=0.3，拉伸强度σb＝1 130 MPa，屈服强度σ0.2＝866 MPa。微动试件和微动垫的几何尺寸如图2所示。

图2 桥式试件几何尺寸(mm)Fig.2 The size of bridge-like specimen

试验载荷状态水平和试验件数量见表1，其中轴向施加载荷比R=0.1的低周载荷。

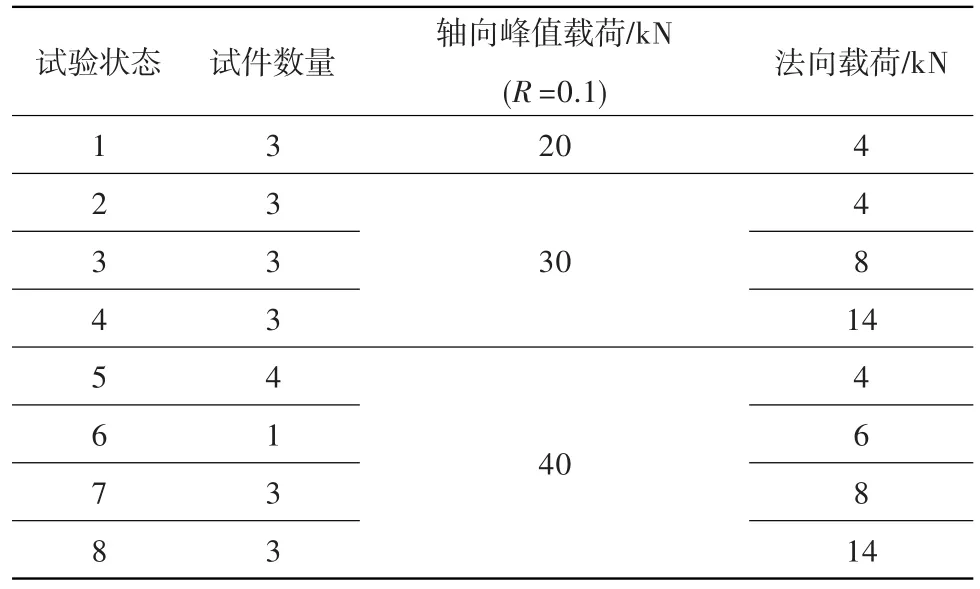
表1 试件数量和试验载荷水平Table 1 Specimen amount and test loading

2.2 微动参数分析

微动试件及微动垫的有限元模型如图3所示，单元为带厚度的8节点四边形单元PLANE82。选择目标单元TARGE169和接触单元CONTA172在接触面上建立接触对，施加约束和载荷进行求解。

图3 有限元模型Fig.3 Finite element model

模拟试验状态3的载荷，有限元分析时在微动垫顶部均布法向载荷，在微动试件一端均布轴向载荷，另一端固支。接触区域微动垫网格单元长50 μm，微动试件网格单元长40 μm，摩擦系数取0.5。微动接触副在试验状态3下的应力分布如图4、图5所示。

由图4可见，接触区最大等效应力为871 MPa，主要由法向载荷传递到微动试件上引起，出现在接触区两边缘，距接触中心约2.56 mm。最大接触压力位置(见图5)与最大等效应力的一致，以接触中心为对称点沿整个接触区域呈马鞍型对称分布，两边高、中间低。

根据临界面法[2]得出试验状态3下MSWT参数在接触区的分布示意图(如图6)，MSWT参数的表达式[2]为：

图4 P=8 kN、F=30 kN时等效应力图(MPa)Fig.4 Von Mises stress(P=8 kN,F=30 kN,MPa)

图5 P=8 kN、F=30 kN时挤压应力云图(MPa)Fig.5 Contour of pressurization stress(P=8 kN,F=30 kN,MPa)

图6 MSWT参数在接触区域的分布规律Fig.6 Curve of MSWT parameter in contact region

式中：σmax为峰值载荷下接触区某节点对应的最大等效应力；σmin为谷值载荷下接触区同一节点对应的最小等效应力；Δεa为循环应变幅；m为材料参数[3]，对于钛合金，m取0.45。

从图6中可知，桥式试件接触区域的微动参数与等效应力的分布规律也一致，在接触区两边缘最大，此处可能为裂纹萌生位置。本文对TC11/TC11接触副在其余7种微动疲劳试验状态下也进行了数值分析，表2为8种状态下接触区MSWT参数的最大值，各状态下参数最大值均出现在接触区边缘。

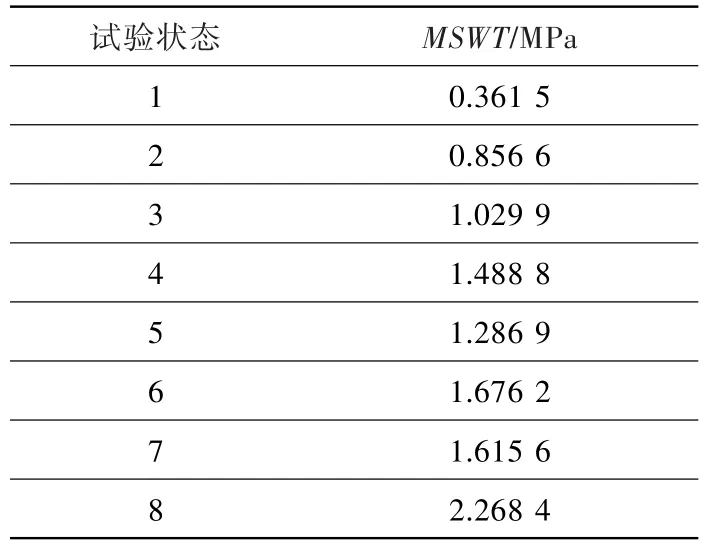
表2 各试验状态的MSWT参数最大值Table 2 The maximum of MSWT at various test conditions

3 桥式试件微动疲劳试验

3.1 试验原理

微动疲劳试验的加载方案[4]如图7所示。整个机械部分通过前后左右4块连接角铁依托在SDS50型电液伺服动静万能试验机的两侧立柱上，微动试件装夹在试验机夹头中。微动垫装夹在微动垫夹持器中，在微动试件的左右侧各布置一个。夹持器底座通过螺栓连接在横向加载装置平台上，与整个加载装置形成整体，保证微动垫夹持紧固。试验时，液压缸两侧的活塞杆伸出压紧微动垫夹持器，使微动垫顶紧在试验机上，实现法向载荷加载。

图7 加载设备Fig.7 Loading equipment

3.2 试验结果

共完成了8种状态、23套试件的微动疲劳试验。微动疲劳寿命是根据目视可见裂纹(一般长度为1～2 mm)即停止试验的循环数。裂纹均出现在微动试件上的接触区边缘，试件的裂纹位置如图8、图9所示。

图8 疲劳裂纹位置示意图Fig.8 Fatigue crack location

图9 微动试件断裂照片Fig.9 The photo of fretting specimen fracture

结合前文数值分析结果及试验表明，MSWT参数预测的裂纹萌生位置与试验中观测到的裂纹位置(即接触边缘附近)基本一致，采用MSWT参数可有效预测裂纹的萌生位置。表3给出了各试验状态下的微动疲劳平均试验寿命，图10为根据表3中数据作出的微动疲劳试验寿命与载荷的关系曲线。从图10(a)可以看出，轴向载荷为30 kN时，随着法向载荷的增加，微动疲劳寿命先减小后增加，这可能是由于单种载荷下的试样数偏少、疲劳寿命分散度偏大所致；轴向载荷为40 kN时，随着法向载荷的增加，微动疲劳寿命逐渐减小且变化速率相对于轴向载荷为30 kN时更快。从图10(b)可以看出，在相同的法向载荷作用下，随着轴向载荷的增加，微动疲劳寿命减小，且法向载荷越大，微动疲劳寿命随轴向载荷的增加减小得越快。

表3 各试验状态下的微动疲劳平均试验寿命Table 3 The average fretting fatigue life at various test conditions

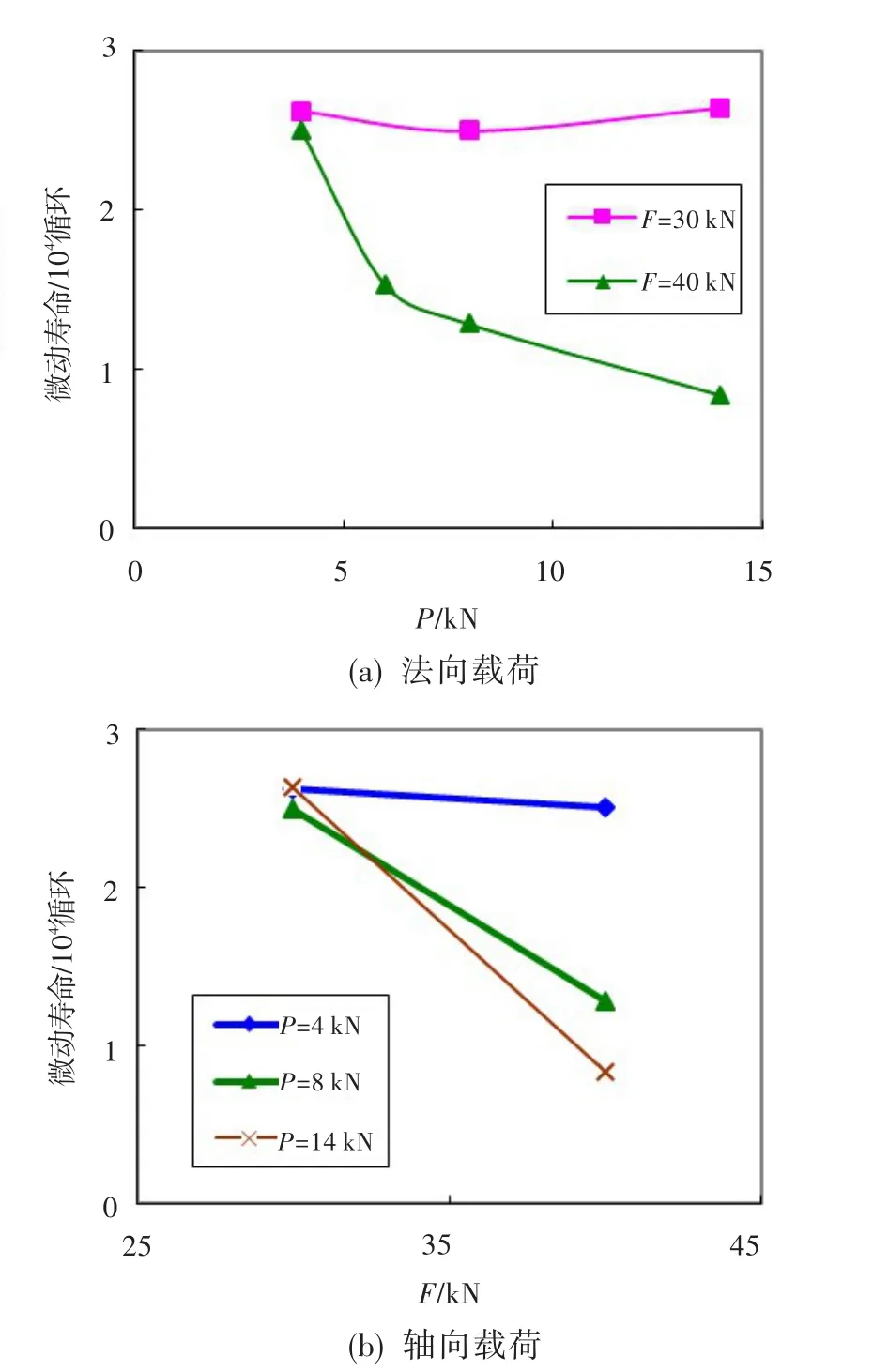
图10 微动疲劳寿命与载荷的关系曲线Fig.10 Curve of fretting fatigue life vs loading

3.3 断口分析

桥式微动疲劳试验的裂纹均出现在微动试件上(如图8、图9所示)，而微动垫由于刚性较大没有出现裂纹。试验过程中，由于微动试件和微动垫之间的摩擦，引起材料表面摩擦系数、表面粗糙度等物理特性发生变化，微动作用造成微动垫接触区材料出现掉屑和剥落现象。对法向载荷为8 kN、轴向载荷分别为30 kN和40 kN的2根试样拉断后进行断口对比。将试件裂纹萌生位置置于最下方，对断口进行显微拍照，同时拍摄相应区域的断口特征，照片如图11、图12所示。

图11 裂纹萌生区域Fig.11 Crack initiation region

图12 裂纹扩展区域Fig.12 Crack propagation region

目视裂纹萌生区域可以发现，疲劳源区断口形貌比较平坦、光亮，且呈半圆形或半椭圆形，长度约2 mm，与试验的停止条件(目视观测到1～2 mm裂纹)相对应，为典型的疲劳断口。裂纹萌生区域颜色发暗(对光的反射能力很弱)，为典型的韧性断裂断口。疲劳断口呈多源性，且疲劳源发生在微动试件表面。裂纹扩展主导方向明确，次裂纹在周边附近。

4 微动疲劳寿命模型的验证

根据试验寿命结果，对文献[2]提出的基于MSWT参数和Coffin-Manson公式[5]的微动疲劳寿命预测模型进行拟合：

式中：σf′为材料疲劳强度系数，b′为疲劳强度指数，εf′为疲劳延性系数，c′为疲劳延性指数，N为疲劳寿命(以循环数计)，n1和n2为寿命常数。

室温下TC11的σf′＝1 578 MPa，b′＝-0.08，εf′= 1.12，c′=-0.85。对式(2)中n1和n2进行拟合，可简化为：

式中：m1和m2为寿命常数。根据式(3)和表2中MSWT参数的分析结果，采用表3中8个状态的试验数据对式(3)进行拟合，拟合曲线如图13所示。由此可得到m1和m2的值，则基于MSWT参数的微动疲劳寿命预测模型为：

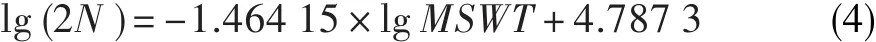
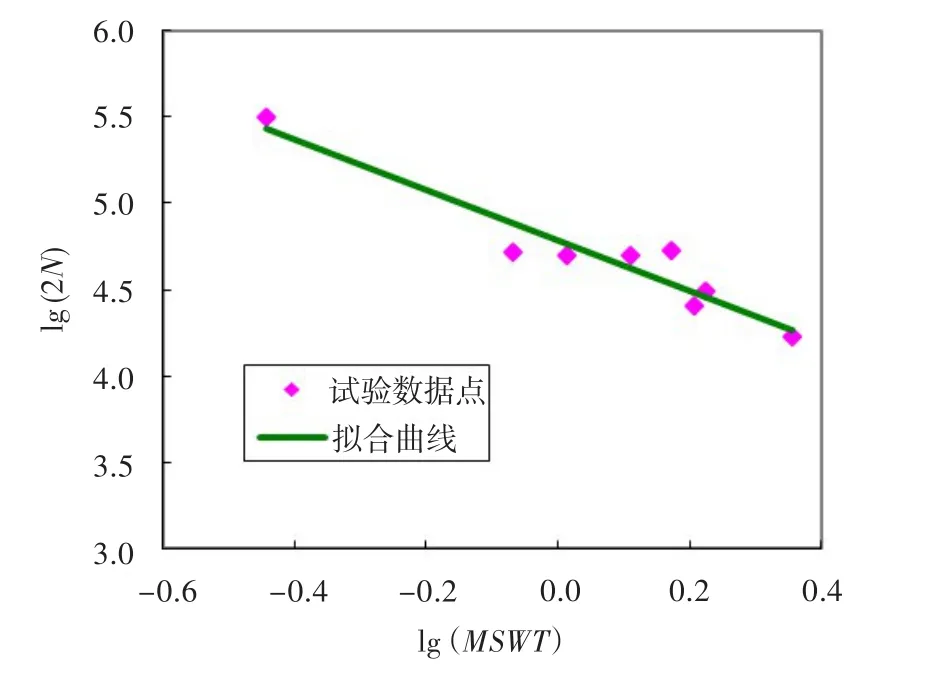
图13 寿命预测拟合曲线Fig.13 Fitted curve of life prediction

利用式(4)对文献[6]中燕尾型榫连接试验件在3种低周载荷下的微动疲劳寿命进行预测，结果如表4所示。从表中可以看出，基于MSWT参数的寿命预测模型对文献[6]中燕尾榫试验件微动疲劳寿命的预测误差分布在80%以内，且预测寿命小于试验寿命，这对发动机榫连接设计而言偏安全。

表4 燕尾榫连接试件寿命预测值与试验值的对比Table 4 The comparison between predicted life and test life of dovetail joint

5 结论

(1)试件裂纹均出现在微动试件上的接触区边缘，且微动试件断口属典型的疲劳断口。

(2)MSWT参数预测的裂纹萌生位置与试验中观测到的裂纹位置基本一致。

(3)利用燕尾榫的微动疲劳试验数据对基于MSWT参数的微动疲劳寿命预测模型进行了验证，且预测寿命小于试验寿命，这对航空发动机榫连接设计而言偏安全。

[1]中国航空材料手册编辑委员会.中国航空材料手册第4卷——钛合金铜合金[K].2版.北京：中国标准出版社，2001.

[2]潘容，古远兴.微动疲劳寿命预测方法研究[J].燃气涡轮试验与研究，2009，22(2)：13—17.

[3]Lykins C D，Mall S，Jain V K.Combined Experimental–Numerical Investigation of Fretting Fatigue Crack Initia⁃tion[J].Int.J.Fatigue，2001，23(8)：703—711.

[4]崔海涛.桥式微动疲劳试验研究[D].南京：南京航空航天大学，2009.

[5]Shin K.Role of Plasticity on Fretting Fatigue Behavior of Ti-6Al-4V[R].AFIT/DS/ENY/04-05，2004.

[6]古远兴，温卫东，崔海涛.燕尾榫连接结构低周微动疲劳寿命预测[J].应用科学学报，2007，25(5)：531—534.

Fretting Fatigue Life Prediction and Test Investigation of Bridge-Like Specimens

PAN Rong1，CUI Hai-tao2，DU Wen-jun1
(1.China Gas Turbine Establishment，Chengdu 610500，China；2.College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

The numerical analysis and fretting fatigue tests for titanium alloy bridge-like specimens have been made.A modified Smith-Watson-Topper(MSWT)parameter approach which is used to predict crack initiation location and the fretting fatigue life model are brought up.The test results and fracture observation show that the fatigue crack origin was located in the contact boundary of the fretting specimens,which was identical with the initiation location that was predicted by the MSWT parameter.Relative parameters in the life prediction model were achieved through the data of bridge-like specimen fretting fatigue tests.Experi⁃mental results of dovetail joint presented in the literature were used to show validity of the proposed model.

MSWT parameter；crack location；life；titanium alloy

V231.95

A

1672-2620(2012)02-0043-06

2011-07-07；

2012-03-28

潘容(1981-)，女，四川泸州人，工程师，硕士，主要从事航空发动机强度寿命研究工作。