地下水位上升对房屋基础沉降影响分析——以绰斯甲水电站水库蓄水对蒲西集镇房屋基础沉降影响为例

陈绪刚，马俊琳，吉 翔

(中国水电顾问集团成都勘测设计研究院，四川成都 610072)

水库蓄水后将引起库岸附近地下水位上升，地下水位上升对建筑物基础沉降变形有较大影响，但目前尚无文献对地下水位上升后，基础沉降变形的影响因素进行系统的阐述和分析。本文从指导基础沉降计算的《地基基础设计规范》公式［4］出发，对影响基础沉降的附加应力、自重应力、压缩模量进行了分析，并以绰斯甲水电站水库蓄水后水位抬升对蒲西镇原有建筑物基础沉降的影响进行了实例分析，最后得出了对工程实践有用的结果。

1 地下水位上升对土体应力变化的影响

1.1 地下水位上升引起基底应力变化

据地基基础规范［4］第5.3.5条推荐的沉降计算公式如下所示。

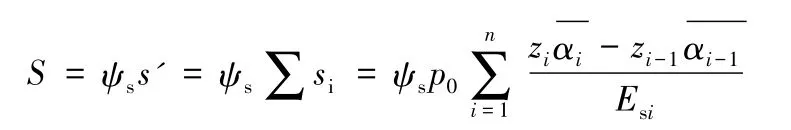
地下水位上升，高度在基础底面以下时，基底附加应力变化:

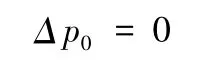
地下水位上升，假定上升至m 土层顶面，高度在基础底面以上时，基础底面土层为第i－1 层。则:

地下水位上升，高度在基础底面以上时，基础以下土层附加应力变化量为:

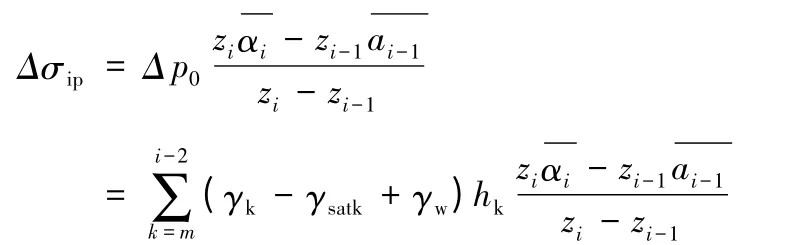
式中:Δ p0为基底附加应力变化量;p为建筑物在基底附加应力;γw、γk、γsatk分别为水密度，第k 层土体重度、土体饱和重度;hk为第k 层土厚度;Δσip为基底下i 土层附加应力变化量。

1.2 基础底面下土自重有效应力变化

Δσit为土体自重状态有效应力变化。

1.3 地下水位上升总应力变化

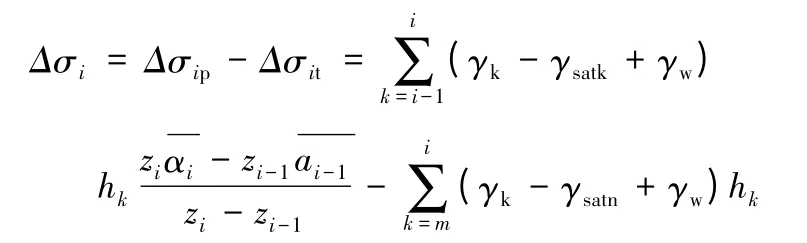
Δσi为i 层土体总应力变化量。

从上述公式可以看出:当地下水位上升但未淹没基础时，基底净附加应力不会改变，Δσip为0，Δσit减小变化量为正值，所以Δσi＜0。当地下水上升至基础底面以上时，基底附加应力将增加，Δσip大于0，Δσit减小，Δσi需根据计算确定。

2 地下水位上升对土体压缩模量的影响

2.1 水位上升对地基土承载力及压缩模量影响定性分析

(1)地下水位上升，由于地下水的浮力作用，土体的有效应力会降低，因此地下水降低将会减小地基承载力;

(2)地下水位上升，将使水位以下的土由于失去毛细管应力或弱结合水形成的表面凝聚力，使地基承载力下降;

(3)地下水位上升，将减小土体的内摩擦角，对砂土尤其明显，这也将使土体的地基承载力降低。

由于土体压缩模量与土体承载力具有正相关性，压缩模量将减小，土体沉降量增加。

2.2 从土体压缩模量与其它物理指标的相关关系分析

根据文献［2］的研究结论，比贯入阻力对土体压缩模量影响显著，但浅层地下水位上升对静力触探试验比贯入阻尼影响不大，所以从Es与土指标的相关性来讲，地下水位上升与Es大小没有必然的联系。

2.3 根据e－p 曲线分析

《建筑地基基础设计规范》［4］公式中的压缩模量是土的自重压力与附加压力之和的压力段进行计算。由于水位上升，土体的自重压力减小，自重应力与附加应力之和也就减小。在压缩曲线上不同压力段的量值是不同的，一般压力较小时，曲线较陡，土体易于压缩;压力较大时，曲线趋于平缓，土体不易于压缩。所以，在地下水位上升时，压力减小，土体变得易于压缩，土的压缩模量将减小。

由于从理论上较难推导水位上升引起Es的变化幅度，因此根据土力学中压缩模量的计算公式，从e－p 曲线着手，讨论地下水位上升引起土体有效应力变化，从而对土体压缩模量产生影响。e－p 曲线参见图1 所示。

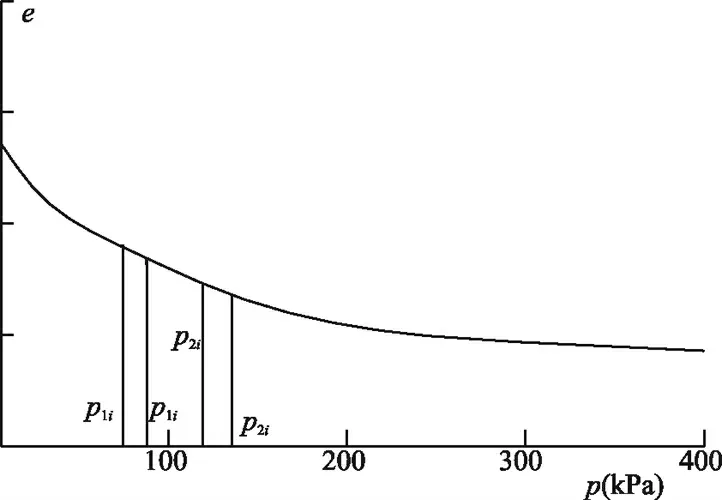
图1 e－p 曲线

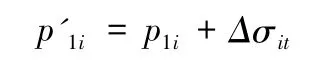
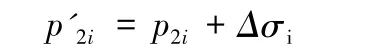
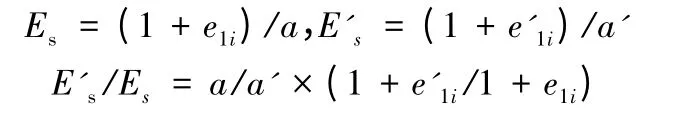
3 地下水位上升对土体应力和压缩模量的实例分析

3.1 蒲西集镇地质概况

蒲西集镇位于四川省绰斯甲河绰斯甲水电站上游，河流多年平均水位2787.31～2787.58 m。绰斯甲水电站水库正常蓄水位为2788.32～2788.51 m，洪水位为2788.8～2789.21 m。水库蓄水后将引起地下水位上升，对原蒲西集镇临河部分建筑及建筑基础有浸没影响，需对已建建筑物基础变形进行分析。

根据四川省绰斯甲河绰斯甲水电站蒲西集镇堤防工程地质勘探报告，其典型地质剖面的相关参见表1 所示，粉质黏土层e－p 对应参数表参见表2 所示。蒲西集镇建筑多为砌体，带地下室，基础为条形基础，基础宽度1 m，埋深－7.5 m，基底持力层粉质黏土，主要压缩土层为粉质黏土层。

基础原地下水位为－11.100 m，该地下水位为多年河流，平均水位2787.31 m，假定在水位未上升时基底附加应力为150 kPa。

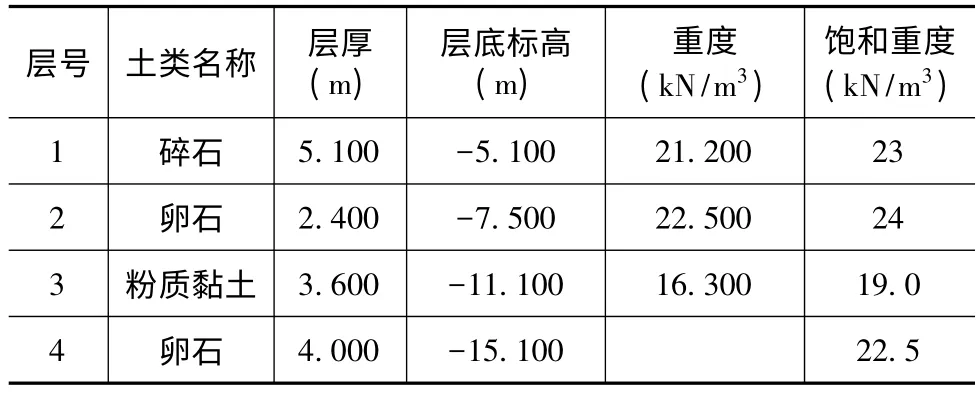
表1 典型地质剖面

表2 粉质粘土e－p 对应表

3.2 土体应力及压缩模量变化规律分析

随着地下水位上升，自重应力变化量、附加应力变化量和总应力变化量如图2 所示，土体压缩模量变化量如图3所示。

由图可知，随着地下水位上升，粉质黏土层自重应力逐渐减小;在地下水位上升到基底之前，基底附加应力不变，土层附加应力也不变，当地下水位上升到基底以上时，基底附加应力增大，土层附加应力增大;粉质黏土压缩模量随着地下水位上升逐渐减小，当地下水位上升达6 m 时，压缩模量变化率不超过15%，表明地下水位上升对粉质粘土压缩模量影响不大。

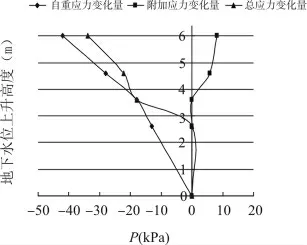
图2 自重应力、附加应力和总应力变化量

4 结论

(1)地下水位上升但未淹没基础时，基底净附加应力不会改变，Δσip为0，土体自重应力Δσit减小，其变化量为正值，所以Δσi＜0。当地下水上升至基础底面以上时，基底附加应力将增加，Δσip大于0，Δσit减小，总应力变化量Δσi需根据计算确定;

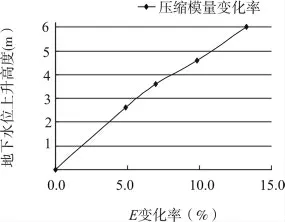
图3 压缩模量变化率

(2)根据e － p 曲线定性分析，一般压力较大时，曲线较陡，土体易于压缩，压力较小时，曲线趋于平缓，土体不易于压缩。在地下水位上升时，压力减小，土体变得易于压缩，土的压缩模量将减小;

(3)根据压缩模量计算公和e －p 曲线，推导了地下水位上升后和地下水位上升前的压缩模量比公式，由于a = Δe/Δ p，为割线斜率，且e － p 曲线走势较缓，应力变化对压缩系数的影响不大，一般情况下a ＞a'。据e －p 曲线e'1i＞e1i和压缩模量比计算公式，E's与Es之比值大小需结合工程实例进行分析并得出结论;

(4)以蒲西集镇地下水上升对房屋基础应力及压缩模量影响为例进行分析，结果表明，随着地下水位上升，持力层粉质黏土自重应力逐渐减小;在地下水位上升到基底以前，基底附加应力不变，土层附加应力也不变，当地下水位上升到基底以上时，基底附加应力增大，土层附加应力增大，但总应力变化量仍为负，这与地下水下降土层有效应力总是增加这一基本规律是一致的;粉质黏土层压缩模量随着地下水位上升逐渐减小，当地下水位上升达6 m 时，压缩模量变化率不超过15%，表明地下水位上升对粉质黏土压缩模量影响不大。

［1］杨建新，李发菊，陈田华.地下水位上升对浅基础地基承载力的影响［J］.基础工程设计，2010(5):95－99

［2］杨红禹，石振明.土压缩模量预测回归分析方法［J］.上海地质，1997(3):44－48

［3］李根义.地下水对地基沉降计算的影响评价［J］.地下水，2009(4):25－26

［4］GB 50007－2002 地基基础设计规范［S］

［5］周健，屠洪权.地下水上升对浅基础地基承载力的影响［J］.港口工程，1994(1):21－24

［6］杨红禹，石振明.未来海平面上升对上海地区激化地基变形预测及其对市政建设的影响［D］.同济大学，1998

［7］上海市水利局海平面上升课题组.未来上海地区海平面上升预测及对策研究［R］.1999