重型轧辊磨床头架主轴顶尖组件的有限元分析

蔡国英

（上海机床厂有限公司 上海 200093）

重型轧辊磨床头架主轴顶尖是直接承受工件重力以及顶持反作用力的重要组件，顶尖和工件依靠中心孔内锥面的接触，来保证工件中心与头尾架中心的一致性。对于不同重量的工件，所使用顶尖的角度以及顶紧力是不一样的。如何对这两个技术参数进行选择，长期以来都是在现场按照经验数据来解决的。利用Pro/E软件子模块Pro/MECHANICA对头架顶尖进行有限元分析，可以在产品设计之初就能得到相关的数据，用来指导磨床的生产和制造。

1 建立几何模型

首先采用软件 Pro/ ENGINEERING建立重型轧辊磨床头架主轴顶尖组件的几何模型。在建立几何模型时，考虑到工件顶持在头尾架中间，头尾架的顶尖的受力情况呈对称型，在建立几何模型时，为了加快运算速度，分析时只取工件的一半进行分析。利用Pro/E软件子模块Pro/ ENGINEERING建立起顶尖与轧辊工件的几何模型，如图1所示。

图1 头架主轴顶尖组件几何模型

2 建立物理模型

建立好几何模型后，在设置好头架主轴顶尖组件的物理属性、边界约束条件和载荷之后就可以进入求解器进行有限元分析求解，计算头架主轴顶尖组件模型的应力和应变。建立一个由顶尖弹簧压力、螺栓预紧力、顶尖锥面过盈配合量及摩擦力、轧辊工件自重、中心孔之间的摩擦力进行综合考虑的物理模型，如图2所示。

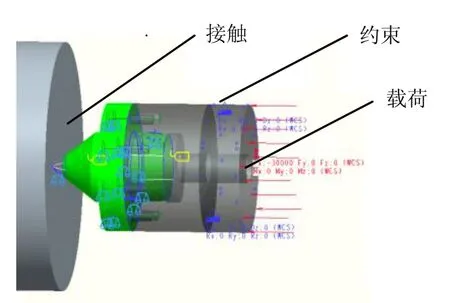
图2 头架主轴顶尖组件物理模型

3 头架主轴顶尖组件的分析结果

计算完成后，在Pro/MECHANICA后处理窗口中，就可以提取计算结果，查看到头架主轴顶尖组件及各个零部件的应力、应变等分析结果。头架主轴顶尖在工作状态下的变形情况如图3所示。

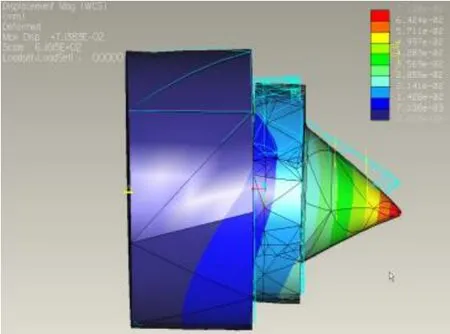
图3 头架主轴顶尖组件变形图

从图3中可以看出，在头架主轴顶尖组件的工作状态中，由于受到工件重量和负载的联合作用，顶尖与顶尖套之间会出现间隙，顶尖中心与理论中心之间产生误差，这样就会造成工件旋转精度的降低。

1)头架顶尖角度

头架顶尖的角度是头架顶尖的一个技术参数，其大小决定了头架主轴在工作状态时二 负载在径向和轴向上的分力。在实际运用中，通常采用60º和75º两种形式的顶尖。当工件重量为73 t时，轴向过盈为0.25 mm，顶尖角度为60º，顶尖接触孔的接触长度为1/4全长时，随着顶紧力的不同，顶尖与顶尖套之间间隙的具体数值见表1。

表1 60º 顶尖变形量

当工件重量为73 t时，轴向过盈量为0.25 mm，顶尖角度为75°，顶尖接触孔的接触长度为1/4全长时，随着顶紧力的不同，顶尖与顶尖套之间间隙的具体数值见表2。

表2 轴向过盈量为0.25 mm时75°顶尖变形量

从表1、表2中可以看出，当工件为73 t，其他技术参数相同时，75º的顶尖较 60º顶尖的上部顶点处的间隙量变小，而上部顶点的过盈量都在增大。相对而言，在头架主轴顶尖组的工作状态中，角度为75º的顶尖的变形量更小。

2)轴向过盈量的影响

在头架主轴顶尖组件中，顶尖与顶尖套依靠1:10的锥度定中心，为了保证装配后的几何精度，两者之间1:10锥度采取过盈配合，如图4所示。在实际运用中，为了便于测量，采用锥度大端直径处的轴向过盈量表示锥度配合的过盈程度，当过盈量分别取值为0.25 mm 、0.15 mm、0.2 mm时，该参数对顶尖变形量的影响见表3和表4。

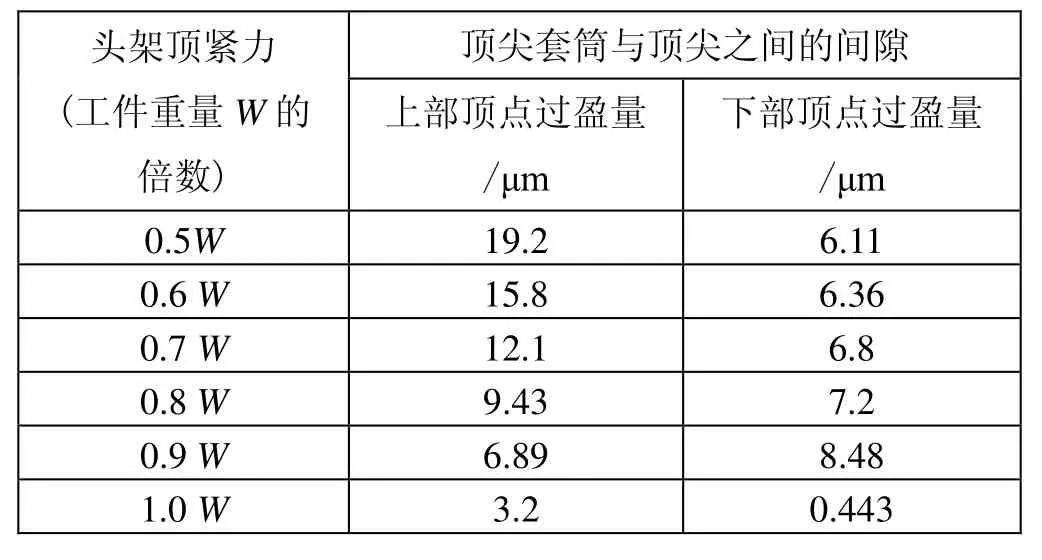
表3 轴向过盈量为0.15 mm时75º顶尖变形量

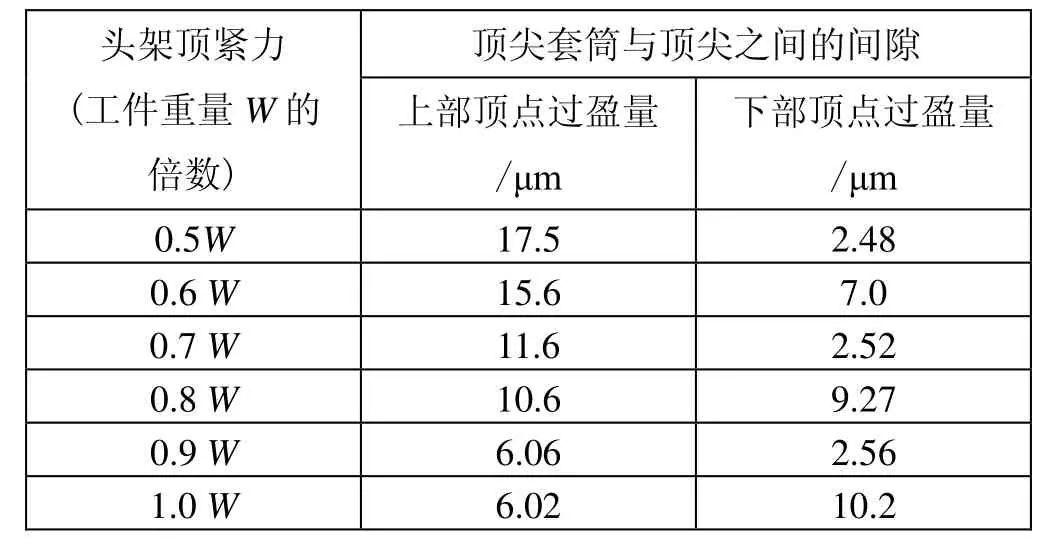
表4 轴向过盈量为0.20 mm时接触长度为全长的 1/4时75°顶尖变形量

当工件为73 t，在其它参数相同时，顶尖上部顶点间隙量与上部顶点过盈量和轴向过盈量并不呈线性关系。轴向过盈量为0.2 mm时，顶尖上部顶点间隙量与上部顶点过盈量和径向过盈量最小。

图4 顶尖上部顶点的间隙和下部顶点的过盈配合

3)顶尖中心孔的接触长度的影响

顶尖轴心孔与工件的接触长度决定了工作状态时工件重量在顶尖上的分布区域、顶尖受力部分面积的单位载荷的大小，决定了工作状态时顶尖的强度及变形量。

在其它技术参数相同情况下，当顶尖与工件中心孔的接触长度分别为全长的1/3和1/4，在这两种情况下顶尖的变形量如表4、表5所示。

表5 轴向过盈量为0.20 mm时接触长度为全长的1/3时的顶尖变形量

从分析数据可以看出，顶尖与工件中心孔的接触长度为全长的1/3时，顶尖的变形量较小。

4 头架主轴顶尖组件的优化方案

从以上分析可以发现，顶尖角度、顶尖的预紧力、轴向过盈量和顶尖中心孔的接触长度这4项技术参数会影响头架主轴顶尖的变形。

综合以上各个影响因素，当工件为 73 t时，采用75º 顶尖、轴向过盈量为0.2 mm、顶尖中心孔与工件长度为全长的 1/3、顶紧力为工件重量时，顶尖的变形量为最小，具体数值是顶尖上部间隙量为2.09 μm，下部过盈量为 2.48 μm。

5 结语

通过对重型轧辊磨床头架主轴顶尖组件的有限元分析，综合得出头架主轴顶尖组件的优化方案。在选择设计变量时，确定目标函数，通过大量的灵敏度分析可以找到影响头架主轴顶尖组件刚度的主要因素，即顶尖角度、顶尖的预紧力、轴向过盈量和顶尖中心孔的接触长度。最终通过各技术参数的优化配置，将顶尖的变形量减小到2.09 μm，比原始设计精度提高了10倍。

[1]孙靖民, 梁迎春, 陈时锦.机械结构优化设计[M].哈尔滨: 哈尔滨工业大学出版社, 2004 .

[2]陈奕.机械结构优化研究与实践[J].组合机床与自动化加工技术, 2007(6): 35−38 .

[3]丛明, 房波, 周资亮.车-车拉数控机床拖板有限元分析及优化设计[J].中国机械工程,2008,19(2):207−213.

[4]徐燕申, 张学玲.基于FEM的机械结构静、动态性能优化设计[J].西南交通大学学报,2003, 38(5):517−520.

[5]翟静, 黎新.机械优化设计综述[J].机械2006增刊,2006(33): 4−5.

[6]杨英,赵光耀,孟凡亮.某轿车白车身结构灵敏度分析及结构优化[J].东北大学学报(自然科学版),2008,29(8): 1159−1163.

[7]叶勇,朱若艳.基于有限元分析的结构优化设计方法[J].机械, 2004, 31(11): 18−20 .