一种新型自复位防屈曲支撑的拟静力试验

刘 璐 吴 斌 李 伟 赵俊贤

(哈尔滨工业大学土木工程学院，哈尔滨150090)

防屈曲支撑构件是应用于多高层结构中的抗侧力耗能减震装置，在中震或大震作用下，防屈曲支撑构件在拉压时均能实现全截面充分屈服而不出现支撑构件的整体或局部屈曲破坏，使原来通过主体结构梁端塑性铰的耗能方式转变为只在防屈曲支撑部件上集中耗能，从而较好地保护了主体结构［1-2］.

然而，防屈曲支撑构件通过钢材的弹塑性来耗能，导致其在经历大震后产生较大的残余变形.强烈地震使结构产生的过大侧向变形及残余变形是结构破坏倒塌的直接原因.对于即将倒塌或可能经历后续地震的结构，残余变形会对其产生严重影响［3］，同时，当残余变形角大于0.5%时，建筑的维修成本便大于重建成本［4］.为了减少或者消除防屈曲支撑体系的残余变形，根据基于影响的抗震设计概念，满足一些业主或者投资者提出的更高要求，Ricles等［5］提出自复位后张钢框架体系的概念并进行了研究.此后，国内外学者展开了针对自复位体系的相关研究.Tremblay等［6］对自复位摩擦型耗能支撑铰接框架和防屈曲支撑框架的分析表明:小震时，前者层残余变形与层高比最大仅为0.08%，而后者则达到 1.51%;中震时分别为0.23%，2.79%;大震时分别为1.07%和3.83%.Karavasilis等［7］分析了装有自复位黏滞阻尼器的钢框架结构的地震反应，验证了该种阻尼器可减小结构及非结构构件的反应.宋子文［8］也对装有自复位支撑及防屈曲支撑的6层刚接钢框架分别进行了时程反应分析，结果显示:在罕遇地震作用下，前者的最大位移仅为后者的30%，后者残余变形角为0.5%，而前者几乎为零.此外，潘振华等［9］对安装有不同形式自复位阻尼器的框架进行分析，证明了这类阻尼器在减少地震反应及残余变形方面的功效.

国外现有的自复位支撑构件耗能形式部分为摩擦耗能［10］，虽然其曲线较为饱满，但是存在螺栓松动及摩擦面疲劳老化的突出问题.

针对以上问题，本文提出了一种新型防屈曲支撑——自复位防屈曲支撑，阐述了此类支撑的构造方式及力学原理，并对其进行了拟静力试验研究，以探索其滞回性能及复位效果.

1 自复位体系的构造及工作原理

自复位防屈曲支撑由2个部分组成:防屈曲支撑(BRB)和自复位(SC)系统.

1.1 防屈曲支撑的组成

防屈曲支撑由约束套管(外套管和内套管各1个)、2个耗能内芯(EDC)及一些连接部件组成.外套管与内套管等长并且同心.一个耗能内芯夹在内、外套管的上表面之间，另一个夹在内、外套管的下表面之间.耗能内芯一端与内套管相连，另一端则与外套管相连.内、外套管除了充当耗能内芯的约束套筒，还应为耗能内芯传递外荷载.为了实现以上目的，在组装时，2个耗能内芯左端分别与内套管上、下表面焊接，然后整体滑入外套管，并将2个耗能内芯的右端与外套管上下表面的槽2焊接(见图1(a)).从图1(a)中的剖面1-1，2-2及3-3中可看出内套管、外套管及耗能内芯三者在支撑两端及中部的位置关系及连接方式.根据不同的结点形式或者试验需要，支撑两端各需要一个连接系统以传递外荷载.左连接系统为左T形连接板，右连接系统由右矩形连接板、右连接角钢、右T形连接板及高强螺栓组成.整个防屈曲支撑系统的运动机理为内套管和外套管之间的相对运动拉动或推动与它们相连的耗能内芯伸长或缩短.耗能内芯(EDC)恢复力模型可简化为一个双线性弹塑性模型，如图1(b)所示.图中，纵坐标为作用在耗能内芯的轴向荷载Fc;横坐标为耗能内芯的变形量uc;Fyc为耗能内芯的屈服力;uyc为屈服变形;Fcm为耗能内芯的最大恢复力;ucm为耗能内芯的最大位移;Foc为耗能内芯回到位移零点时的恢复力(即残余力);Kc1为耗能内芯的弹性刚度;Kc2为耗能内芯的屈服后刚度.

图1 防屈曲支撑系统

1.2 自复位系统的组成

自复位系统是在防屈曲支撑的基础上增加了预应力复位材料，使得体系在初始阶段便有很大的抵抗变形的刚度储备.复位筋按照图2(a)的方式锚固于左右2块端板上.2块端板分别位于外套管(也即内套管)的两侧，与2个套管间仅有接触压力，无其他连接.从图2(a)中的剖面1-1可看出主要部件内套管、外套管、耗能内芯及复位筋四者的位置关系.不考虑耗能内芯的作用时，复位系统的恢复力为双线性弹性模型，如图2(b)所示.图中，纵坐标为作用在整个支撑上的轴向荷载Fs;横坐标为复位筋的变形量us;Fys为自复位系统的“屈服力”;uys为“屈服位移”.外荷载为零时，刚性端板将复位筋中的预应力F0按刚度分配给内、外套管，其反力分别为Fin和Fout.此时，内、外套管压缩位移为 uys=F0/Ks1=Fys/Ks1，其中，Ks1=Kb+Kout+Kin，Kb，Kout，Kin分别为复位筋、外套管及内套管的刚度.当外力F增大时，2个套管的压缩量减少，复位筋伸长;直到外力F≈F0，2个套管恢复原长.在这个过程中，套管和复位筋一直处于变形协调的状态，总刚度为整个过程中最大，对应图2(b)中的第一刚度Ks1.此后，内、外套管开始相对运动，自复位体系的总刚度为Ks2=Kb.由于连接端的刚度影响仅相当于在整个系统上串联2个已知刚度的弹簧，因此在分析体系力学机理时，先不作考虑.

图2 自复位系统组装与恢复力模型

自复位防屈曲支撑系统实际工作时，耗能内芯及自复位体系可视为并联受力，独立工作.因此，系统的总滞回模型可由两者的恢复力叠加得到，如图3所示.图中，纵坐标Fsc为自复位防屈曲支撑的恢复力;横坐标us为复位筋的变形量;Fy为自复位防屈曲支撑在位移为uys时的“恢复力”;Fm及um分别为自复位防屈曲支撑的最大恢复力和最大变形.体系总恢复力可表示为

图4为自复位系统的力学原理图.

图3 自复位防屈曲支撑理论滞回模型

图4 自复位防屈曲支撑力学原理

1.3 复位系统与防屈曲支撑的关系

由图1(b)和图2(b)可知，当防屈曲支撑与自复位体系都回到位移零点时，自复位体系的恢复力为零，防屈曲支撑的恢复力为 Foc≤Fcmax，其中Fcmax为考虑耗能内芯强化后的最大恢复力.显然，在位移零点时，Foc与Fys并不平衡.但若使 Fys≥Fcmax，便能保证复位系统与防屈曲支撑平衡时的位移小于uys=Fys/Ks1.对于一般自复位防屈支撑构件，由于Ks1包含了2个钢管的弹性刚度，其相对于预应力F0=Fys来说很大，即uys很小，因此当两者平衡时的残余位移可忽略不计，可视其已达到复位效果.由于Fys=F0，因此F0≥Fcmax即为保证自复位防屈支撑复位的条件.

由于自复位防屈曲支撑的耗能能力完全取决于其中的耗能内芯，因此在保证复位的前提下，增大耗能内芯的弹性刚度及屈服位移便能增大耗能能力，而预应力则越小越有利于耗能.因此，F0=Fcmax为复位筋与耗能内芯之间的最优配置.

2 自复位防屈曲支撑试件的设计与制作

2.1 耗能内芯的材性试验

耗能内芯板性能如表1所示，延伸率达35%，可看出此批钢板具有良好的延性，适合作为耗能材料.

表1 耗能内芯材料性能试验结果

2.2 自复位防屈支撑试件预应力F0的设计及自复位材料的选取

根据内芯材料性能试验结果及防屈曲支撑试验结果［1］，可预测 Fcmax=1.5Fyc=129 kN，取 F0=1.5Fcmax=2.25Fyc≈200 kN.

理想的自复位材料不仅要提供恢复力，还应具备足够的可恢复变形能力.例如，按照大震时使框架层位移达到2%，则支撑的变形应达到0.87%.本设计中支撑总长为1 950 mm，其中复位筋复位段长度约为1 100 mm.假设支撑与水平成30°角，不考虑支撑与结构连接节点的影响，那么复位段在加载过程中的伸长率需求则为1.54%.

设自复位材料总应变为δdb，则

式中，δb0为预应力阶段复位筋的变形率，δb0=F0/(EbAb)=0.18%，Eb，Ab为复位筋弹性模量和截面积;δ为复位筋在试件加载过程中的伸长率.

根据以上计算，为了使内芯充分耗能，自复位防屈曲支撑的变形应达到δdb=1.72%，远远超过正常钢材的弹性变形极限(0.1% ～0.9%).分别对玻璃纤维绳(GROPE)、高强度钢绞线、玻璃纤维增强树脂棒材(GFRP)以及杜邦公司生产的Kelvlar芳纶纤维增强树脂棒材(AFRP)进行了拉伸试验，结果见表2.由表可见:玻璃纤维绳虽然变形能力尚可，但其强度过低，这样会导致其截面过大，不适合实际应用;玻璃纤维增强树脂筋虽然强度很高，变形能力也较强，但是在远小于其理论强度时出现了滑移，因此尚需要对其锚固进行系统的研究;AFRP棒材强度很高，但变形能力不足.而高强度钢绞线的强度满足要求，并且锚固也相对简单，因此，本试验采用1 860 MPa高强度钢绞线提供复位力.

表2 4种拉伸材料的材料性能试验结果

2.3 自复位防屈支撑试件主要零部件设计及加工

根据以上设计准则，共设计了4个试件.表3给出了试件编号和试件类型，其中BRB，SC，SCBRB分别表示防屈曲支撑、纯复位装置及自复位防屈曲支撑.试件主要组成部件尺寸及材料如表4所示，部分零件如图5所示.

表3 试件编号

图5 自复位防屈曲支撑的部分零件

表4 自复位防屈支撑试件主要零部件尺寸及材料

3 自复位防屈曲支撑的拟静力试验

为了便于对比复位效果，分别进行防屈曲支撑(B-1)、复位装置(B-2，B-3)及自复位防屈曲支撑(B-4)共4个试件的拟静力试验研究.试验在哈尔滨工业大学结构与抗震实验中心的2 500 kN MTS TestStarⅡ型电液伺服试验机上进行.

3.1 防屈曲支撑B-1的拟静力试验

图6为防屈曲支撑B-1试验照片.该试验以位移控制加载，采用锯齿波，加载速率为4 μm/s.加载结果如图7所示，可看出B-1虽然具有良好的耗能效果，但是却存在明显的残余变形，表5给出了各圈中残余变形与最大变形.由表中数据知，两者比值从第1圈的0.68增大到第4圈的0.87.可见，随着最大变形的增大，其残余变形也显著增加.

图6 B-1拟静力试验装置图

图7 B-1的滞回曲线

表5 B-1最大变形与残余变形

3.2 纯复位装置B-2和B-3的拟静力试验

为了验证预应力是否达到预期值，对纯复位支撑B-2和B-3进行拟静力试验.试件B-2试验按照力控制加载，加载速率为3 kN/s，加载至±590 kN，往复4圈.试验得到的复位装置力-位移曲线如图8所示.但在接近位移零点范围内(约±1 mm内)，试验的刚度几乎为零，没有出现理想的双折线.经推断，可能是以下原因:①焊接外套管与右连接系统时，高温使得原本施加的预应力几乎消失;②2个钢管之间可能存在着2 mm的长度差，使得较短的钢管在较长的钢管内部自由滑动了2 mm.

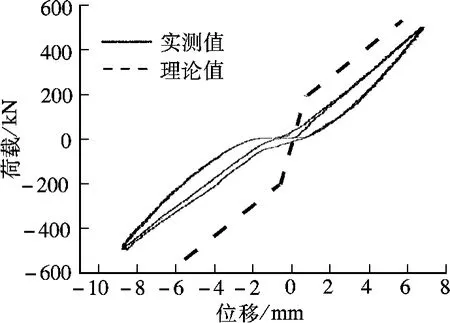
图8 B-2的力-位移曲线

为此，试件B-3的右连接系统用螺栓连接代替焊接，以消除焊接对张拉完的预应力的影响，试件照片如图9所示.对B-3进行拟静力试验，得到的结果曲线如图10所示.可看出试件产生很大滑移并出现了滞回，这是由于给高强螺栓施加的扭矩不足.但值得注意的是，在接近位移零点位置附近的零刚度段被消除，这说明预应力已经加上，因此试件B-2的失败可以排除是由于2个钢管可能不等长所致.

图9 螺栓组装试件B-3

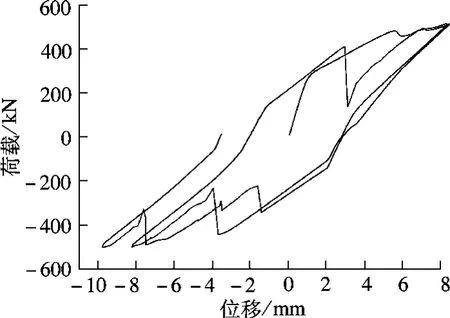
图10 B-3的力-位移曲线

因此可以判断试件B-2失败的原因应为后续的大量焊接极大削弱了其本身已经建立的预应力，甚至可以使预应力完全消失.

给螺栓施加更多的预紧力后再进行试验，结果见图11.可看出，试件出现了双折线形的力-位移曲线，说明预应力已经加上.按照设计的张拉控制，总预应力应为200 kN，而实际预应力仅为110 kN，相当于1.3倍内芯初始屈服力.这是由于用油表来标定预应力仍然存在较大的误差.从图11还可看出，试验存在0.31 mm的残余变形，这是由内、外套管之间的摩擦引起的.

图11 增大螺栓扭矩系数后B-3的力-位移曲线

3.3 自复位防屈曲支撑试验

自复位防屈曲支撑B-4的试验采用与B-3相同的加载速率，得到图12中的滞回曲线.可看出B-4具有良好的复位效果，但是存在0.52 mm的残余变形.此变形应减去B-3的残余变形(0.31 mm)才能视为由耗能内芯的存在产生的残余变形.因此实际残余变形仅为0.21 mm，与最大变形比值为4.5%，占试件总长的0.011%，此变形小于1.3节提及的uys，表明复位效果理想.

图12 B-4的力-位移曲线

4 结论

1)自复位防屈曲支撑综合了自复位体系及防屈曲支撑的优点，构造合理，力学原理明确，以普通钢材及钢绞线为原材料，具有良好的工程应用前景.

2)预应力的成功施加及可靠的锚固是保证该构件复位性能的重要环节.预应力等于耗能内芯整个工作过程中的回复力时，耗能与复位功能达到最优配置.本试件中，预应力达到1.3倍内芯初始屈服力时，可提供足够的恢复力.当预应力施加完成后，不宜对构件进行焊接、热切割等操作，因为过大的热量会严重削弱预应力，甚至使其消失.

3)经过合理设计和加工，自复位防屈曲支撑能够克服防屈曲支撑耗能内芯的残余变形，达到预期复位效果.

References)

［1］Zhao J X，Wu B，Ou J P.Flexural demand on pin-connected buckling-restrained braces and design recommendations［J］.Journal of Structural Engineering，ASCE，to appear.

［2］贾明明，张素梅.采用抑制屈曲支撑的钢框架结构性能分析［J］.东南大学学报:自然科学版，2007，37(6):1041-1047.Jia Mingming，Zhang Sumei.Analysis of steel frame installed with buckling-restrained braces［J］.Journal of Southeast University:Natural Science Edition，2007，37(6):1041-1047.(in Chinese)

［3］Christopoulos C，Pampanin S，Priestley M J N.Performance-based seismic response of frame structures including residual deformations.PartⅠ:single-degree of freedom systems［J］.Journal of Earthquake Engineering，2003，7(1):97-118.

［4］Erochko1 J，Christopoulos C.Residual drift response of SMRFs and BRB frames in steel buildings designed according to ASCE 7-05［J］.Journal of Structural Engineering，ASCE，2011，137(5):589-599.

［5］Ricles J M，Sause R，Garlock M，et al.Posttensioned seismic-resistant connections for steel frames［J］.Structural Engineering，2001，127(2):113-121.

［6］Tremblay R，Lacerte M，Christopoulos C.Seismic response of multi-storey buildings with self-centering energy dissipative steel braces［J］.Struct Eng，2008，134(1):108-120.

［7］Karavasilis T L，Martin T B，Williams S.Development of nonlinear analytical model and seismic analyses of a steel frame with self-centering devices and viscoelastic dampers［J］.Computers and Structures，2011，89(11/12):1232-1240.

［8］宋子文.自复位耗能支撑结构的地震响应分析［D］.哈尔滨:哈尔滨工业大学土木工程学院，2010.

［9］潘振华，潘鹏，叶列平，等.自复位钢框架节点有限元模拟及参数分析［J］.建筑结构学报，2011，32(3):35-42.Pan Zhenhua，Pan Peng，Ye Lieping，el al.Modeling and parametric study of beam-to-column connection for selfcentering steel moment frames［J］.Journal of Building Structures，2011，32(3):35-42.(in Chinese)

［10］Christopoulos C，Tremblay R，Kim H-J，et al.Selfcentering energy dissipative bracing system for the seismic resistance of structures:development and validation［J］.Structural Engineering，2008，134(1):96-107.