表贴式永磁无刷电机直接解析计算方法

李节宝 井立兵 周晓燕 章跃进

（上海大学机电工程与自动化学院 上海 200072）

1 引言

永磁电机气隙磁场分析是电机设计和性能计算的基础。表贴式永磁无刷电机二维气隙磁场可以采用数值法或解析法求解。有限元法适应性强、计算精度高，但建模和计算时间较长，在电机的优化设计中并不方便。解析法物理概念清晰，解析函数式较直观地反映各参数与磁场分布的关系，参数调整方便，计算量小、速度快，有利于电机的优化设计和结构调整。

在电机解析模型的分析中，最困难的工作之一就是如何准确计算开槽对气隙磁场的影响。关于解析法用于开槽电机气隙磁场计算的研究已有大量的文献。文献[1,2]较早提出在极坐标系下采用标量磁位法计算表贴式径向充磁永磁无刷电机的气隙磁场。首先计算未开槽时电机气隙磁场，然后利用保角变换求得电枢开槽时的气隙相对磁导函数，并与无槽时的气隙磁场相乘，从而得到计及开槽效应的二维气隙磁场。该方法存在槽口切向磁场分量被隐没的问题，影响麦克斯韦应力张量法计算电磁转矩的精度；文献[3]引入复数相对磁导函数，克服了切向气隙磁通密度分量被隐没的缺点。但非线性复磁导函数求解过程复杂、计算时间长。以上方法均采用无限深单槽模型，不考虑槽与槽之间的影响，且无法知道槽内磁场情况，不利于绕组感应电动势的精确计算。文献[4]将求解区域划分为气隙区域和槽形子区域，利用两区域重叠部分的计算结果作为另一区域的边界条件，从而计算出开槽时的气隙磁场。两区域磁场交替计算，经若干次迭代得到满足精度的结果。该方法考虑了实际槽形分布，计算结果更符合实际，但槽形种类多，难以获得统一的解析模型。文献[5,6]分别将标量磁位解析法、矢量磁位解析法与差分法相结合计算表贴式永磁无刷电机磁场，文献[7]将解析法和等参元法结合计算分数槽永磁无刷电机的气隙磁场。解析法与数值法结合能精确地处理各种复杂槽型，计算速度快于数值法，但计算过程中需要反复迭代，因此计算时间仍较长，且计算精度要受到迭代精度影响。

文献[8]建立了外转子表贴式永磁无刷电机直接解析法模型，并以一台简化的四极电机为例计算了其空载气隙磁通密度和齿槽转矩。本文根据文献[8]的基本思路，建立了内转子永磁无刷电机直接解析模型。直接解析法形成的整体系数矩阵十分庞大，为了减少一次求解的计算量，本文采用槽内磁场与气隙磁场分步求解的方法，有效降低了系数矩阵维数，并利用周期性条件减少计算量。

根据表贴式内转子径向充磁永磁无刷电机模型结构特点，将解析模型划分为三个子区域，即气隙、永磁体和槽区域，分别建立了各区域矢量磁位拉普拉斯方程或泊松方程，并由交界条件连接各子区域方程式，采用直接解析法求得空载气隙磁场和槽内磁场解析表达式。通过对一台44极48槽内转子表贴式径向充磁永磁无刷电机实际样机计算及计算结果的比较，验证了本文模型推导的正确性和该方法的有效性。计算速度相较有限元法和解析数值结合法有明显提高。

2 直接解析法空载磁场计算基本原理

表贴式永磁无刷电机（以内转子电机为例）定子铁心内表面开槽后，不仅对气隙主磁场分布产生影响，且相邻槽之间也会有影响。为了便于分析，作如下假设：

（1）计算场域为二维磁场，忽略端部效应。

（2）定、转子铁心磁导率无穷大。

（3）永磁体径向充磁且相对磁导率μr=1。

（4）定子槽为径向直槽，空载槽内无电流。

根据电机物理结构和材料属性，整个求解区域划分为三部分：气隙区域 I、永磁体区域 II和槽区域 Si(i=1,2,3,…Q)，二维极坐标系下电机物理模型及求解区域划分如图1所示。

图1 表贴式永磁无刷电机求解模型Fig.1 Model of a surface-mounted PM motor

图1a中Rr为转子铁心外半径，Rm为永磁体外半径，Rs为定子内半径，Rsy为计及槽深后槽底与转子中心的距离，β 为槽口宽度（以下计算中转换为弧度），θi为第i槽距离初始设定基准位置间的角度，模型建立初始时刻磁极S极正对槽中心线处，因此，θi=-β/ 2+2iπ/Q，Q为槽数。

2.1 气隙和永磁体区域矢量磁位数学模型

永磁体径向充磁，在二维极坐标系下只有z轴分量有效，由傅里叶分解得其磁化强度M表达式为r和θ 的函数[1]

式中 v——永磁体磁场计算谐波次数；

p——极对数；

θ0——永磁体与初始设定的基准位置间偏移角度，本文模型中为0；

αp——极弧系数。

在极坐标下气隙区域I和永磁体区域II矢量磁位方程式为如下：

气隙区域I拉普拉斯方程

由分离变量法得以上区域通解表达式如下[9]

式中，m为槽数Q和极对数p的最大公约数。

极坐标系中，磁感应强度与矢量磁位有如式（6）的关系

因此，结合式（6），由图1电机物理模型和材料属性可得如下气隙和永磁体区域的边界条件

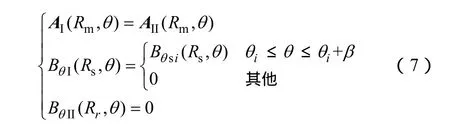
2.2 槽区域矢量磁位数学模型

由于采用了直槽模型，简化了槽区域边界条件，便于其矢量磁位拉普拉斯方程的求解。空载时二维极坐标系下第i槽的矢量磁位拉普拉斯方程为

由分离变量法得槽区域通解[8]

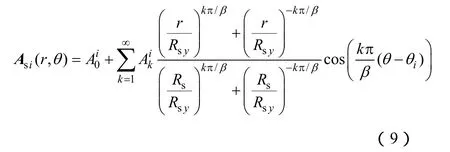
式中 k——槽区域磁场谐波次数，k=1,2,3,…。

由于槽口处磁位连续，可利用槽口处气隙区域矢量磁位傅里叶分解求得槽区域矢量磁位常数和各次谐波次数系数表达式，如下式

由式（4）、式（5）、式（12）及边界条件式（7）和式（14），可解得气隙和永磁体区域区域矢量磁位系数 AIn、BIn、CIn、DIn和 AIIn、BIIn、CIIn、DIIn表达式（见附录A.1）。又由式（10）和式（11）可知，在得到气隙区域矢量磁位 AI(r,θ)后即可解得槽区域矢量磁位系数（见附录A.2），由此便能求解出槽区域的磁场分布。

3 齿槽转矩和空载反电动势计算

齿槽转矩和空载反电动势是对电机负载运行性能有重要影响的两个量，其准确计算对于电机设计和性能分析十分重要。在获得空载气隙磁场和槽区域磁场分布后，即可较方便地计算出这两个参数。

3.1 齿槽转矩计算

齿槽转矩由定子开槽引起，与定子电流无关。计算电机的齿槽转矩主要有两种方法：虚位移法和麦克斯韦应力张量法。虚位移法的缺点是计算繁复且效率较低，而麦克斯韦应力张量法计算转矩只需要在气隙内部沿圆周进行一次线积分，理论上计算结果与积分路径无关，结合本文直接解析法特点，选用麦克斯韦应力张量法计算齿槽转矩，由式（4）和式（6）可得齿槽转矩计算表达式为

由式（15）可以看出，只要求出气隙区域 I矢量磁位 AI(r,θ)表达式系数即可较方便地求得齿槽转矩。

3.2 感应电动势计算

空载反电动势计算常用的方法有磁链分解法、磁位分解法和磁链微分法。由于磁链分解法和磁位分解法只能计算出某一固定时刻的值，而不能求出动态的随时间变化的空载反电动势波形，因此本文计算中采用磁链微分法

式中 ω——机械角速度。

假设绕组线圈在槽内均匀分布，则单个槽内磁链计算可由该槽内矢量磁位积分获得, 由于每槽为双层绕组，故每个绕组的磁链表达式为

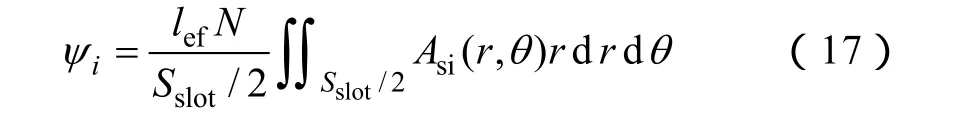
通过计算转子在不同时刻的绕组磁链，即可获得转子位置角函数的相绕组磁链波形，从而可以很方便地求得转子在任意速度旋转时相绕组反电动势。

4 解析计算结果分析比较

为了验证本解析计算方法的有效性，本文利用以上解析计算模型，对一台44极48槽内转子结构永磁无刷电机空载气隙磁场、齿槽转矩和反电动势进行计算，计算结果同二维有限元计算程序计算结果及实验波形作比较。电机基本数据为定子内径90mm，单边气隙长度 0.8mm，槽口宽 1.6mm，槽深 22.5mm，绕组匝数 50，铁心轴向长度 50mm，永磁体厚度8mm，极弧系数ap=0.9，剩磁Br=1.25 T。计算中气隙区域磁场谐波次数n取 275，槽区域磁场谐波次数k取200。计算结果及比较如图2所示。

图2a和2b为空载气隙磁场径向磁通密度和切向磁通密度波形，图中分别标识了直接解析法计算结果和有限元法计算结果以作比较。

图2 空载气隙磁通密度波形比较Fig.2 The comparison of flux density waveform in the middle of the air-gap

由图2波形比较分析可知，图中径向磁通密度曲线的下凹对应定子槽引起的磁通密度的下降；由于齿边缘区域的气隙磁导急剧变化引起聚磁效应，使得径向和切向气隙磁通密度计算结果图形在齿边缘出现一个磁通密度尖峰。从图中可看到直接解析法计算相对有限元计算结果在齿边缘的聚磁效应要稍微偏弱，但整个波形均吻合较好，可见本解析计算方法是准确有效的。

图3为直接解析法和有限元法计算的齿槽转矩一个周期变化波形比较。理论上齿槽转矩的最低次谐波是极数p和槽数Q最小公倍数，因而理论周期为(22×360°)/(11×12×4)=15°，从图中可看到齿槽转矩为周期 15°电角度的脉动转矩。比较图中可以看出采用麦克斯韦应力张量法计算所得的齿槽转矩与有限元法计算结果相对吻合。

图3 齿槽转矩波形比较Fig.3 The comparison of cogging torque

图4 相绕组空载反电动势波形比较Fig.4 The comparison of no-load EMF waveforms in a phase winding

图4a为永磁无刷电机在转速 140r/min时电机相绕组空载反电动势直接解析法计算波形，峰值100V。图 4b为样机实验波形，横轴为时间轴，每大格为10ms，共计0.1s，纵轴为反电动势幅值，每大格为50V，正负均为100V。由图4a和4b比较可知解析计算反电动势无论是时间周期还是波形幅值均较为一致。充分肯定了本直接解析法的计算精度。

5 结论

本文建立了表贴式径向充磁永磁无刷电机空载矢量磁位磁场解析模型，编写了相应的解析计算程序，以实际样机为例计算了其空载气隙主磁场、齿槽转矩和反电动势，与有限元法计算结果和实验波形相比较证明了本方法的正确性和有效性。该方法既保证了计算结果的准确性，又可很方便地获得气隙磁场和槽内磁场的解析解，为进一步研究与气隙磁场和槽内磁场有关的物理量提供了方便。本文采用的矢量磁位解析法计算速度较快，不仅适合分数槽电机，同样适合整数槽电机，具有普适性。

附 录

1.气隙区域I和永磁体区域II矢量磁位

表达式系数如下：

表达式为

[1]Zhu Z Q, Howe D, Bolte E.Instantaneous magnetic field distribution in brushless permanent magnet DC motors, part I: open-circuit field[J].IEEE Transactions on Magnetics, 1993, 29(1): 124-135.

[2]Zhu Z Q, Howe D.Instantaneous magnetic field distribution in brushless magnet DC motors, part III effect of stator slotting[J].IEEE Transactions on Magnetics, 1993, 29(1): 143-151.

[3]Damir Zarko, Drago Ban, Thomas A Lipo.Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J].IEEE Transactions on Magnetics, 2006, 42(7): 1828-1837.

[4]Zhilichev Y.Analysis of permanent magnet machines using crossing macro-elements[J].IEEE Transactions on Magnetics, 2000, 36(5): 3122-3124.

[5]丁晔, 章跃进.表面磁钢永磁无刷电机空载气隙磁场半解析法研究[J].电机与控制应用, 2007(3): 7-10.Ding Ye, Zhang Yuejin.Semi-analytical method research for non-load air gap field of surface alnico permanent magnet brushless motor[J].Electric Machine and Control Application, 2007(3): 7-10.

[6]郑成勇, 章跃进, 薛波, 等.表贴式分数槽电机永磁气隙磁场矢量位半解析法[J].微特电机, 2010(4):24-26.Zheng Chengyong, Zhang Yuejin, Xue Bo, et al.Semi-analytical approach with vector magnetic potential for permanet-magnet air-gap field of surface mounted stator slot[J].Small and Special Electrical Machines,2010(4): 24-26.

[7]李春江, 章跃进, 卢铁斌, 等.解析数值结合法在直驱轮毂式永磁无刷电机气隙磁场分析中的应用[J].微电机, 2010, 43(12): 21-28.Li Chunjiang, Zhang Yuejin, Lu Tiebin, et al.Application of analytical-numerical method to air-gap magnetic field of direct drive wheel-hub permanent magnet brushless motors[J].Micromotors, 2010,43(12): 21-28.

[8]Thierry Lubin, Smail Mezani, Abderrezak Rezzoug.Exact analytical method for magnetic field computation in the air gap of cylindrical electrical machines considering slotting effects[J].IEEE Transactions on Magnetics, 2010, 46(4): 1092-1099.

[9]胡之光.电机电磁场的分析与计算[M].北京: 机械工业出版社, 1986.