基于PR调节器的PWM整流器VFOC控制

戴鹏，董苏，程尧，符晓

（中国矿业大学 信息与电气工程学院，江苏 徐州 221008）

1 引言

三相电压源型PWM整流器（VSR）可以实现网侧电流正弦化、单位功率因数运行以及能量双向流动等功能，在高性能变流系统中获得广泛应用［1］。常用的电压定向控制（VOC），由于采用的传感器较多，增加系统成本的同时带来相应的检测误差和复杂性。虚拟磁链定向控制（VFOC），省去电网电压传感器，通过估计虚拟磁链间接获得坐标变换中所需要的电网电压角度信息［2］。

传统VFOC控制策略基于两相旋转坐标系下的三相VSR数学模型，因模型中含有交叉耦合项，需要前馈解耦控制，使整个控制系统的结构变得复杂。为避免上述缺点，本文研究了两相静止坐标系下的VFOC控制策略，电流控制采用比例谐振（PR）调节器取代传统的PI调节器。PR调节器能够将输入信号幅值放大，而不改变给定信号的相位和频率，实现交流量在两相静止坐标系下的稳态无静差控制［3］，简化了控制系统的设计。仿真和实验结果证明了该方法的可行性。

2 两相静止坐标系下的VFOC控制策略

2.1 两相静止坐标系下三相VSR的数学模型

三相VSR的主电路拓扑结构如图1所示。其中，ea，eb，ec为三相电网电压，L，R 为进线电抗器的电感和电阻，Udc为直流母线电压。

图1 三相VSR的主电路拓扑结构Fig.1 Main circuit topology of three－phase VSR

忽略进线电抗器和线路的电阻R，则在α－β坐标系下PWM整流器的电压方程为

式中：Sa，Sb，Sc为三相桥臂的开关函数，为1时表示桥臂上管开通，下管关断，为0表示桥臂下管开通，上管关断；eα，eβ，iα，iβ分别为电网电压和电流的α，β分量。

对式（1）两边同时积分，可得：

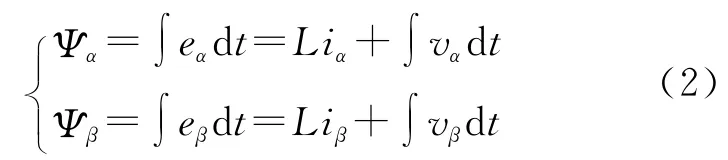
根据式（2）可计算出虚拟磁链角度为

由上述分析可知，电网电压虚拟磁链角度可以通过逆变电压以及输入电流计算得到，而无需检测电网电压。

2.2 虚拟磁链观测器

磁链计算式（2）中含有积分项，实际观测中纯积分环节会造成积分饱和以及直流偏移等问题，影响观测精度。本文在采用一阶低通滤波器代替纯积分器的基础上，引入补偿环节对低通滤波器的输入进行相位和幅值补偿，改善传统积分器观测精度。

电压与磁链的频域关系为Ψ＝u／（jωe），采用低通滤波器代替纯积分，则有：

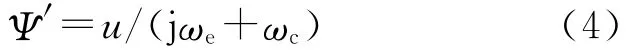
式中：ωc为低通滤波器的截止频率；ωe为电网角频率。

低通滤波器与纯积分环节的幅值和相位的关系可表示为［4］

设Z为补偿函数，则

当采用新型的积分器引入补偿环节对低通滤波器的输入进行补偿，则：

由此得到新型改进积分器的补偿算法：

图2为磁链观测器的原理图。

图2 磁链观测器原理图Fig.2 Schematic of flux observer

3 基于PR的VFOC控制算法

传统的PI控制器只能无差跟踪直流给定信号，在两相静止坐标系下，被控对象是交流量，采用PR调节器能够对交流信号实现稳态无静差控制，而且易于数字化［5］。其传递函数为

其中，比例系数KP决定控制器的带宽和稳定程度。积分系数KR决定谐振频率附近的带宽。

考虑系统的动态性能，由于采样和计算以及PWM产生过程中的延时性，控制量与输出信号iα，iβ之间存在一定的延迟，由于α轴和β轴完全对称，只对α轴分析，那么可得

利用位移原理，对式（10）进行Laplace变换：

利用泰勒公式将式（11）展开，根据近似处理条件［6］得：进而可得：

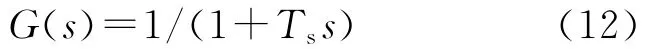
使用一个P调节器K，即可完成对输出电流的控制，但是在两相静止坐标系中的电流是交流量，需要使用PR调节器代替传统PI调节器才能实现交流电流跟踪。使用PR调节器对电流控制，根据式（1）得到vα，vβ的控制方程：

综上所述，图3给出了基于PR调节器的VFOC控制结构框图。与采用电压定向的电压、电流闭环控制相比，电流环使用PR调节器代替PI调节器，在两相静止坐标系下没有交叉耦合项，简化整个控制系统。另外，采用VFOC控制策略，省去了网侧电压传感器，旋转坐标变换中的角度信息通过磁链观测器得到，降低系统成本的同时进一步简化了系统控制结构。

图3 基于PR调节器的VFOC控制结构框图Fig.3 Control block diagram of VFOC based on PR

4 控制系统仿真分析

为验证该方法的有效性和可行性，文中基于Matlab软件进行了仿真研究。参数如下：电网电压有效值为220V，直流母线电压Udc＝600V，等效电感L＝10mH，等效电阻R＝1Ω，C＝3300 μF，负载电阻RL＝100Ω，在0.5s时刻负载电阻由100Ω突变为50Ω。

图4a、图4b分别给出了整流和逆变两种情况下A相电压、电流（放大5倍）的仿真波形，由图4a、图4b可知，这两种情况下VSR可实现单位功率因数运行；图4c为0.5s时刻，负载从100 Ω突变为50Ω时输入电流仿真波形，具有较好的动态跟踪性能；图4d给出了直流母线电压波形，从中可以看出，在启动过程中超调较小，负载突变后能够快速地恢复稳定，系统动态性能良好；图4e为A相电流频谱；图4f给出了磁链观测器观测的角度值与实际电网电压角度，由图可知，在负载变化时磁链观测器的观测结果没有产生明显波动。

图4 控制系统仿真波形Fig.4 Simulation waveforms of control system

5 实验验证及结论

搭建了以PM25RLA120型号的IPM为主电路的实验平台，控制芯片选择TMS320F2812，直流侧电容2200μF，负载电阻100Ω。图5a给出了A相电压电流实测波形，可以看出整流器运行在单位功率因数下；图5b为直流母线电压给定值100V时，负载电阻由100Ω突减至50Ω的A相电流波形和直流母线电压波形，系统具有良好的动态响应性能。

图5 实验波形Fig.5 Experiment waveforms

本文研究了基于两相静止坐标系下的PWM整流器VFOC控制策略，PR调节器代替传统PI积分器，能够实现电流的跟踪控制。与传统的电压定向控制策略相比不仅省去了电网电压传感器，降低系统成本，而且避免了在两相旋转坐标系中的交叉耦合项，不需要前馈解耦，简化了控制系统。仿真和实验结果证明了该方法的有效性和正确性。

［1］Singh B，Singh B N，Chandra A，et al.A Review of Threephase Improved Power Quality AC－DC Converters［J］.IEEE Transactions on Industrial Electronics，2004，51（3）：641－660.

［2］訾振宁，林飞，马颖涛.PWM整流器无电网电压传感器控制策略研究［J］.电气传动，2009，39（10）：27－30.

［3］章玮，王宏胜，任远，等.不对称电网电压条件下三相并网型逆变器的控制［J］.电工技术学报，2010，25（12）：103－110.

［4］刘刚，林都，任一峰，等.异步电机定子磁链观测方法的改进研究［J］.电气传动，2010，40（8）：28－30.

［5］李子欣，李耀华，王平，等.PWM整流器在静止坐标系下的准直接功率控制［J］.中国电机工程学报，2010，30（9）：47－54.

［6］王成智，邹旭东，贾凯，等.滤波器在单相PWM整流器中的应用［J］.高电压技术，2008，34（5）：942－948.