电网电压骤降时PWM整流器的控制
付兴武,张蒙
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125000)
1 引言
电气设备的正常运行是由电网电压的条件决定的。电压的偏差如电压幅度下降、频率的偏差、高次谐波成分等会导致电气设备不正常运行。平衡和不平衡电压骤降会导致系统不稳定和电流形状的严重偏差[1]。干扰的严重程度和设备的电压变化会中断操作或毁坏电气设备。在电力系统中,对电压发生扭曲时有严格的要求。欧洲的标准[2]是允许电压跌落到额定值的10%和有6%的低阶次电压谐波。另外,对可再生能源发电并网的电能质量有严格的要求。可再生能源发电通常都是通过电力电子变换器件连接到电网。电压型PWM整流器在过去几年得到普及。因其双向功率流能力、输出电流为正弦波、直流母线电压恒定和输出滤波电容小[3]等优点被广泛应用到风力发电系统中。但是,连接在电网上的电压型PWM整流器[4]对电网的扰动相当的敏感。尤其是在电压出现瞬间跌落时,交流电流会出现短时间的过流[5],可能会导致系统被迫停机脱网。此外在电压不平衡跌落时,直流电压会出现振荡,这样会影响风力发电机的正常运行。为了提高PWM整流器在电网电压跌落期间的性能,本文对改进的双矢量电流控制器控制策略[6-7]下的PWM 整流器进行了研究分析。此算法是为了消除电压骤降的影响和高次谐波成分。改进的控制算法保证了在电网电压骤降时电流的正弦波形。通过利用Matlab仿真并对仿真结果进行分析,发现双矢量电流控制器控制策略下的PWM整流器在电网电压跌落期间具有良好的性能。
2 电力系统电压骤降
无论输电和配电系统如何良好,许多不同的因素都可导致电压骤降。当今在电力系统中最严重的问题是关于高次谐波和电压骤降。电压骤降是指在电力系统工频电压有效值迅速下降到额定值的10%~90%,持续时间为十几ms到几s。主要有3种原因导致电压骤降:1)电力系统中不同点的短路故障;2)大负载启动;3)非线性负载连接到电网。这些情况发生会导致平衡和非平衡的电压骤降。有4种典型的电压跌落类型[1]如图1所示。

图1 4种典型的电压跌落Fig.1 The four different types of voltage dips
分析电压骤降现象,提出了对称分量理论,三相系统可以表示为3个序列:正序列、负序列和零序列。在三线制系统中零序列现象不会出现,对于平衡系统电压仅有正序分量,非平衡系统的负序分量会加重系统的非平衡。基于空间矢量[8]的方法被用于系统分析。常规的控制策略是对电网电压和网侧电流分别进行采样,并变换到α-β静止坐标系下。简化了计算,并提供了系统的简化模式。
3 电网电压骤降时的交-直流转换器控制
负序成分产生电流干扰并对AC-DC转换器造成大的不平衡。该电网侧的AC-DC变换器在电压扭曲的条件下能正常工作,依赖于所实施的控制算法。这种控制算法在平衡和不平衡电压下降时,必须面对以下问题:线电流失真、直流母线振荡、相位角的变化、电压幅值的变化、电网系统的高次谐波。控制系统的基本假设是平衡的电网电压条件下,但是它对负序列的控制有很大困难。为满足上述问题,本文提出了基于改进的双矢量电流控制器的电压定向控制(VOC)算法。在这种算法中,2个独立的电流控制器工作在正序和负序的同步参照系中(SRF),同时控制电流序列。把三相电流信号变换到与电网电压矢量同步的d-q坐标系下。在同步参照系下,需要一个PI控制器[9]。对称分量理论,是指在稳态下相量的计算,控制算法在瞬时值实施。因此定向电压控制的改进,有必要提取电压和电流的实时序列。在各自的参考坐标系下计算电流控制序列。在静止α-β坐标系下,不平衡电流矢量由2个部分组成:

转换到同步参照系下的电流分量可以表示为

在正的同步坐标参考系下正序列显示为直流值,负序列显示为100Hz的分量。而在负的同步坐标参考系下正序列显示为一个100Hz的分量,负序列显示为直流值。通过消除这2个频率成分2个电流序列都可以计算出。用低通滤波器测试此方法发现会造成不稳定的问题。最后,为消除双频率成分采用了延迟信号消除(DSC)[10]的方法。DSC是实时序列提取方法,是基于时间延迟同步帧大小的组合。在同步参照系(SRF)中实际信号延迟增加了。这个简单的方法用以消除由直流信号中100Hz的分量,并将其应用于正、负同步坐标参考系下的d轴和q轴电流分量。延迟信号消除的算法描述为

为保证正常工作,输出信号同步,改进VOC的算法必须能够检测到电网电压的相位角。在控制算法中,相角值的有关信息对于信号正确转换是非常重要的。通常,反正切函数应用于电压空间矢量来获取相位角的信息。当电网电压发生扰动,相位角也会产生扭曲,见图2a,导致控制算法失真,不能正常工作。解决的办法是改进锁相环(PLL)算法,工作于d-q同步旋转坐标系下见图2c。锁相环算法的相角估计见图2b。负序分量产生的扰动减小了,产生的相位角是稳定的。
为了加快控制操作和补偿影响,可以加入线电压前馈回路。在实验部分对不同电网电压前馈进行了检查,如静止和同步成分的前馈。由α-β组件前馈得到了最好的控制结果。其方法是通过控制算法,参考信号传输到空间矢量调制器(SVM),在α-β坐标下添加了实际电压信号。前馈减轻了不同的谐波分量的影响,取消不必要的信号改善了整个系统的运行。然而在没有电网电压传感器时不能应用。连接各部分的控制算法:DVCC,PLL,DSC序列提取,电压前馈和改进的VOC控制算法如图3所示。

图2 改进的锁相环算法的优点Fig.2 Advantage of the improved PLL

图3 双矢量电流控制策略Fig.3 Dual vector current control scheme
图4为利用Matlab/Simulink仿真过程中得到的在电压骤降时的电流波形。
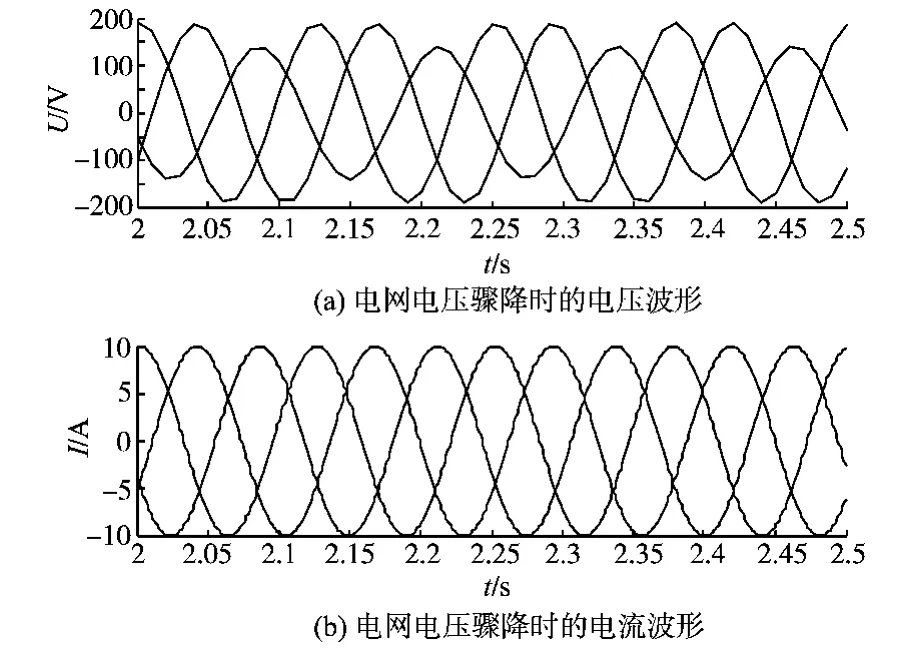
图4 Simulink仿真结果Fig.4 Simulation results by simulink
4 实验结果
改进的空间矢量控制算法用基于dSPACE的PWM变换器进行了实验验证。控制方案如图5所示。主要参数为实验测试额定值:电流10A,电网电压230V,直流母线电压600V,线性滤波电感10mH,开关频率10kHz。

图5 实验控制框图Fig.5 Experimental control block diagram
以下所有的测试在单相电压骤降30%和非正弦电网电压的情况下进行的。在2个同步参照系下提取的电压序列如图6所示。

图6 单相电压跌落时提取的正序和负序电压序列Fig.6 Extracted positive and negative voltage sequence when one phase voltage dip
可以看到,不平衡电压下出现负序现象。在正的同步坐标参考系下参考电流设置为10A。图7显示了改进的电压定向控制算法,在高度扭曲的电压情况下电流保持了正弦形状。传统的电压定向控制方法在控制电流值时没有能力处理出现的负序和振荡的现象,而改进后的算法可以提供稳定的运行。此外,引入了电压前馈能处理更高次的电压谐波。
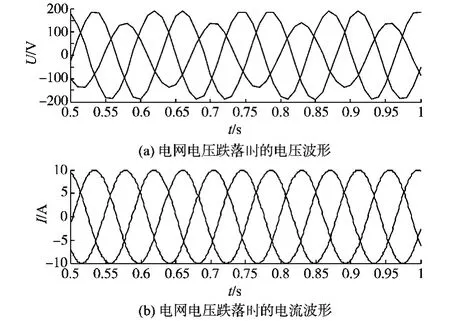
图7 改进的VOC算法,在电网电压跌落情况下电流波形Fig.7 Current shape during voltage dip for improved VOC
5 结论
通过以上的控制策略及实验结果,基于改进的电压定向控制算法交-直流PWM整流器对电压骤降和电网电压谐波失真有良好调节作用。线电压前馈的应用大大提高了正序谐波分量补偿,锁相环(PLL)算法可以得到失真的相位信息。因此,整个系统在电网电压骤降条件下是稳定的。该系统的重要特点是:电网电流仍是正弦;电流序列保持不变。采取了正负序2个控制器,大大提高了控制器的性能,延迟信号消除(DSC)的算法消除了在不平衡电压骤降时100Hz的分量易于用低成本微处理器实现高效的高次谐波补偿。
[1]Bollen M H J.Understanding Power Quality Problems[M].IEEE Press,New Jersey,2000.
[2]EN-50160,Voltage Characteristics of Electricity Supplied by Public Distribution Systems[M].CENELEC,Brussels,1994.
[3]Kazmierkowski M P,Krishnan R,Blaabjerg F.Control in Power Electronics.Selected Problems[M].Academic Press,New York,2002.
[4]张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.
[5]雷乾涛,韩祯祥.电力系统中的电压瞬间跌落[J].华东电力,2003(9):43-48.
[6]Song H,Nam K.Dual Current Control Scheme for PWM Converter Under Unbalanced Input Voltage Conditions[J].IEEE Trans.Industrial Electronics,1999,46(5):953-959.
[7]Roiu D,Bojoi R,Limongi L R,et al.New Stationary Frame Control Scheme for Three Phase PWM Rectifiers Under Unbalanced Voltage Dips Conditions[C]∥IAS 2008.IEEE,2008,1:1-7.
[8]Paap G C.Symmetrical Components in the Time Domain and Their Application to Power Network Calculations[J].IEEE Trans.Power Systems,2000,15(2):522-528.
[9]王长恺,尹华杰.三相电压型PWM整流器的系统设计与PI参数校正[J].电气传动,2011,41(3):41-45.
[10]Aller J M,Bueno A,Paga T.Power Systems Analyzing Using Space-vector Transformation[J].IEEE Trans.Power Systems,2002,17(4):957-965.

