基于FPGA的IHS和提升小波变换的图像融合实现

常亮亮，王广龙，高凤岐，乔中涛，张姗姗

(1.军械工程学院导弹工程系，河北 石家庄 050003;2.上海市计量测试研究院在线通用所，上海 200230)

随着军事侦查、遥感测控领域对图像质量的要求不断提高，人们迫切希望一种能够克服目前各种图像传感器不能按要求提供完整可靠信息的处理方法，图像融合因此成为该领域的研究热点。图像融合是指将多个不同模式的图像传感器所获得的同一场景多幅图像，或同一传感器在不同时刻获得的同一场景的多幅图像，采用一定的算法将各图像数据中所包含的信息优势或互补性有机地结合起来产生新图像的技术［1］。

图像融合方法主要有加权平均法、IHS变换融合法及小波变换融合法等。加权平均法最简单，但效果较差;IHS变换大大提高了融合图像的空间信息表现能力且计算量小，但光谱失真严重;小波变换融合在获得高分辨力的同时较好地保持了图像的原始光谱信息，但在一般的小波变换融合算法中，小波分解的层数对融合结果影响很大，阶数过低或过高都会影响到结果图像的细节表现能力和光谱特性的保持［2］。为了将多种融合算法有机结合，文献［3－4］提出了将小波变换和IHS变换结合的方法，文献［5］提出了采用提升小波技术的图像融合方法。研究普遍认为，小波变换与IHS变换相结合的融合方法能得到比较满意的图像。

目前，小波变换与IHS变换融合算法多采用软件实现，本文提出了一种基于FPGA的IHS变换与提升小波变换相结合的实时图像融合算法，使得算法的运算量极大减少，有效地提高了图像处理的时效性。

1 IHS变换和提升小波变换

1.1 IHS 变换

图像处理中经常应用的彩色坐标系统有RGB模型和IHS模型，两种坐标系统具有各自不同的特点，其中IHS空间中三分量I，H，S具有较强的独立性并能准确定量地描述颜色特征。在图像融合处理中，经常需要建立RGB系统和IHS系统之间的转换关系。通常把图像RGB模型变换到IHS模型称为IHS正变换，而由I，H，S变换为R，G，B称为IHS逆变换。

尽管不同IHS变换法模型在运算速度、复杂度上有所不同，但是变换得到的I，H和S分量图像基本相同。RGB系统与HIS系统的转换公式如下所示。

1)正变换

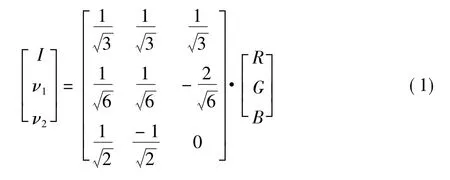
式中:ν1，ν2为中间变量。

2)反变换

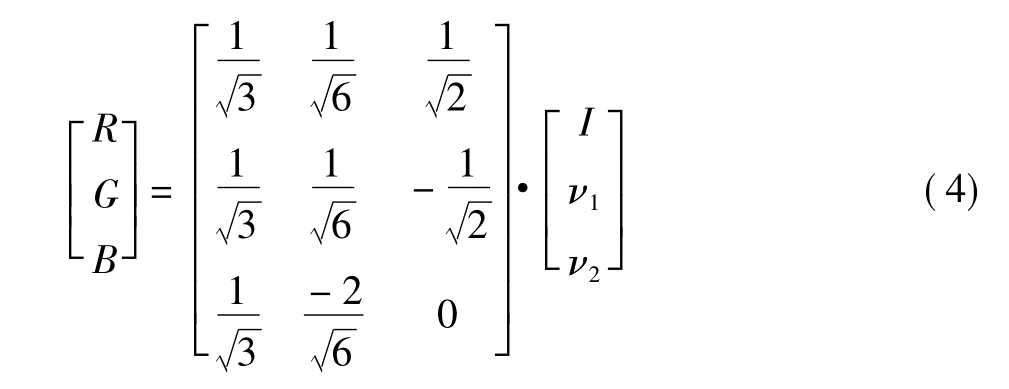
1.2 提升小波变换

提升小波变换是基于提升方案的小波变换，与传统小波变换相比，提升小波算法简单、运算量低、逆变换简单、边界处理容易，因而被广泛应用于图像处理领域。如图1所示，提升方案首先将输入数据分为去相关的偶数序列x(2n)和奇数序列x(2n+1)，然后用偶数序列预测奇数序列得到预测误差d(n)，最后用预测误差来更新偶数序列，得到低频分量c(n)。

图1 提升小波结构框图

2 IHS和小波变换图像融合算法

2.1 算法步骤

IHS和小波变换融合算法的基本思想是将IHS变换法与提升小波变换法结合起来。如图2所示，首先对图像A进行IHS正变换，获得该图像的亮度分量I，H，S;对图像A的亮度分量I和图像B进行提升小波正变换;将图像B小波提升分解后的系数叠加到图像A亮度分量I的分解系数上，而后对亮度分量I进行提升小波逆变换，然后对新的小波系数进行提升反变换以获得新的亮度分量I';将新的亮度分量和第一步IHS正变换得到的H，S进行IHS逆变换以获得融合图像C。

2.2 融合规则

为了便于硬件实现，本文采用的融合规则如式(5)所示，主要是将高分辨力图像小波分解后的系数c2_h与低分辨力图像亮度分量I的c1_h相加后再乘以一个加权系数得到融合图像系数

图2 IHS和小波变换图像融合示意图

3 融合算法的FPGA实现

3.1 IHS变换算法分析及FPGA实现

由RGB系统与IHS系统的转换公式知:在IHS变换中，尽管H，S的求取含有开放和求反正切的非线性运算，但是I，ν1，ν2分量的获得是通过加乘运算实现的。在融合算法中，仅需要I分量及中间量ν1，ν2，并通过新的I'和原 ν1，ν2，进行逆变换可得 R，G，B 值。

本模块是要把RGB格式的图像数据转换成IHS格式的数据，由式(1)可得

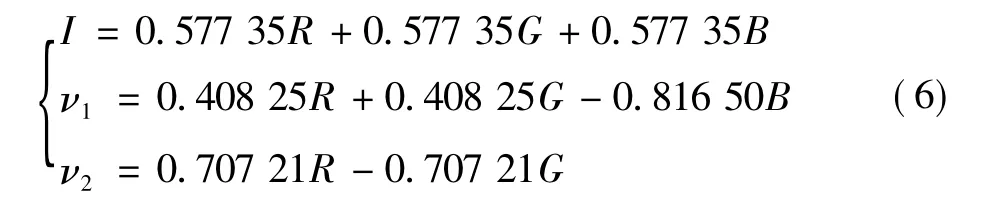
由于上面的计算涉及浮点数乘法，为了便于用Verilog语言在FPGA上实现，需要首先对系数进行放大转换，即

式(7)只涉及整数加乘法，只需将运算结果右移即可得I，ν1，ν2，从而进一步可用 FPGA 实现 IHS变换。仿真结果如图3所示，由图可以看出，对于输入的8 bit RGB信号(159，61，82)，经转换后得到放大的 I，ν1，ν2(174，22，69)，与理论值相同。IHS逆变换的实现与正变换类似。

图3 RGB到IHS变换仿真图(截图)

3.2 小波提升变换的FPGA实现

采用IHS和小波变换相结合的融合方法处理图像时，必须考虑小波分解层数对融合图像质量的影响。研究表明:IHS和小波变换相结合的融合方法明显地改善了影像的质量，融合图像质量对小波分解层数的敏感性较强，在小波分解层数为2，3或4时，都能获得高质量的融合图像［6－7］。本文在二维提升小波变换基础上设计了基于FPGA的多级提升小波变换，以满足图像融合质量和小波分解层数的合理匹配。

3.2.1 一维提升小波正变换的FPGA实现

一维变换的行变换预测为

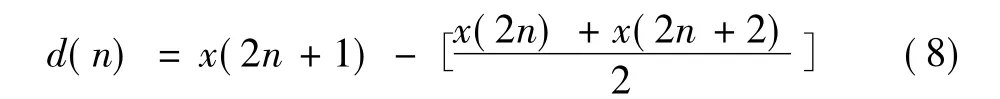
更新运算为

式中:小波基选用可完全重构的5/3提升小波，x(2n)为图像输入数据的偶数序列;x(2n+1)为奇数序列;d(n)为分解后的高频分量;c(n)为分解后的低频分量。

行变换预测的具体实现如图4所示，R1，R2，R3，R4，R5均为寄存器，MUX1，MUX2为多路选择器。由式(1)可知，预测过程中d(n)的值需要x(2n+1)减去相邻2个偶数数据的平均值，所以至少要用3个寄存器，因此，R1，R2，R3被用于寄存当前数据及其左右相邻的数据。MUX1的选择信号在非边界数据时对R1选通，边界数据时对R3选通，用来完成边界数据的对称延拓。由于输入数据是串行逐个输入，故R4寄存器内数据为(x(2n)+x(2n+2))与(x(2n－1)+x(2n+1))，通过多路选择器2，选通(x(2n)+x(2n+2))与R3寄存器运算，运算结果存入R5寄存器，再输出。

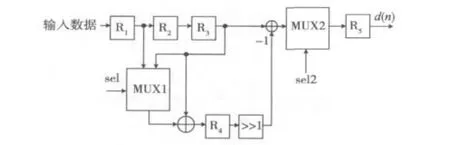
图4 行变换预测硬件实现框图

行变换更新的实现与预测基本类似。对一维提升小波变换的仿真如图5所示，其中S为输入数据，approximation表示低频分量，detail表示高频分量。

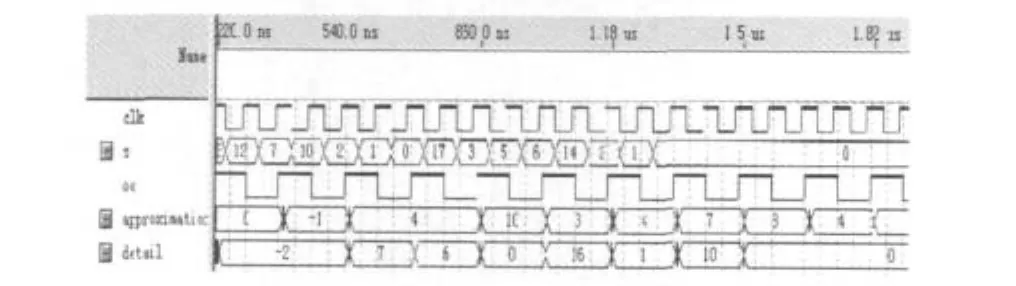
图5 一维提升小波正变换的仿真(截图)

3.2.2 二维提升小波变换的FPGA实现［8－10］

如图6所示，在一维变换的基础上，对于一幅存储在RAM2的二维图像，首先执行一维行变换，行提升小波变换完成后，再对每一列数据进行提升小波变换;列变换的方式和行变换的方式基本相同，最终的小波系数存储在RAM2中，即可完成二维提升小波正变换。将提升正变换过程中列变换和行变换模块分别用于反变换过程行方向和列方向的小波变换模块，就可以得到二维提升小波反变换。

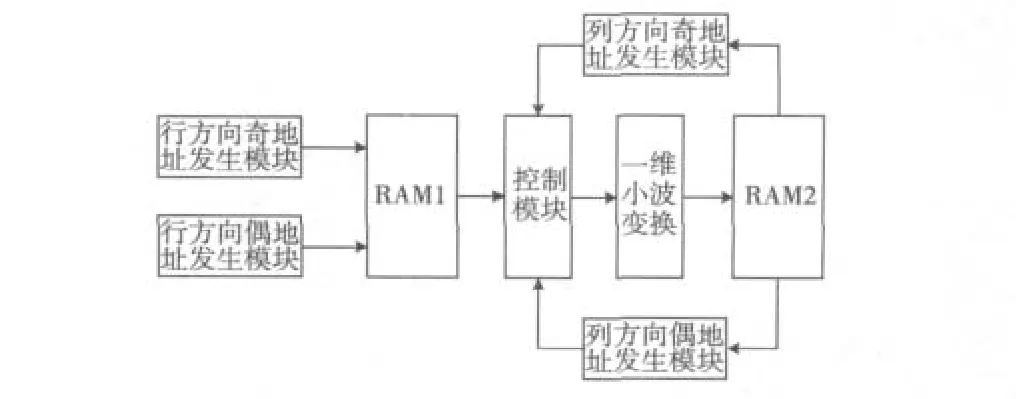
图6 二维提升小波变换的FPGA实现

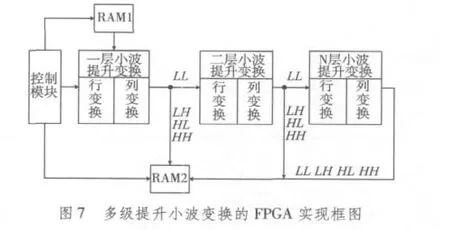
3.2.3 多层小波提升变换的实现方法

在二维提升小波变换的基础上，通过多级变换控制就可以完成多层小波二维提升变换，如图7所示。小波多级分解控制由状态机实现，状态转换如图8所示，系统复位后，提升小波变换进入S0状态，首先置当前分解级数为0，然后设置小波变换的行数、列数和分解的总级数，启动小波变换后由S0状态转向S1进行行变换，行变换结束后由S1状态转向S2进行列变换，列变换完成后当前分解级数增1，如果当前分解级数小于设定的分解总级数，由S2状态转向S1进行下一级分解，否则S2状态转向S0以结束多级小波提升分解。

4 实验结果及分析

为了验证本设计实现的有效性，选用了多光谱图像和高分辨力图像进行融合，采用了图9所示的实验方案。

图9 实验方案

1)将测试图像转换为仿真的激励信号，分别利用ModelSim软件、MATLAB软件工具进行IHS和提升小波变换图像融合，并分别记录输出的二进制图像数据。ModelSim仿真数据同MATLAB计算结果之间最大误差为3，误差为0的像素平均占95%，表明了FPGA实现了该算法。

2)利用MATLAB将1)中记录的二进制数据转换为图像信息，如图10所示，可见本文方法融合图像与软件融合结果比较接近，部分区域的模糊是由于运算过程中数值取舍误差所致。

图10 融合算法处理结果

5 结论

本文在分析IHS和提升小波变换图像融合算法原理的基础上，给出了一种基于FPGA的该图像融合算法的实现设计，重点给出了IHS变换算法分析及图像二维提升小波变换的FPGA实现，实验结果表明，该设计在误差允许的范围内，实现了融合算法的实时处理，并得到了较好的融合效果。该设计方法可以满足遥感测控微型化、时效性的需求，具有较好的应用前景。

［1］李朝锋，曾生根.遥感图像智能处理［M］.北京:电子工业出版社，2007:190－191.

［2］罗智勇，杨武年.基于梯度权重规则的IHS变换与小波变换结合算法［J］.光电工程，2007，34(10):102－107.

［3］王红梅，李言俊.一种改进的遥感图像融合方法［J］.光电工程，2007，34(7):50－53.

［4］唐国良.一种基于IHS和小波变换的彩色图像融合算法［J］.计算机应用研究，2006(10):174－176.

［5］赵高鹏.基于提升小波的红外和可见光图像融合方法［J］.计算机工程与设计，2009，30(7):1697－1699.

［6］龚建周，刘彦随，夏北成，等.IHS和小波变换结合多源遥感影像融合质量对小波分解层数的响应［J］.中国图象图形学报，2010，15(8):1269－1277.

［7］孙颖力.图像融合算法的研究及可重构FPGA实现［D］.西安:西北工业大学，2007.

［8］崔巍，汶德胜，马涛.二维提升小波变换的FPGA结构设计［J］.计算机工程，2007，33(15):261－263.

［9］薛坚.提升小波变换的应用与硬件实现［D］.南京:南京航空航天大学，2008.

［10］刘桂华，冯全源.图像的二维提升小波变换的FPGA实现［J］.电子技术应用，2008(3):108－110.