单相PWM逆变电路的两种仿真模型建立
吴炳娇,赵 峰
(兰州交通大学自动化与电气工程学院,甘肃 兰州 730070)
1 引言
PWM控制技术在电力电子技术中占有重要的地位,电力电子中各种电能变换电路的实现基本都依赖于PWM技术,尤其在逆变电路中的应用十分广泛,目前中小功率的逆变电路几乎都采用了PWM技术。PWM控制技术就是对脉冲宽度进行调制的技术,即通过对一系列脉冲的宽度进行调制,来等效地获取所需要的波形。PWM控制技术首先在逆变电路中获得应用,并且它是依赖于在逆变电路中的应用,才发展得比较成熟。PWM控制技术在电力电子中应用,得益于它能够改善相控技术给电能变换所带来的谐波等不和谐因素,使电能变换能够获得更好的应用。
2 单相桥式逆变电路
单相桥式逆变电路是三相桥式逆变电路的基础,二者的基本理论是相同的。为了说明PWM技术在逆变电路中的应用,以单相桥式逆变电路为例,对逆变电路的工作过程进行分析。开关器件可以采用各种电力电子器件,这里采用IGBT作为开关器件。图1所示为单相桥式逆变电路的框图,设负载为阻感负载。在桥式逆变电路中,桥臂的上下两个开关器件轮流导通,即工作时V1和V2通断状态互补,V3和V4的通断状态互补。为了进一步说明逆变电路的工作原理,作如下分析。如图1所示,u0为逆变输出电压。当输出电压u0为正时,V1保持通态,则根据桥式电路的原则,V2保持断态,V3和V4轮流导通。在负载电流为正的区间,V1和V4导通时,负载电压u0等于直流电压Ud;V4关断时,由于电感的作用,负载电流通过 V1和VD3续流,u0=0。由于电感的作用,如果负载很大有可能出现电感的放电情况,即在负载电流为负的区间,仍为V1和V4导通时,因i0为负,故电流实际上是通过VD1和VD4流通,仍有u0=Ud;V4关断,V3 开通后,i0从 VD1 和 V3 续流,u0=0。这样,u0总可以得到Ud和零两种电平。同样,在u0的负半周,同样可以得到-Ud和零两种电平。

图1 单相桥式PWM逆变电路
3 开关器件的通断控制方法
以双极性的PWM控制方式进行说明。通常采用调制信号和载波信号相比较形成的,调制信号ur为正弦波,载波uc为正负变化的三角波。当ur为正半周波形时,uc是为正负方向的三角波形,当ur为负半周波形时,uc仍为正负方向上的三角波形。uc与ur的交点时刻为控制IGBT的通断的时刻。由于输出的PWM波与ur为同周期的波形,因此如前所述,ur为正半周时,V1保持通态,V2保持断态,V3和V4轮流导通。ur>uc时V4导通,V3关断,获得u0=Ud,当 uc>ur时 V3 导通,V4 关断,u0=0。同理在 ur为负时,可以获得 u0=0 和 u0=-Ud。随着开关管以载波频率fc轮番导通,则逆变器输出电压u0不断在正负Ud间切换。
4 在Matlab下产生PWM控制信号的数学模型建立
在建立PWM控制信号的数学模型之前,有两个重要参数需要说明。其一为载波信号频率fc与调制信号频率fr之比,称之为载波比,可以用p来表示。正弦调制信号与三角载波信号的幅值之比可以定义为调制深度m。两个参数对输出波形的影响极大。正弦波的方程式为f(t)1=Asinwt,由于对于桥式电路,一个桥臂有上下两个电力电子器件,因此要有4个脉冲信号,又由于同一时刻同一桥臂的上下两个电力电器件不能同时导通,因此同一个桥臂的上下两个开关器件的触发脉冲互补。由于在逆变电路中负载都是阻感性负载,电流会滞后于电压,如图2所示,在产生PWM信号时,constant2 是必需的,其中 constant2 是根据 f(t)2=Asin(ωt+θ),其中 constant2 代表的就是 θ 转换为弧度值的数据。在此更正某些资料中对该问题提出方案的不妥之处,提出在控制两个桥臂的开关器件时,需要有两个桥臂上的开关器件导通的相交区间,即V1和V3,以及V2和V4的触发脉冲有一段是相交的,如图3所示。如果V1和V3,以及V2和V4的触发脉冲是V1触发区间与V3以及V2和V4的触发区间完全相同,则由于电感的作用可以使得仿真结果的输出电压和电流很小,达不到所期望的值,这个可由读者自行进行仿真检验。
5 单相桥式逆变电路在Matlab下的仿真及其分析
本文建立了两个逆变电路模型并进行了仿真,分别是直接利用Matlab下的PWM发生器,以及根据PWM由载波和调制波产生的机理自行建立的双极性PWM信号,对桥式逆变电路进行了仿真。其Matlab下的仿真模型分别如图4和图6所示,其中图3是图4中子系统的数学模型。其中两种模型的参数一致,其中调制深度p为0.5,基波频率为50Hz,调制比为15。图5所显示的波形由上到下依次为逆变输出电压、逆变输出电流、直流侧电流。图7所显示的波形由上至下与图5一致,其中图7第4部分所显示的是由“PWM Generator”产生的SPWM波。由仿真波形图5与图7可以很明显得看出两种仿真模型的输出波形是一致的。

图2 SPWM信号的Simulink产生图
图3 Simulink下建立的PWM Generator模块产生的SPWM波形图
6 结论
由以上论述可知,本文中所建立的PWM发生器的数学模型与Matlab中提供的PWM发生器,在逆变电路中的仿真波形相一致,由此可知PWM发生器数学模型的正确性。因此可以依据此处提出的建立PWM脉冲发生器的方法进行建模和相应地仿真,而且在进行模型建立时,值得注意的是上下桥臂的触发脉冲的相交区间的存在。在此问题中,建立的数学模型与PWM发生器的“look under mask”下的模型的差异还需要进一步进行分析、研究和对照,这也是下一步研究和仿真的重点。

图4 SPWM波由子系统产的单相桥式逆变电路的仿真模型图
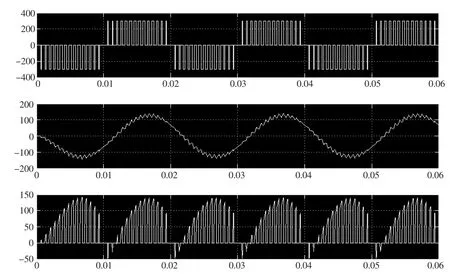
图5 SPWM波由子系统产的单相桥式逆变电路的仿真波形图

图6 PWM Generator产生PWM波的单相桥式逆变电路的仿真

图7 PWM Generator产生PWM波的单相桥式逆变电路的仿真波形图
[1]陈国呈.PWM变频调速及软开关电力变换技术[M].北京:机械工业出版社,2001.
[2]张崇巍,张 兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.
[3]MARWALI M N.Digital Control of Pulse Width Modulated Inverters for High Performance Uninterruptible Power Supplies[D].Ohio:Ohio State University,2004.
[4]BLAABJERG F,PEDERSEN J K,JAEGER U,et al.Single Current Sensor Technique in the DC Link of Threephase PWM-VS Inverters:A Review and a Novel Solution[J].IEEE Transactions on Industry Applications,1997,33(5):1241-1253.
[5]王兆安,黄 俊.电力电子技术(第4版)[M].北京:机械工业出版社,2004.
[6]赵振波,李和明,许伯强.基于虚拟磁链的PWM整流器数学模型及其仿真[J].华北电力大学学报,2003,30(1):5-9.
[7]孙向群,王久和.电压型PWM整流器功率控制策略研究[J].华北科技学院学报,2004,1(2):80-83.
[8]Depenbrock M.Direct Self-Control(DSC)of Inverter-Fed Induction Machine[J].IEEE Trans.on Power Electronics,1988,3(4):420-429.

