过饱和交通网络的多层边界主动控制方法*
李轶舜 徐建闽 王琳虹
(1.华南理工大学土木与交通学院,广东 广州510640;2.吉林大学交通学院,吉林 长春130022)
随着城市机动化进程的发展,城市交通拥堵问题日益突出.在路网中一些通行能力不足的交通瓶颈处,往往会出现排队长度无法及时消散,需要进行二次排队甚至排队溢出的过饱和交通状态.对于过饱和网络的控制,相关学者做出了很多代表性的成果.Langer和 Benekohal[1]提出了一个过饱和干道单向排队管理信号协调控制算法;Girianna[2]将该方法扩展至具有多个相交和平行道路的干道网络;Chang等[3]提出了一个利用类似Bang-Bang控制模型的过饱和动态信号控制方法;Aboudolas等[4]将过饱和网络信号设计问题建模为一个二次规划问题,试图最小化及均衡各路段排队长度,避免排队溢出.然而,上述方法都是在拥堵发生后,被动地进行疏散,这种被动的控制策略严重影响了实际的控制效果.
Gal-Tzur等[5]提出了一种将外围进入流量控制在关键交叉口通行能力之内的过饱和网络控制方法.该方法能够预防拥堵的发生.但是,该方法仅仅适用于只包含一个关键交叉口的过饱和网络,适应性大打折扣.张勇等[6]提出了一种交通网络死锁控制策略,将拥堵区路网上的累积车辆数作为状态变量,建立了拥堵区路网宏观交通流状态方程.根据庞特里亚金极小值原理求解状态方程,确定 Bang-Bang控制为最优控制策略,并使拥堵区路网累积车辆数最快达到最优合理值,从而维持路网通行能力最大.笔者[7]提出了一种边界控制方法,该方法限制进入路网的交通量,将路网维持在近饱和状态运行,与TRANSYT-7F相比,该方法能够极大地提高过饱和区域的运行效率.然而,上述方法的控制边界都是靠经验由交通工程师事先确定的,而且在堵塞区边界交叉口上控制车辆的流入可能会引起边界交叉口上游路段的排队溢出,降低边界外路网的运行效率,并扩大堵塞区的影响范围,这与缓解超饱和堵塞的目标相违背.
文中对文献[7]提出的边界控制方法进行拓展,给出了基于过饱和相邻交叉口关联度的初始研究区域确定流程,并以关键交叉口为中心,沿着拥挤扩散的方向设计多层控制边界,充分利用拥堵区内路段的存储能力,避免边界路段的排队溢出,缩小拥堵影响区范围并降低延误.
1 过饱和边界控制方法
Daganzo等[8]从理论上证明了路网上的车辆数与离开路网的交通流量呈现如图1所示的单峰型关系(城市交通网络宏观交通基本图).图1中,g为单位时间内离开路网的车辆数,γ为g的最大值,n为路网累积车辆数,˜μ和¯μ分别为路网处于最大通行能力情形下的累积车辆下限和上限.路网处于拥挤状态时,累积车辆不断增加,只要适当控制进入路网的流量,就能够使路网运行在近饱和状态,避免排队溢出甚至死锁等严重的交通拥堵发生.
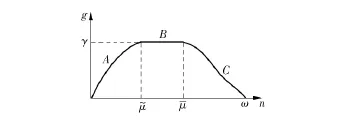
图1 城市交通网络宏观交通基本图[8]Fig.1 Macroscopic traffic flow of urban network
基于城市交通网络宏观交通基本图,文献[7]中提出了一种过饱和网络的边界控制方法,主要包括:
(1)数据清洗
当交叉口的交通需求超过了其通行能力,没有足够的绿灯时间来放行各方向到达的车辆时,某些车辆将在路段上排队等待几个周期才能够通过交叉口,极有可能形成排队溢出.因此,在过饱和情况下,某个流向(或者路段)的到达交通量是由上游交叉口的信号配时决定的,下游的交通量并不等同于实际的交通需求,而是上游交叉口的流出量.换句话说,过饱和状态下,交通量是由上游交叉口绿灯时间确定的;但是,绿灯时间的优化又基于交通量,这就产生了一个“鸡生蛋,还是蛋生鸡”的怪圈.交叉口检测到的交通量只是能够通过交叉口的交通量,并没有反应交叉口各方向的实际交通需求.文献[7]中设计了交通量清洗算法TVCA同时确定交叉口初始交通量和初始信号配时,起到数据清洗的作用,为过饱和情况下信号配时优化打下了坚实的数据基础.
(2)识别关键交叉口
Pignataro等[9]指出,城市道路交通阻塞往往是由于某些交叉口的交通需求暂时性超出其通行能力而导致阻塞在时间上与空间上扩展.严重的交通阻塞现象都是先从某些交叉口相邻路段的排队开始,逐步蔓延至上游交叉口,造成区域性拥堵的过饱和状态.这些交叉口称为过饱和网络的关键交叉口.只要将这些关键交叉口交通流量限制在其通行能力之内即可避免拥堵的扩散和恶化.文献[7]中利用改进的基于车道组的交通流模型[10],识别过饱和路网的关键交叉口,计算关键交叉口各车流需要减少的交通量.该过程也在TVCA算法中完成.
(3)最大化路网流出量
在路网交叉口处在近饱和状态且没有路段发生排队溢出时,交叉口的通行能力得到充分的利用,路网流出量最大.文献[7]中设计了TMA(Throughout Maximizing Algorithm)根据入口交通量到达关键交叉口的比例及关键交叉口需要减少的流量设计流量限制算法,确定信号周期和入口需控制进入的车辆数,并依据“饱和度均衡”原则分配绿灯时间.
(4)最小化路网延误时间
在信号周期和绿灯时间的基础上(即保证路网流出量最大化),利用遗传算法优化相序和相位差,最小化路网延误时间.
上述算法将在本文中应用,因篇幅所限,在此不再赘述,请读者查阅文献[7].
2 过饱和网络关联度
过饱和状态的定义是过饱和控制边界确定的切入点.总体而言,孤立交叉口的过饱和状态一般指到达率超过通行能力的情形,亦即绿灯结束后有排队剩余,但城市路网中很少有交叉口处于绝对孤立的状态.网络中交叉口的过饱和状态为其中至少有一个交叉口所有流向交通需求在一段时间内持续超过通行能力、发生排队溢出并阻塞关联交叉口的状态,须同时考虑相关联的多个交叉口才能有效疏解.因此,排队是判断过饱和状态的关键参数.
与文献[10]类似,文中通过检测某一时段内上游流入车辆数和下游流出车辆数,获得路段上存在的车辆数,以此来研究过饱和情况下的交叉口关联度.首先定义路段排队比为

式中:q(i-j)为研究时段内路段(i-j)存在的最大车辆数;Q(i-j)表示路段阻塞车辆数,可由路段长度L(i-j)、阻塞密度 kjam及路段车道数 n(i-j)求得,

当r(i-j)≥1时,认为该路段已经过饱和,需要进行边界流量控制.
但当需求较高或者路段长度较短时,即使路段排队比较小,由于交通需求的波动性,也存在着潜在的排队溢出危险.因此,我们根据需求的波动性,定义了路段最大可能存在车辆数,如下式所示:

式中:Kp为对应上游交叉口各相位内,能同时流向下游的车流流向,即第p相位时,能同时流向下游的车流流向,P为上游交叉口的相位数;qa为上游交叉口第 a 流入流向的流量,辆/h;γ(i-j)为路段(i- j)交通量的波动系数,该系数可由历史数据获得.
定义路段最大可能排队比为最大可能存在车辆数与路段阻塞车辆数之比:

相邻交叉口i与j之间的关联度cor(ij)可以定义为双向路段最大可能排队比的最大值:

3 过饱和网络多层边界控制方法
3.1 初始拥堵区域的确定
在进行边界控制之初,首先要确定整个拥堵范围,即交通拥堵影响区域.在路网中发生过饱和情况时,主要考虑过饱和条件下相邻交叉口之间关联度的变化.以关联度为标准,划分出阻塞区、过渡区和常态区.与文献[9]不同的是,我们认为交通拥堵状态是由阻塞源向四周扩散的过程,在过渡区中,从外围向阻塞区是拥堵的累积方向,而从阻塞区向外围是拥堵的消散方向,因此没有独立的消散区,如图2所示.阻塞区和过渡区组成初始的拥堵区域.确定该初始区域的目的是为了进行文献[7]中的数据清洗过程,避免初始区域过小,边界落在过渡区或者阻塞区,检测出的交通流量不能反应实际的交通需求;且初始区域过大则会增加建模的复杂度和计算量,影响信号配时优化的精度.
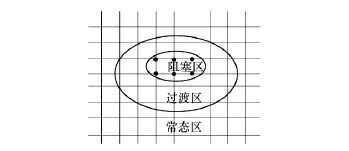
图2 过饱和区域交通状态界定Fig.2 Delimiting oversaturated area traffic state
图3为初始边界区域确定流程图.其中,N(Aa)表示集合Aa中的交叉口个数表示相邻交叉口关联度子集cor(ca)中的第j项关联度值,corcritical表示关联度的临界值.

图3 初始拥堵区域确定流程Fig.3 Flow chart of definition of initial congestion area
多层边界控制能够有效预防排队溢出,避免拥堵扩散,拥堵区域要小于没有实行控制时的拥堵区域;因此,最外层的控制边界一定落在初始的拥堵区域内,该区域满足多层边界控制的要求.
3.2 分级边界演化及控制方法
如上文所述,单一的控制边界无法充分利用边界控制区域内路段的存储能力,可能会引起边界交叉口上游路段的排队溢出,降低边界外的路网的运行效率,并扩大堵塞区的影响范围.本节中设计的多层边界控制方法,不仅能够动态的确定最优的控制范围,而且可通过多层控制,将排队分布在控制区域内的路段上,既避免了过饱和状态的发生,又避免了拥堵向外围扩散.多层边界控制方法具体步骤如下.
(1)采用TVCA算法,以3.1节确定的初始区域作为研究对象,得出关键交叉口 C1,C2,…,CI.设置一个虚拟的根节点R,将关键交叉口作为其子节点.
(2)寻找各关键交叉口的相邻交叉口,作为其子节点,所有子节点形成以该关键交叉口为中心的一层边界控制区域.若有两个或者多个关键交叉口具有相同的相邻交叉口,则将这几个一层边界控制区域合并为一个一层边界控制区域,其子节点为大的一级边界交叉口.进入边界交叉口且不在控制区域内的路段称为边界路段.令n=1.
(3)利用TMA算法优化各一层边界控制区域内交叉口的配时,控制外围进入区域的交通量,最大化区域交通流出量.
(4)利用步骤(3)所得配时执行仿真运算,获取各边界路段最大排队长度,并计算其最大可能排队比,若,令 n=n+1,转步骤(5);否则,转步骤(6).
(6)计算将上述边界路段最大可能排队长度降至阻塞排队长度时所需减少进入该路段的车辆数.
(7)固定n-1层边界区域内交叉口(包括n-1层边界交叉口)的绿灯时间,计算n层边界路段所需减少的车辆数,优化n层边界交叉口的绿灯时间,转步骤(4).
(8)利用遗传算法优化控制区域内交叉口相序和相位差,最小化路网延误,算法结束.
在步骤(6)中,由于n-1层边界区域内的交叉口交通量不会改变,因此其绿灯时间也不改变.另外,虽然在n层边界交叉口处进行了流量进入控制,进入n-1层边界路段的交通量减少,但实际上可以通过n-1层交叉口的交通量不会改变,因此配时也保持不变.
图4显示了一个具有44个交叉口的过饱和路网多层边界情况.该路网共有3个关键交叉口,两个一层边界控制区,1个二层边界控制区及1个三层边界控制区.图5是上述路网多层边界树状演化过程.


图5 过饱和路网多层边界树状演化Fig.5 Treelike evolution process of multi-layer perimeter of oversaturated network
4 案例分析
广州市天河区天河北路是一条呈东西走向的主干道,其西起广州大道北,东至五山路,全长约3.2km,共8个交叉口,9条路段,如图6所示.道路两旁有众多摩天大楼及写字楼,为广州的高级商务区,在高峰期时该路段交通流量极大,并且由于路段长度较短,极易排队溢出导致整条路段的阻塞.

图6 广州市天河北路Fig.6 Illustration of Tianhe North Road of Guangzhou
由历史数据,计算该区域相邻交叉口之间的过饱和关联度,将体育西路交叉口和五山路交叉口之间的8个交叉口作为初始研究区域.因林和西路、林和中路、林和东路、龙口西路以及龙口东路都为支路,路段较短且车道数少,存储空间较小;天寿路上游紧邻广园快速路,都不适合作为边界路段.因此,边界控制时,不限制这些路段的车辆进入路网,保证其绿灯时间.
以2011年6月3日高峰小时(17:00-18:00)的数据进行研究,包括入口的交通流量、各交叉口的转向比例及信号配时数据.数据以SCATS(Sydney Coordinated Adaptive Traffic System)交通信号控制系统的5min检测数据为基础,利用交叉口视频数据核对校准.
经过优化计算,天河北路的拥堵是由于天寿路交叉口交通需求超过通行能力而引起的拥堵扩散,即该交叉口为该拥堵区域的关键交叉口.以关键交叉口为中心,形成四层控制边界.第一层边界为与天寿路交叉口相邻的两个交叉口:体育东路交叉口和龙口西路交叉口;第二层边界为林和中路交叉口与龙口东路交叉口;第三层为林和中路交叉口和五山路交叉口.虽然经过三层边界控制后,体育西路交叉口与林和西路交叉口间路段关联度已经小于临界值,但该路段太短、排队溢出风险较大,因此将体育西路交叉口作为第四层边界交叉口.
图7(a)、(b)分别为现状、单层边界控制、多层边界控制3种情况下,天河北路东向(向东行驶)各路段和西向(向西行驶)各路段排队比.由图可以看出,在现状情况下,由于天寿路交叉口的堵塞,引起了拥堵的向上游扩散,导致上游西向多条路段排队溢出.但东向路段排队比相对较低,并没有发生排队溢出情况,这也显示了现状配时绿信比不合理.单层边界控制将超过通行能力的流量限制在外围入口,路段排队比得到了很大的降低,有效预防了过饱和现象的发生,但单层边界控制导致了车队在入口路段上的排队.虽然体育西路、体育东路、天河路以及五山路等入口路段较长,没有发生排队溢出,但排队长度很长,导致延误、停车次数和污染物排放急剧增加.多层边界控制将过剩车辆存储在各边界路段上,有效利用了各路段存储能力,缩小了拥堵区域范围,且将排队长度控制在合理水平,极大减少了延误和停车次数.

图7 3种情况下天河北路东、西向各路段排队比Fig.7 Queue ratios of eastbound and westbound links in three scenarios
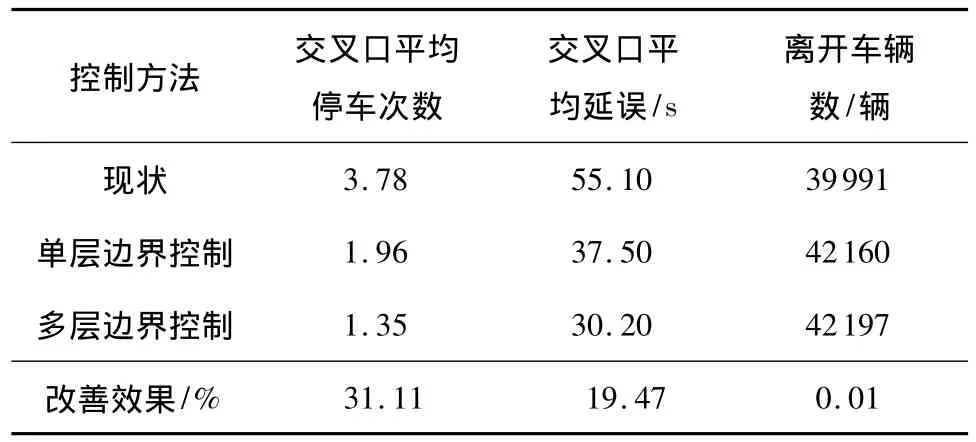
表1 3种情况下的控制效果对比Table 1 Comparison of control results in three scenarios
控制效果对比见表1,由表1可看出,两种控制策略较现状都得到了极大的优化.虽然路网的通过能力较单层边界控制变化不大,但是多层边界控制策略下交叉口平均停车次数和延误都有了较大改善.
5 结语
文中对过饱和网络单层边界控制策略进行改进,以关键交叉口为中心设计多层控制边界.案例分析表明,多层边界控制策略能够充分利用拥堵区路段的存储能力,解决单层边界控制策略边界路段排队过长甚至溢出至上游交叉口的问题,有效缩小拥堵区域范围,降低路网延误和停车次数.但相位差的优化方法还需要进行深入研究,以满足实时控制的要求,进一步降低延误.
[1]LangerAbu-lebdeh G,Benekohal R F.Development of traffic control and queue management procedures for oversaturated arterials[J].Transportation Research Record,1997,1603:119-127.
[2]Girianna M.Dynamic signal coordination models for a network with oversaturated intersections[D].Urbana-Champaign:University of Illinois at Urbana-Champaign,2002:150-177.
[3]Chang T H,Sun G Y.Modeling and optimization of an oversaturated signalized network [J].Transportation Research Part B:Methodological,2004,38(8):687-707.
[4]Aboudolas K,Papageorgiou M,Kouvelas A,et al.A rolling-horizon quadratic-programming approach to the signal control problem in large-scale congested urban road networks[J].Transportation Research Part C,2010,18(5):680-694.
[5]Gal-Tzur A,Mahalel D,Prashker N.Signal design for congested networks based on metering[J].Transportation Research Record,1993,1398:111-118.
[6]张勇,白玉,杨晓光.城市道路交通网络死锁控制策略[J].中国公路学报,2010,23(6):96-102.Zhang Yong,Bai Yu,Yang Xiao-guang.Strategy of traffic gridlock control for urban road network[J].China Journal of Highway and Transport,2010,23(6):96-102.
[7]Li Yi-shun,Xu Jian-min.Perimeter control of oversaturated network[C].∥Doctoral Forum of China 2011(Traffic Engineering).Beijing:Beijing Jiaotong University,2011:76-86.
[8]Daganzo C F,Geroliminis N.An analytical approximation for the macroscopic fundamental diagram of urban traffic[J].Transportation Research Part B:Methodological,2008,42(9):771-781.
[9]Pignataro L J,McShane W R,Crowley K W,et al.Traffic control in oversaturated street networks[C]∥Washington D C:Transportation Research Board,1978.
[10]杨晓光,黄玮,马万经.过饱和状态下交通控制小区动态划分方法[J].同济大学学报:自然科学版,2010,38(10):1450-1457.Yang Xiao-guang,Huang Wei,Ma Wan-jing.Method of delimiting urban traffic signal coordinate control subarea under oversaturated condition [J].Journal of Tongji U-niversity:Nature Science,2010,38(10):1450-1457.

